
先週は、以下のことを勉強した。

* int *a;
a EQU 0
* main()
* {
*
* *a = 1;
main
PSHS U
LEAU ,S
* generate code on type:
* list(INT)
* expr:
* list(ASS,
* list(INDIRECT,
* list(RGVAR,0)),
* list(CONST,1))
LDD #1
STD [0,Y]
* a = &a[3];
* generate code on type:
* list(POINTER,
* list(INT))
* expr:
* list(ASS,
* list(GVAR,0),
* list(ADD,
* list(RGVAR,0),
* list(CONST,6)))
LDD 0,Y
ADDD #6
STD 0,Y
* *a = *(a + a[3] + 2);
* generate code on type:
* list(INT)
* expr:
* list(ASS,
* list(INDIRECT,
* list(RGVAR,0)),
* list(RINDIRECT,
* list(ADD,
* list(ADD,
* list(MUL,
* list(RINDIRECT,
* list(ADD,
* list(RGVAR,0),
* list(CONST,6))),
* list(CONST,2)),
* list(RGVAR,0)),
* list(CONST,4))))
LDX 0,Y
LDD 6,X
ASLB
ROLA
ADDD 0,Y
PSHS D
LDD #4
PULS X
LDD D,X
STD [0,Y]
* a = *( &a + 3);
* generate code on type:
* list(POINTER,
* list(INT))
* expr:
* list(ASS,
* list(GVAR,0),
* list(RGVAR,6))
LDD 6,Y
STD 0,Y
どうして、このようなコード出力になるのかは木構造が分かってしまえば、
gexpr() をトレースするだけの問題である。この木構造は、最後の例では
単純な構文木
とは少々異なる。それは、indirect()や、rvalue() などが構文木を変換
しているからである。

&a = (int *)3; というのは、Micro-C ではエラーになる。なぜ、エラー なのかを説明せよ。
実際にコンパイラを走らせてみれば、
9:Lvalue required.
&a = (int *)3;
^
というエラー出力される。このエラーメッセージを確認しないで答えを出そうと言う
のは、少し虫が良すぎる。コードの(int *)3の部分にはエラーはない。実際、
* a = (int *)3;
* generate code on type:
* list(POINTER,
* list(INT))
* expr:
* list(ASS,
* list(GVAR,0),
* list(CONST,3))
LDD #3
STD 0,Y
という形にコンパイルされる。問題は明らかに&aの部分にある。しかし、
前の授業でも説明したように、構文的なエラーはない。このエラーは代入文
(assignemnt)に特有なエラーである。実際、Lvalue required というエラー
は、
257 (n==LVERR) ? "Lvalue required" :であり、LVERR は、expr13の&の部分と、
1363 lcheck(e)
1364 int e;
1365 { if(!scalar(type)||car(e)!=GVAR&&car(e)!=LVAR&&car(e)!=INDIRECT)
1366 error(LVERR);
1367 }
に出てくる。expr13()ではなくlcheck()でエラーになっているのはトレース
してみればすぐにわかる。この場合は、
994 expr1()
995 {int e1,e2,t,op;
996 e1=expr2();
997 switch (sym)
998 {case ASS:
999 lcheck(e1);
1000 t=type;
ここのlcheck()でエラーになるわけである。実際、lcheck では、左辺値は、
整数(scalar)か、大域変数(GVAR)か、局所変数(LVAR)か、間接参照であるとし
ている。&a は、そのどれでもないのでエラーとなる。(ANSI-C では、
この他にも、いくつか左辺値を許している。どのようなものがあるだろうか?)

これで、左辺値、右辺値ののコード生成、条件分岐やループのコード生成 を勉強したことになる。コード生成の流れを少しまとめてみたので参考に してみてほしい。 Micor-C のコード生成
あとコンパイラで問題になるのは、手続き呼び出しである。これは局所変数 (local variable)の配置とも密接に結び付いている。手続きは、引数を 持つのが普通であり、これが呼び出し側(caller)と呼び出された側(callee) を結び付ける。
Cは手続きは値渡しと呼ばれ、単に値をコピーして送る だけで良い。Pascal などは参照渡しと呼ばれ、アドレスを送る必要がある。 参照渡しならば、引数をcallee側で変更することができるので、複数の 値を返したい時になどには便利だ。しかし、Cでもアドレスを直接送れば 同じことができる。この方が実装的には美しい。が、C++ では参照渡しを 復活させてしまったようだ... 参照渡しには複雑な問題が付きまとい、 理論的にもかなりうっとうしい。しかし、プログラムの記述は簡潔に なる。見掛けを取るか、使いやすさを取るか、そういう問題かも知れない。
局所変数や引数は、手続きが終ればなくなる変数である。これらはスタック 上にとられる。スタックは、通常、CPUに特別なサポートがあり、特別な registerを使うことになっている。これでは不便なことも多いので、それを Frame Pointer というのにコピーして使うことが多い。Frame Pointerは、 単なるindex registerを使うのが普通だが、どのregisterかは固定されている のが普通である。
6809の場合は、S がsystem stackで、Uがuser stackであり、UがFrame Pointer として使われている。例えば、
* main()
* {
* int i,j;
* int (*func)();
*
* i = a[1];
main
PSHS U
LEAU ,S
LEAS -6,S
LDD 8,Y
STD -2,U
* func = (int (*)())i;
LDD -2,U
STD -6,U
* return (*func)(j);
LDD -4,U
PSHS D
LDX -6,U
JSR ,X
LEAS 2,S
* }
LEAS ,U
PULS U,PC
_3 RTS
_INITIALIZE EQU _1
_GLOBALS EQU 12
END
というような感じになる。
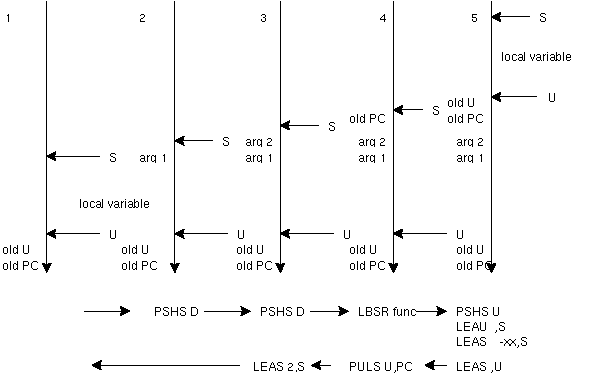
Micro-C では、手続き名の型はFNAMEであり、式を表す中間木の型はFUNCTION である。実際のコード生成はfunction()で行われる。(問題3: では、手続きの 構文解析はどこで行われているか?)
引数はスタックにつまれ、callee側ではUに対する負のオフセットを 使ってアクセスすることになる。この引数はcallerに戻る時には なくなってしまっているので、扱うことはできない。
SPARCでは、変わった呼び出し方をしている。SPARCには overraped register window というのがあり、それぞれ、%i,%l,%o というように区別されている。 それぞれ8本ずつある。call すると、caller の %o が、callee の%i となる。 これを引数渡しに使う。(したがって8個以上の引数はregister渡しにできない。 実際にはframe pointerやstack pointerがあるので、もっと少ない) また、浮動小数点には、regisger windowはない。 calleeからcallerに戻る時には、再び%iが%oとなる。これによって値を 返すことができる。この切替えは、save/restore という命令によって おこなわれる。
この方法の良いところは、stackにいちいち値をcopyしなくても済むところ である。しかし、register windowは無限にあるわけではないので、いつかは いっぱいになってしまう。その時にはsub routineを呼び出して、register windowの中身をスタックにcopyする。copyした後、戻る時には、また、スタック からregister windowにcopyする。実際のアプリケーションでは、この register window overflowが頻繁に起きるので、 残念ながら、この方法が成功しているとは いえなかったようである。
実際には以下のような呼び出しを用いる。
mov 4,%g3
call _print,0
mov %g3,%o0 callより、こちらが先に実行される
L1:
ret
restore register window をもとにもどす
.align 8
.global _print
.proc 04
_print:
!#PROLOGUE# 0
save %sp,-104,%sp register window の切替え
!#PROLOGUE# 1
st %i0,[%fp+68] %i0にcallerの%o0が入っている
sethi %hi(LC0),%o1
or %o1,%lo(LC0),%o0
ld [%fp+68],%o1
ld [%fp+68],%o2
call _printf,0 この呼び出しはregister windowを使わない
nop
L2:
ret
restore ret より先にこちらが実行される
これまでは、式(expression)単位のコンパイルを考えてきた。このコンパイルは、 直接的で簡単である。レジスタの数の少ない6809では最適に近いコードを出力 ることができる。しかし、最適化(optimize)を考える時、特にレジスタの数の 多いRISCの場合は、これではレジスタを有効利用しているとはいえない。
式の単位での最適化と、式を越えた大域的な最適化を考えるために、 基本ブロック(Basic Block)とフローグラフ(Flow Graph)というものが 工夫された。
基本単位は、単純に言えば、条件分岐や分岐を含まない逐次計算の 部分である。フローグラフは、一つの手続の中で基本ブロックを分 岐を結んだものである。
mc.c の reverse() はリストを逆順にするものだが、
484 reverse(t1)
485 int t1;
486 {int t2,t3;
487 t2=t1;
488 while(type!=t1)
489 { t3=cadr(type);
490 rplacad(type,t2);
491 t2=type;
492 type=t3;
493 }
494 type=t2;
495 }
このcadr()とかrplcad()は
2840 cadr(e)
2841 int e;
2842 { return heap[e+1];
2843 }
2894 rplacad(e,n)
2895 int e,n;
2896 { heap[e+1]=n;
2897 return e;
2898 }
である。すると、
484 reverse(t1)
485 int t1;
486 {int t2,t3;
487 t2=t1;
488 while(type!=t1)
489 { t3=heap[type+1];
490 heap[type+1]=t2;
491 t2=type;
492 type=t3;
493 }
494 type=t2;
495 }
としてよい。
このフローグラフを考えてみよう。
