Compiler Construction Lecture 11/18
Compiler Construction Lecture 11/18
先週の復習
先週は、Emulator を勉強し、コンパイラの出力の構造を調べて見た。

インタプリタとコンパイラの構造
まず、大ざっぱなインタプリタの構造を見てみよう。
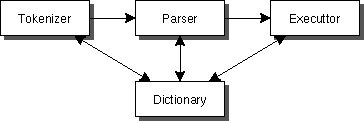
まず word (単語) の切りだしをおこなう tokenizer (字句解析)、
word から statement (文章) を作りだす parser (構文解析)、そして、
どのような文章かがわかった後に、Execution (実行) がおこなわれる。
コンパイラは実行の代わりにcode genration (コード生成)をおこなう。
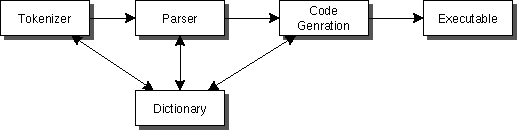
インタプリタでも最初の方法では、
例えば、loop (繰り返し)とかがあっても、その度
ごとにtokenize, parse をおこなう必要がある。これはうれしくな
い。そこで、一旦結果をintermediate code (中間コード)に落とす
ことも良く行われている。
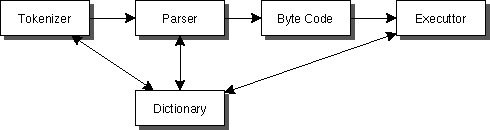
これは、実際、コンパイラとほとんど差がない。
違いは、コンパイラの作るcodeが、直接TargetのCPUが実行できる
codeになっているところである。中間コードを高機能なものに
すると、コンパイラは非常に簡単になる。
実際のコンパイラは、より複雑な構造をしている。
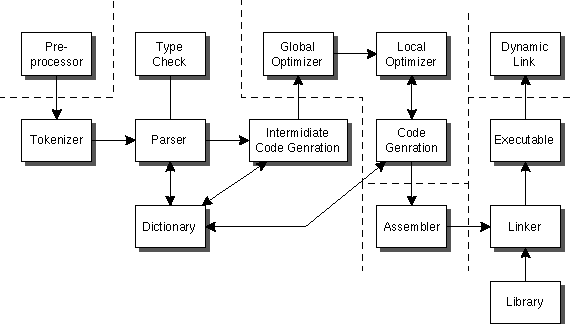
この中で、もっとも手間がかかるのはoptimizerの部分である。現在の
技術では他の部分は簡単に作成することができる。(昔は、それでも
大変だと思われていたが...) 次に手間がかかるのは、Runtime library
である。

簡単なインタプリタ
とりあえず、簡単なインタプリタを作って見よう。簡単な四則演算(+,-,*,/,>)
そして、一文字の変数(variable)への代入(assignemt)と参照(reference)
だけを持つとする。例えば、以下のような式を計算できる。
- 1
- 1+2 // expr
- 2*3
- 1+(2*3)
- 1+2*3
- 3*2-3
- 1+10*10
- (2+1030/2)-2
- (255*07)+256
- 0+(1+(2+(3+(4+(5+(6+(7+8)))))))-(0+(1+(2+(3+(4+(5+(6+(7+8))))))))
- 100/10
- a=1*3
- b=2*3
- a+b
- a=(b=3*2)
- a> 1
- b
- b> a
ここで//はcommentを表す。

Tokenizer 字句解析
まず、単語の切り分けをおこなう。 このルールは簡単で、
- 数字の続き
- 一文字の英字
- その他の記号((+,-,*,/,>)
を認識すれば良い。ここでcommentも消してしまうのが良い。字句解析を
表すのに、正規表現というのを使うこともできる。
- [0-9][0-9]*
- [a-zA-Z]
- [()=+-*/> ]
ここで[]は、その中の文字の選択、*は繰り返しを表す。あと|で複数の正規表現の
選択を表す。
Tokenizer は、通常、そのtokenの型(type)と値(value)を返す。
token.c
実際には、適当な状態遷移(state transition)を作ってやれば良い。より
複雑な例は、また、あとで見ることにしよう。
このプログラムでは、token()を呼びだすことにより以下ようにtypeとvalue
が返る。
- value 数値や変数に対応する値が入る大域変数
- last_token tokenの型が入る。token()は、この型を返す。
- 'v' ... 変数
- '0' ... 数値 (int)
- '*'など ... その他のtoken
例えば、 (2+1030/a)-2 という式は以下のように分解される。


Parser 構文解析
式の構造を考えて見れば、構文解析も簡単である。式はいくつかの
tokenのまとまりが、入れ子になった構造をしている。
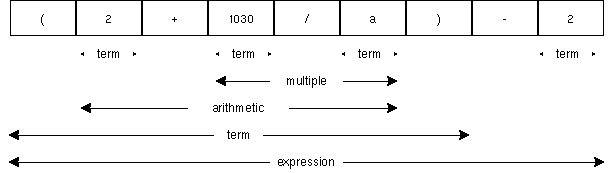
この入れ子を木で表すこともできる。途中の構造を省略した木で表すと、
以下のようになる。
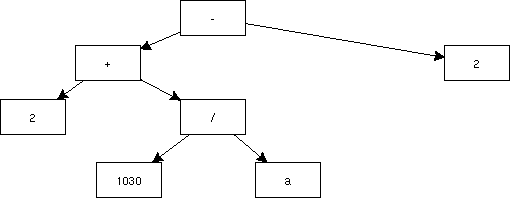
この木を見ると、この式をどのように計算していけば良いかも簡単に
わかる。木の葉から初めて、根元に向かって計算を進めていけば良いわけである。
この入れ子構造は、式を考えた時に実はruleとして既に頭の中にできている
ものである。これらのruleは、grammer rule (文法規則)と呼ばれる。grammer
を表すのに、ここでは以下のような記号を使う。
expression : arithmetic '=' expression
| arithmetic '>' expression
| arithmetic;
arithmetic : multiply '-' arithmetic
| multiply '+' arithmetic
| multiply;
multiply : term '*' multiply
| term '/' multiply;
| term;
term : VARIABLE | VALUE
| '(' expression ')';
: が入れ子構造、| が選択、; が一つのruleの終わりを表す。
例えば、multiplyは、3*4 のようなものを表す。
parser は、このルールにだいたい対応したものを作れば良い。勝手な文法
を作っても、このようなもので表されるならば、必ず、プログラムで構文解析
できることはわかっている。(このような文法はCFG context free grammar
と呼ばれている)
しかし、効率的に構文解析できるとは限らない。また、このようにして
記述された文法には曖昧さがあることもわかっている。つまり、一つの
文を複数の方法で解釈できることもある。
例えば、
この部分を手助してくれるcompiler compilerとしてyaccというのがUnixに
ある。しかし、yacc は記述された文法をすべてプログラムに変換してくれる
わけではない。また、yacc は曖昧な部分は指摘するが、勝手に解釈して
しまう。
ここでは、
手軽で、効率も良い構文解析である、Recursive Descent (再帰下降法)
というのを用いる。これは、構文規則を、再帰呼び出しをおこなう
関数に対応させる。呼びだされる規則が、その場で決まるように文法を
作れば非常に効率の良い構文解析手法となる。一般的にいって、ほとんどの
文法は、同等な決定的な文法に変換できる。しかし、Recursive Descentでは
解析できないCFGの 文法を考えることもできる。そのような文法も、
文法規則の選択のやり直しを行うことにより構文解析することができる。
しかし、それは文法を複雑にし、構文解析に必要な表や領域を拡大し、
構文解析の手間も増やしてしまう。

Execution 実行
Recursive Descent は、式の評価に向いている。何故なら再帰呼び
出しした関数が返す値を、そのまま式の値とすれば良いからである。
常に、tokenは、一つ先読みすることにする。(このように一つ先読
みを行うRecursive Descentで解析される文法をLL(1)と呼んでいる)
するとtermの部分は以下のようにすれば良い。
int
term ()
{
int d;
token(); /* token を一つ読む */
switch(last_token) {
case '0': /* 数値だったら */
d = value; /* 値は value に入っている */
token(); /* token を 一つ先読みして */
return d; /* その数値を返す。value は破壊される */
....
}
}
このtermを使ってmultiplyは、
int
mexpr()
{
int d;
d = term(); /* term をまず計算する */
switch(last_token) { /* 先読みした結果が */
case '*': /* * だったら */
d *= mexpr(); /* その先はmexprだから、それを計算して */
return d; /* それを d に掛けて、それを返す */
...
}
}
とすれば良い。文法規則とRecursive descentをおこなう手続きの対応が良くわかる。
ここで、mexprをすぐに再帰呼び出ししているが、mexpr()はすぐにterm()を
呼びだすことを考えると、mexpr()の呼び出しを一つ減らして、その代わりに
while文を増やすことでも同じことが実現できる。この方が関数呼び出しが
入らない分だけ効率が良くなる。これは、プログラム変換と呼ばれる手法の
一つである。
int
mexpr()
{
int d;
d = term(); /* term をまず計算する */
while(last_token!=EOF) {
switch(last_token) { /* 先読みした結果が */
case '*': /* * だったら */
d *= term(); /* どうせtermが呼ばれるので、それを呼びだす */
break; /* d を持って、もう一度、*があるかどうか見る */
...
}
}
}
全体のプログラムは、
s-calc.c
のようになる。
s-input.txt
に入力が用意してあるので、
% s-calc < s-input.txt | more
のように実行して見よう。

実行の様子
この方法での実行では、変数dが特殊な役割を果たしている。この変数は、
再帰呼び出しの途中での中間結果を保持していることになる。例えば、
a=2として、(2+1030/a)-2 を考えて見よう。再帰呼び出しの数だけ、
dが存在する。
d d d d d d d d
expr() ?
| aexpr() ? ?
| | mexpr() ? ? ?
( | | | term() ? ? ? ?
| | | | expr() ? ? ? ? ?
| | | | | aexpr() ? ? ? ? ? ?
| | | | | | mexpr() ? ? ? ? ? ? ?
2 | | | | | | | term() ? ? ? ? ? ? ? 2
| | | | | | | ? ? ? ? ? ? 2
+ | | | | | | aexpr() ? ? ? ? ? 2 ?
| | | | | | | mexpr() ? ? ? ? ? 2 ? ?
1030 | | | | | | | | term() ? ? ? ? ? 2 ? ? 1030
| | | | | | | | | ? ? ? ? ? 2 ? 1030
/ | | | | | | | | mexpr() ? ? ? ? ? 2 1030 ?
a | | | | | | | | | term() ? ? ? ? ? 2 1030 2
| | | | | | | | | ? ? ? ? ? 2 515
| | | | | | | | ? ? ? ? ? 517
| | | | | | | ? ? ? ? 517
| | | | | | ? ? ? 517
| | | | | ? ? 517
| | | | ? 517
)- | | aexpr() ? 517 ?
| | | mexpr() ? 517 ? ?
2 | | | | term() ? 517 ? ? 2
| | | | ? 517 ? 2
| | | ? 517 2
| | ? 515
| 515
縦棒は手続きの寿命を表す。?は、まだ値が決まっていないdである。
手続きが呼び出されるとdが一つ増えて、? が延びる。手続きが
終わると、dの値が決まり、dの列が一つ短くなる。
? を省略すれば、木をたどりながら計算をする時に「とっておく必要のある
値」がなにかがはっきりわかる。これは実際 stack をとっておく場所に
使っている。Recursive call(再帰呼び出し)自身がstackを使って実現
されているので、これはある意味では自明なことである。
(
2 2
+ 2
1030 2 1030
/ 2 1030
a 2 1030 2 =a
2 515 =1030/2
)- 517 =515+2
2 517 2
515 =517-2
これがinterpreterの行っていることの本質である。
これを手順で示すと、
(
2 2をしまう 2
+ 2
1030 1030をしまう 2 1030
/ 2 1030
a aをしまう 2 1030 2 =a
1030/2を計算 2 515 =1030/2
)- 515+2を計算 517 =515+2
2 2をしまう 517 2
517-2を計算 515 =517-2
となる。計算する所では、stackの先頭と次の値を計算している
ことの注意しよう。ここまで分解すると、そのままmachine code(機械語)
に落とせそうである。interpreterは、これを直接に実行してしまうが、
その代わりに「こうしろ」という命令を出力すれば、compiler を
作れることになる。
実際、6809の命令を使えば、
** (
LDD #2 2をload
PSHS D それをしまう
** 2+
LDD #1030 1030 をload
PSHS D それをしまう
** 1030/
LDD 0,Y a を呼びだす
LDX ,S++ stack から取り出したものをXに
EXG D,X 割り算の仕様に合わせてD,Xを交換
LBSR _DIVIDE D = D/X
ADDD ,S++ 今の値と、stackの先頭を足す。stackは一つ減る
PSHS D それをしまう
** a)-
LDD #2 2をload
SUBD ,S++ 今の値と、stackの先頭から引く
NEGA 引き算の順序が違うので負の数をとっている
NEGB
SBCA #0 これで負の数がとれた
LBSR print
となる。
問題1
以下の式を木に変換して見よ。さらに、
6809の命令に落として見よ。
- 1+(3-2)
- 0+(1+(2+3))-(0+(1+(2+3)))

宿題1
s-calc.c の若干の改良を試みる。あとでコンパイラに書き換えることを
前提にいくつかの機能をつけ加えて見よう。
- termとして8進数や16進数 (楽勝)
- -1 や -a (楽勝)
- AND(&)やOR(|)の計算 (楽勝)
- <<,>> などの算術シフト (楽勝)
- Cの三項演算子a?b:c (コンパイルは難しい)
- 配列 (宣言を別にするのが簡単だろう)
- 手続き呼び出し (入力テキストをすべて取っておく必要がある)
- 浮動小数点 (全体的な改良が必要になる。すべの数を小数点で計算するのが
楽だろう)
このうちどれかを選択し、s-calc.c を改良してcalc.cを作って見よ。
来週までに、
実行結果と、変更した主要な部分をメールにして、
Compiler Construction Lecture 11/16 のSubjectを付けて
kono@ie.u-ryukyu.ac.jp までメールすること。

prev
next
Kono's home page http://bw-www.ie.u-ryukyu.ac.jp/~kono/










