

Pure LISPとは何か?

当り前な再帰をマスタしよう。
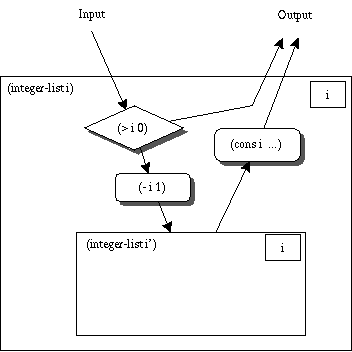
(defun integer-list (i)
(if (> i 0)
(cons i (integer-list (- i 1)))
nil))
停止条件から考える。
(defun sum-up (list)
(if (null list) 0
(+ (car list) (sum-up (cdr list)))))
listが(i) 0+i
listが(i i') 0+i+i'
...
listが(i i' ... ) (0+i+i'+ ...)

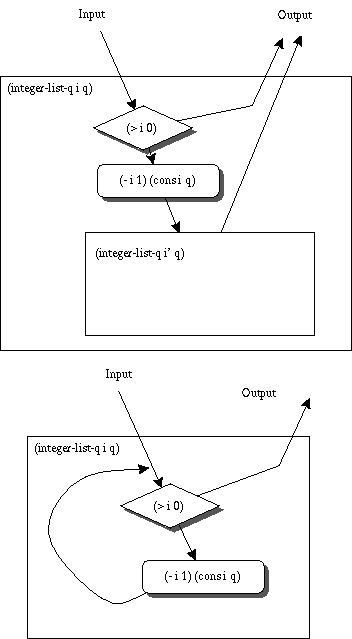
(defun integer-list-q (i q)
(if (>= i 0) (integer-list-q (- i 1) (cons i q))
q))
iとqの余分な変数がループの状態を表す。
(defun sum-up-q (list q)
(if (endp list) q
(sum-up-q (cdr list) (+ q (car list)))))
大抵の再帰は末尾再帰(tail recursion)に直すことができる。

(defun 2-times (x)
(if (endp x) nil
(cons (* 2 (car x))
(2-times (cdr x)))))
この関数の(* 2 ...)という動作をカスタマイズしたい。このような
関数は高階関数と呼ばれる。
(defun 2-time (x) (* 2 x)) (mapcar #'2-time '(1 2 3))問題: funcall と function についてinfoを調べて、mapcar と同じ働きをする 関数 my-mapcar を再帰を用いて作れ。また、その末尾再帰版 my-mapcar-q を作れ。末尾版はリストが逆順になったらreverseすれば良いということに しよう。

(defun find-assoc (key list)
(if (null list) nil
(if (eq key (car (car list))) (cdr (car list))
(find-assoc key (cdr list)))))
(defun add-assoc (key value list)
(cons (cons key value) list))
(defun remove-assoc (key list)
(if (null list) nil
(if (eq key (car (car list)))
(remove-assoc key (cdr list))
(cons (car list) (remove-assoc key (cdr list))))))
問題: addするときに重複を避ける add-assoc-uniq を作れ。

(defun tree-find (key tree)
(if (null tree) nil
(let ((here (car tree))
(left (car (cdr tree)))
(right (car (cdr (cdr tree)))))
(cond ((string< key (car here))
(tree-find key left))
((string> key (car here))
(tree-find key right))
((string= key (car (car tree)))
(cdr here))))))
let は一時変数を生成する。
(defun tree-insert (key value tree)
(if (null tree)
(list (cons key value) nil nil)
(let ((here (car tree))
(left (cadr tree))
(right (caddr tree)))
(cond ((string< key (car here))
(list here (tree-insert key value left) right))
((string> key (car here))
(list here left (tree-insert key value right)))
((string= key (car here))
(list (cons key value) left right))))))
cadr, caddr は、car/cdr の合成である。
(defun tree-walk (tree)
(if (null tree) nil
(append
(tree-walk (cadr tree)) ; left
(list (car tree)) ; here
(tree-walk (caddr tree))))) ; right
(defun tree-walk-2 (tree q)
(if (null tree) q
(tree-walk-2 (cadr tree) ; left
(cons (car tree) ; here
(tree-walk-2 (caddr tree) q))))) ; right
問題:
(setf x (tree-insert 'kono 100 nil)) (setf x (tree-insert 'yonesu 140 x)) (setf x (tree-insert 'takara 120 x)) (setf x (tree-insert 'kyan 70 x))を実行した後のxの内容を表す木をS式で表せ。また、それを分かりやすい 図で表せ。
問題: このツリーはnilがたくさん出てきてメモリ効率が良くない。 right の後ろのnilを除くことを考えよう。そのデータ形式を 使うように上のプログラムを書き換えよ。
問題: tree-insert と tree-walk-2 を使って tree-sort プログラムを 作ることができる。tree-sort を作成し、その効率を議論せよ。


