
先週は、

コンパイラ全体の中から見ると制御構造のコンパイルは、それほど大きくない。 statement()という一つの構文要素の中で閉じている。例えば、doif()では、 if文の処理をおこなう。
742 doif()
743 {int l1,l2,slfree;
744 getsym();
745 checksym(LPAR);
746 slfree=lfree;
747 bexpr(expr(),0,l1=fwdlabel());
748 lfree=slfree;
749 checksym(RPAR);
750 statement();
751 if(sym==ELSE)
752 { if (l2 = control) jmp(l2=fwdlabel());
753 fwddef(l1);
754 getsym();
755 statement();
756 if (l2) fwddef(l2);
757 }
758 else fwddef(l1);
759 }
l1=fwdlabel()というのが未来に使うラベルの生成を行っている。
ラベルの位置が決まった時点でfwddef(l1)を行う。
if文にはelse
節がある場合があり、その場合には、ラベルは二つ必要である。
(controlの役目はなにか?)
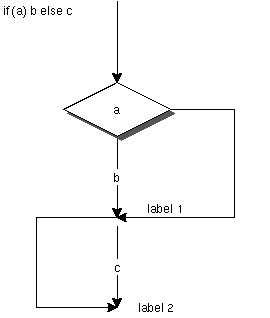

条件分岐は、構文解析はexpr()を使うが、コード生成がgexpr()とは異なり、 bexpr()により処理がおこなわれる。bexpr()は、引き数として、構文木、 条件、ラベルを取り、構文木の一番上が条件比較だったら、それお条件分岐 に書き換えている。
1560 bexpr(e1,cond,l1)
1561 int e1,l1;
1562 char cond;
1563 {int e2,l2;
1564 if (chk) return;
1565 e2=cadr(e1);
1566 switch(car(e1))
1567 {case LNOT:
1568 bexpr(e2,!cond,l1);
1569 return;
1570 case GT:
1571 rexpr(e1,l1,cond?"GT":"LE");
1572 return;
1573 case UGT:
1574 rexpr(e1,l1,cond?"HI":"LS");
1575 return;

Micro-Cの条件文のコンパイルでcontrolという変数が果たしている 役割はなにか?

これまで勉強してきた簡単なコンパイラと、C コンパイラでは、 複雑さがずいぶん違う。特に、配列(array)、構造体(struct,union)、 そして、ポインタ(pointer)をコンパイルしなくてはならない。 逆にこれらを理解して使いこなせなければCを理解していること にはならない。これらは、逆にアセンブラを通して理解する方が 容易だともいわれている。

ポインタや構造体が出て来ると、代入文も複雑になる。代入文は 以下のような構造をしている。
left value = right values-compile.c では、left value は単純(英字一文字!)だったが、 今度は配列の引数や構造体へのポインタなどを計算しなくては 代入ができない。
これらは、最終的にはload/storeの機械語に落ちるはずである。 つまり、どのアドレス(address)から、どれくらい(size)を loadして、 どれくらいをstoreするのかを決めれば良い。
Micro-C では、6809のIndex Registerを使ってaddressを計算する。 実際には、X,Y,U の3種類のポインタを使い分けている。
left valueもright valueもアドレスを計算するところまでは同じ である。そこで、Micro-C では expr はアドレスまで中間木を生成し、 必要な時にrvalue()という手続きにより値をloadする中間木を 生成している。もちろん、定数などはアドレスを計算しなくても 直接にloadされているので、rvalue() は何もしない。
ravlue() は短いが、それを理解するためには、Micro-C の中間木を 理解しなくてはならない。

2836 car(e)
2837 int e;
2838 { return heap[e];
2839 }
2840 cadr(e)
2841 int e;
2842 { return heap[e+1];
2843 }
2844 caddr(e)
2845 int e;
2846 { return heap[e+2];
2847 }
2848 cadddr(e)
2849 int e;
2850 { return heap[e+3];
2851 }
2852 list2(e1,e2)
2853 int e1,e2;
2854 {int e;
2855 e=getfree(2);
2856 heap[e]=e1;
2857 heap[e+1]=e2;
2858 return e;
2859 }
2860 list3(e1,e2,e3)
2861 int e1,e2,e3;
2862 {int e;
2863 e=getfree(3);
2864 heap[e]=e1;
2865 heap[e+1]=e2;
2866 heap[e+2]=e3;
2867 return e;
2868 }
2869 list4(e1,e2,e3,e4)
2870 int e1,e2,e3,e4;
2871 {int e;
2872 e=getfree(4);
2873 heap[e]=e1;
2874 heap[e+1]=e2;
2875 heap[e+2]=e3;
2876 heap[e+3]=e4;
2877 return e;
2878 }
2879 getfree(n)
2880 int n;
2881 {int e;
2882 switch (mode)
2883 {case GDECL: case GSDECL: case GUDECL: case GTDECL:
2884 e=gfree;
2885 gfree+=n;
2886 break;
2887 default:
2888 lfree-=n;
2889 e=lfree;
2890 }
2891 if(lfree<gfree) error(HPERR);
2892 return e;
2893 }
2894 rplacad(e,n)
2895 int e,n;
2896 { heap[e+1]=n;
2897 return e;
2898 }
これらの関数名は、LISPというLIST処理専門に設計されたプログラミング
言語から来ている。しかし、Micro-CでのLISTは、やや簡略化された
形で実装されている。本来は、list2()などは、配列ではなくLISTを
返すべきだ。これは Micro-Cでは8bit CPUつまり、64kbyteのメモリ
空間を想定しているので、LIST(2進木)を使うことによりメモリを
より多く消費することを嫌ったのだと思われる。
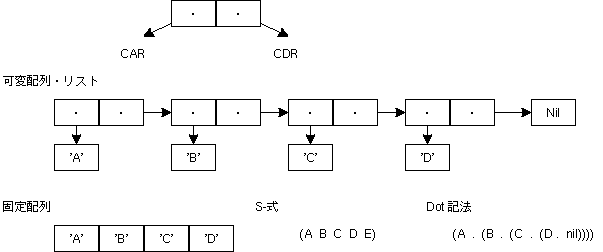
この(簡略化された)LIST(専門的にはcdr codingというのだが、 そんなことはどうでもいいことなのだが...)の、最初の要素を car()、次の要素をcadr()、次の次の要素をcaddr() という。 (最近のLISPでは、first(), second(), third() を使うのが 普通なようだ) 木には葉(leaf)と幹(node)があるのだが、 car()の値によって、それらを区別している。cadr()とかの 内容はcar()によって異なる。これはかなり複雑だが、実際には、 car()の値によって処理を変えれば良いだけだ。
どのような中間木のノードがあるかは、list2 などをgrepしてみれば 簡単にわかる。(が、かなりあるので、ここでは省略する) Micro-C では、変数の型も木で表している。したがって、式を 表す木と型を表す木の二つの木を扱うことになる。型は常に type という変数に入っている。この二種類の木は、違う構造を しているので気をつけて扱わなくてはならない。
式の方は、binop()等で生成される。ここではleft valueが生成される。 binop()はかなり複雑なので、ここには載せないことにしよう。 rvalue() は、それをright value(右辺値)に変換する。
1332 rvalue(e)
1333 int e;
1334 { if(type==CHAR)
1335 { type= INT;
1336 switch(car(e))
1337 {case GVAR:
1338 return(list2(CRGVAR,cadr(e)));
1339 case LVAR:
1340 return(list2(CRLVAR,cadr(e)));
1341 case INDIRECT:
1342 return(list2(CRINDIRECT,cadr(e)));
1343 default:return(e);
1344 }
1345 }
1346 if(!integral(type))
1347 if(car(type)==ARRAY)
1348 { type=list2(POINTER,cadr(type));
1349 if(car(e)==INDIRECT) return cadr(e);
1350 return list2(ADDRESS,e);
1351 }
1352 else if(car(type)!=POINTER) error(TYERR);
1353 switch(car(e))
1354 {case GVAR:
1355 return(list2(RGVAR,cadr(e)));
1356 case LVAR:
1357 return(list2(RLVAR,cadr(e)));
1358 case INDIRECT:
1359 return(list2(RINDIRECT,cadr(e)));
1360 default:return(e);
1361 }
1362 }
1363 lcheck(e)
1364 int e;
1365 { if(!scalar(type)||car(e)!=GVAR&&car(e)!=LVAR&&car(e)!=INDIRECT)
1366 error(LVERR);
1367 }
となっている。lcheck()は代入可能な値を表す中間木かどうかを決めている。
ここで出て来るINDIRECTとADDRESSが、Cの配列や構造体、そして、
ポインタに対応している。これらは、どういう構文で生成される
のだろうか?

Cでは、以下のポインタ演算が可能である。
1183 case MUL:
1184 getsym();
1185 e=rvalue(expr13());
1186 return(indop(e));
1187 case BAND:
1188 getsym();
1189 switch(car(e=expr13()))
1190 {case INDIRECT:
1191 e=cadr(e);
1192 break;
1193 case GVAR:
1194 case LVAR:
1195 e=list2(ADDRESS,e);
1196 break;
1197 case FNAME:
1198 return e;
1199 default:error(LVERR);
1200 }
1201 type=list2(POINTER,type);
1202 return e;
indop()では以下のように中間木を生成する。
1368 indop(e)
1369 int e;
1370 { if(type!=INT&&type!=UNSIGNED)
1371 if(car(type)==POINTER) type=cadr(type);
1372 else error(TYERR);
1373 else type= CHAR;
1374 if(car(e)==ADDRESS) return(cadr(e));
1375 return(list2(INDIRECT,e));
1376 }

array と struct は、アドレスを考えれば、統一的に扱うことができる。 例えば、a[4]というのは、a+4 というアドレスだし、a->type というのは、 a の指し示す構造体ののアドレスにtypeというoffsetを足したアドレス である。実際に、expr16()では、indop()を使ってarrayとstructの 中間木を作っている。Cから見た時には、すべてはアドレスと、その 指し示す先の大きさでしかない。大きさは型から決まる。
1312 expr16(e1)
1313 int e1;
1314 {int e2,t;
1315 while(1)
1316 if(sym==LBRA)
1317 { e1=rvalue(e1);
1318 t=type;
1319 getsym();
1320 e2=rvalue(expr0());
1321 checksym(RBRA);
1322 e1=binop(ADD,e1,e2,t,type);
1323 e1=indop(e1);
1324 }
1325 else if(sym==LPAR) e1=expr15(e1);
1326 else if(sym==PERIOD) e1=strop(e1);
1327 else if(sym==ARROW) e1=strop(indop(rvalue(e1)));
1328 else break;
1329 if(car(e1)==FNAME) type=list2(POINTER,type);
1330 return e1;
1331 }
.....
1377 strop(e)
1378 { getsym();
1379 if (sym!=IDENT||nptr->sc!=FIELD) error(TYERR);
1380 if (integral(type)||car(type)!=STRUCT && car(type)!=UNION)
1381 e=rvalue(e);
1382 type = nptr->ty;
1383 switch(car(e))
1384 {case GVAR:
1385 case LVAR:
1386 e=list2(car(e),cadr(e) + nptr->dsp);
1387 break;
1388 case INDIRECT:
1389 if(!nptr->dsp) break;
1390 e=list2(INDIRECT,list3(ADD,cadr(e),list2(CONST,nptr->dsp
)));
1391 break;
1392 default:
1393 e=list2(INDIRECT,list3(ADD,e,list2(CONST,nptr->dsp)));
1394 }
1395 getsym();
1396 return e;
1397 }

これらの中間木はgexprによってコード生成される。
1663 gexpr(e1)
1664 int e1;
1665 {int e2,e3;
1666 if (chk) return;
1667 e2 = cadr(e1);
1668 switch (car(e1))
1669 {case GVAR:
1670 leaxy(e2);
1671 return;
1672 case RGVAR:
1673 lddy(e2);
1674 return;
1675 case CRGVAR:
1676 ldby(e2);
1677 sex();
1678 return;
....
1829 case ASS: case CASS:
1830 assign(e1);
1831 return;
1832 case ASSOP: case CASSOP:
1833 assop(e1);
1834 return;
GVARがleft value、RGVARがright valuewを表している。代入文は、
さらに、assign()というコード生成手続きを呼び出す。
2014 assign(e1)
2015 int e1;
2016 {char *op;
2017 int e2,e3,e4,e5,l;
2018 op = (car(e1) == CASS ? "STB" : "STD");
2019 e3 = cadr(e2 = cadr(e1));
2020 e4 = caddr(e1);
2021 switch(car(e2))
2022 {case GVAR: case LVAR:
2023 gexpr(e4);
2024 index(op,e2);
2025 return;
2026 case INDIRECT:
2027 switch(car(e3))
2028 {case RGVAR: case RLVAR:
2029 gexpr(e4);
2030 indir(op,e3);
2031 return;
ここで、index()がSTBやSTDを生成していることが分かる。indir()では、
LDB [,X] なdが生成されて6809のindirect addressing を有効に使用
している。
binop(), assign() などは、さらに細かい処理を行っているので、 このあたりを読んで見るとcompilerの構文木の生成と、コード生成の 実際が良く分かるはずである。特にアドレスの足し算、引き算では、 特別な扱いをしていることに注意しよう。


