Compiler Construction Lecture 1/29

Compiler Construction Lecture 1/29

先週の復習

先週は、以下のことを勉強した。

手続き呼び出し



基本ブロックとフローグラフ

これまでは、式(expression)単位のコンパイルを考えてきた。このコンパイルは、 直接的で簡単である。レジスタの数の少ない6809では最適に近いコードを出力 ることができる。しかし、最適化(optimize)を考える時、特にレジスタの数の 多いRISCの場合は、これではレジスタを有効利用しているとはいえない。

式の単位での最適化と、式を越えた大域的な最適化を考えるために、 基本ブロック(Basic Block)とフローグラフ(Flow Graph)というものが 工夫された。

基本単位は、単純に言えば、条件分岐や分岐を含まない逐次計算の 部分である。フローグラフは、一つの手続の中で基本ブロックを分 岐を結んだものである。

mc.c の reverse() はリストを逆順にするものだが、 

   484	reverse(t1)
   485	int t1;
   486	{int t2,t3;
   487		t2=t1;
   488		while(type!=t1)
   489		{	t3=cadr(type);
   490			rplacad(type,t2);
   491			t2=type;
   492			type=t3;
   493		}
   494		type=t2;
   495	}
このcadr()とかrplcad()は 
  2840	cadr(e)
  2841	int e;
  2842	{	return heap[e+1];
  2843	}
  2894	rplacad(e,n)
  2895	int e,n;
  2896	{	heap[e+1]=n;
  2897		return e;
  2898	}
である。すると、 
   484	reverse(t1)
   485	int t1;
   486	{int t2,t3;
   487		t2=t1;
   488		while(type!=t1)
   489		{	t3=heap[type+1];
   490			heap[type+1]=t2;
   491			t2=type;
   492			type=t3;
   493		}
   494		type=t2;
   495	}
としてよい。

問題1

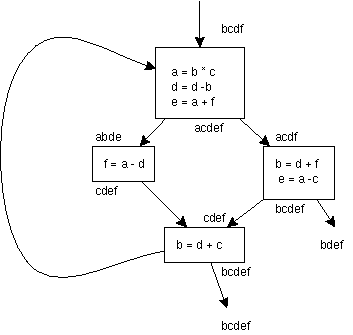
このフローグラフを考えてみよう。 このフローグラフ(flow graph)を作るには、まず基本ブロック(basic block) を抜きだす。基本ブロックは、分岐(barch)の入らない部分 のまとまりをさす。次に、flow-chart のように基本ブロックを接 続する。あと、入力される変数と、出力される変数を記述する。

flow-chart と違い、基本ブロックは最適化の単位となるので、可 能な限り一つにまとめなければならない。結果は以下のようになる。


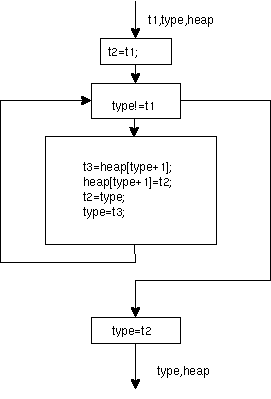
基本ブロック内部では条件分岐がないので、文(statement)の実行 順序(execution order)をプログラムの意味を変えない範囲で変更 してコンパイルして良い。これは局所的最適化と呼ばれる。

基本ブロックの間で再利用出来る式、計算する必要のない式、ある いは、使わない変数などを見つけると、それらを共有したり、削っ たりすることができる。さらに、簡単なループの場合は内部の基本 ブロックの定数などをループの外に出すことも行われる。これらは 大域的最適化と呼ばれる。これらが終わると、変数にレジスタを割 り当てる(register allocation)。RISCでは、このレジスタの割り 当て方法が重要である。



基本ブロックの最適化 Optimization of basic block

基本ブロックの最適化では共通の式などを抜きだす。このためには、 基本ブロックの中の式を一度、DAG グラフ(Directed Acyclic Graph) に直すのが良い。

DAGの作り方

前のフローグラフの真ん中のDAGは以下のようになる。

DAGからコード生成する時には、単に上から生成していくというわ けにはいかない。ちゃんと計算可能な部分から計算し、代入する時 には、他の演算がその前の値を使おうとしていないかを確かめなく てはならない。

問題 1

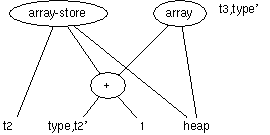
以下のプログラムのDAGを作成せよ。できれば、作成したDAGにした がってPowerPC のアセンブラを作成せよ。 

A:   a=b+c; b=a-d; c=b+c; d=a-d;
B:   a=b+c; b=b-d; c=c+d; e=b+c;
C:   e=a+b; f=e-c; g=f*d; h=a+b; i=i-c; j=i+g;
ヒント。単にグラフの形だけでなく、式の意味を考えて共通部分式と しても良い。PowerPCの命令は以下のように仮定する。 
cal     r3,r0,111      r3=111         レジスタr3に111をloadする
cal     r3,r0,r1       r3=r1          レジスタr1の値をレジスタr3にloadする、
l       r3,a(r31)      r3=a           レジスタr3にlocal variable aを代入する
st      r3,a(r31)      a=r3           レジスタr3をlocal variable aに代入する
a       a r3,r1,r2     r3=r1+r2       add 
sf[o.]  sf r3,r1,r2    r3=-r1+r2      subtract from 
muls    r3,r1,r2       r3=r1*r2       multiply



局所的最適化 Local Optimization

局所的最適化の代表的なものは peep hole optimization と呼ばれ るものである。これはいったんコードを生成した後に、そのコード を狭い範囲で見て、より良いものに置き換えられるならば置き換え るというものである。共通部分式の置き換えなどはできないが、簡 単で効果的であることが知られている。コード生成の時点で行って しまっても良い。例えば、micro-C ではそうなっている。



大域的最適化 Global Optimization

peep holeや基本ブロックの中だけの解析には限界がある。特に、 レジスタの有効利用をおこなうためには、使われない変数を探しだ し、それに割り当てたレジスタを再利用することが重要である。ま た、直前の基本ブロックで再利用出来る値があれば、それを使うこ とが望ましい。そのためには、フローグラフ上で解析を行うのが良 い。

これらの解析は大域的データフロー解析(Global dataflow analsys) と呼ばれる。まず、基本ブロックの変数の代入に番号をつける。こ の代入によって定義された値(gen)がある。一方、代入された変数 の前の値は死んでしまった(kill)。そして、基本ブロックには、入 力(in)と出力(out) がある。gen,kill,in,out は変数の代入の番号 の集合である。基本ブロックSに対して、これらの間にフロー方程 式と呼ばれる関係がある。 

out[S] = gen[S]∪(in[S] - kill[S])
この方程式を利用して、あるブロックで他のどのブロックの定数が生きている かどうかを調べよう。 
in[B] = {}          B は開始ブロック
in[S] = ∩ out[P]   P はSに先行するブロック
out[S] = gen[S]∪(in[S] - kill[S])
この方程式を繰り返してフローグラフに適用すると、いつかは変化 がなくなる。最後に得られたin[S]により、この時点での利用可能 な式がわかる。これらの演算はビット演算(and, or)を使うことが でき高速に計算することができる。

逆にoutからinを計算すると、その時点で生きている変数を調べる ことができる。ここでは、変数の使用よりも優先して確実に定義さ れる変数の集合をdef[B]、変数の定義よりも優先して使用される変 数の集合をuse[B]とする。defとする。 

in[S] = use[S]∪(out[S] - def[S]) 
out[S] = ∪ in[B]    B は後続ブロック



レジスタ割り当て Register allocation

前の方法で生きている変数がわかると、それにレジスタを割り当て ることになる。同時に生きている変数には同じレジスタを割り当て てはいけない。

このためには、変数を節点とするグラフを考える。同時に生きてい る変数を線で結ぶ。隣同士が同じ色にならないように、グラフを塗 り分けることができれば、その色がレジスタ割り当てを表している。

もちろん適当に塗り分けるのではなく、ループの中を優先するなど の努力が必要である。

問2

以下のフローグラフのレジスタ割り当てを考えてみよ。最初は手で 割り当ててみよう。