Software Engineering Lecture s01

この授業では問題は全問提出とします。すべての問題を提出してください。その代わり出席はありません。

問題は、メールでSubjectを (s01 の問題1.5ならば)

    Subject: Report on Software Engineering Lecture 1.5

として、問題毎に提出すること。

kono@ie.u-ryukyu.ac.jp まで送ること。番号のついてない問題はオプションです。

学籍番号をメールの中に記述すること。問題番号は正確に記述すること。出席しない場合でも、問題解答を送れば出席扱いとします。

提出期限は ura.ie.classes.software で知らせます。

ソフトウェアを作るということ

実際のプログラミングは、小さい例題をたくさん書けば良いと言うものではない。一人で書く短いものでも数百回も繰り返して実行されることがある。数人で書く数万行のプログラムが全世界で数億人に使われることもある。また、数百人で書いた巨大なプログラムがバグだらけで使い物にならない場合もある。

自分がプログラミングに係わることはどういうことなのかを良く考えて、その時その時で最善の努力をしよう。また、プログラミングで学ぶべきことは多い。常に、

   最新の技術から勉強する
   自分の知識を最新のものとする

ことを心がけよう。必要になったら勉強するのではなく、自分が常になんらかの分野でトップランナーであることを心がけよう。

古い技術を一つ一つ勉強するよりも、最新の技術を勉強するのに必要な知識を勉強しておく方が良い。しかし、そのためには、基本をおろそかにしてはいけない。数学的手法、論理的な方法がプログラミングの基礎であることを忘れないようしよう。

プログラムの意味

漫然とプログラムするのではなく、プログラムの意味を意識してプログラムしよう。プログラムの実行とは何か? どんなプログラムを作りたいのか? そのためには、記述すれば良いのか?

これらを整理して理解するためには、数学的手法を使う必要がある。

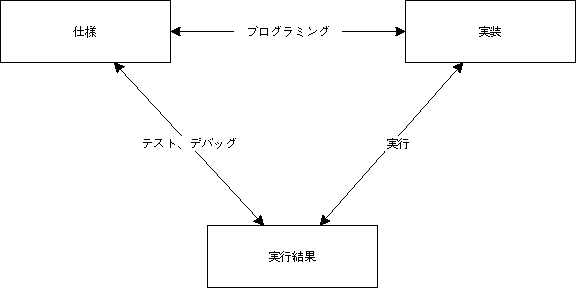
プログラムが満たしてほしい性質 ... 論理的意味、代数的意味
論理論理型プログラミング
プログラムを動かす仕組み ... 操作的意味
写像、関数関数型プログラミング
プログラムの動いた履歴 ... 実行結果
集合 Specification Z

Javaを実行して見る

Java 1.5 と、その開発環境として、Eclipse (3.1) を使用する。Java も常に最新のものを使うように心がけよう。自分は時代遅れになっていないか? 2年前の技術は既に時代遅れだ。大学生は、新しい技術を身につけて卒業して、それを広めよう。

集合

対象とするものの集まりを集合という。集合には二通りの表し方がある。

集合の要素を全部示す (外延的定義 denotation)

      { 島袋哲,上原麻乃,金城尚治,比嘉陽一,前原崇章,三野敦史,宮城尚平 }

集合が満たす性質を示す (内包的定義 connotation)
```
     {X | X は情報工学3年} 
```

有限集合を考える限りはまったく簡単だ。が、無限集合は難しい。

集合に対して簡単な演算を考えることができる。

集合演算 ... ∩ (Intersection), ∪(Union), - (Subtraction)

a ∈ A , a は集合A の要素

問題1.1

集合 D = {X | X は、メールアカウント, X は情報工学3年生}を考えよう。自分を除く5人程度の集合Dを実際に記述してみよ。

集合 E = D ∪ { X | X は自分のアカウント} を要素をすべて表示する方法で表せ。

F = {X | Xは学籍番号が奇数の人のアカウント} としよう。G = F ∩ E を求めよ。H = E - F を求めよ。

Javaの配列

もちろん、Vector とか、linked list を使っても良いが...

JavaTM 2 Platform Standard Edition 5.0 API Specification を参照にして、使えるライブラリを探そう。 for文で配列を処理するのが一般的。Iterator を使ってみよう。

	for (SelectionKey key : keys) {... }

写像、関数

何かの入力に対して決まった値を返すものが関数である。

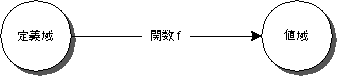
可能な入力の集合を定義域、定義域に対する出力の集合を値域という。

g 学籍番号を入力として、アカウントを出力する関数
f アカウントを入力として、名前を出力する関数
fg 学籍番号を入力として、名前を出力する関数

関数を集合と集合の対応と考える時には特に写像という言葉を用いることが多い。(その方がCの関数と混同しなくてすむし...)

二つの関数を持って来て、片方の値域と他方の定義域が適合していれば、関数の合成を作ることができる。

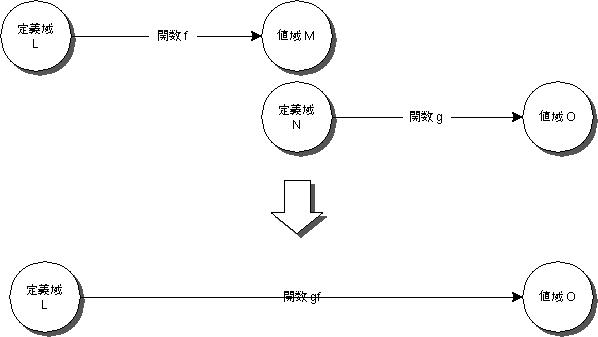
入力と出力の組み合わせの集合として関数を定義することもできる。

問題1.2

集合Dを配列に格納するJavaのプログラムを作成せよ。

fg を集合Dに対して入力と出力の組の集合を使って記述せよ。

関数fgを連想配列で実現するJavaのプログラムを作成せよ。

例題に使った関数fの定義域をEとする関数feに拡張しよう。fe 及び、fe g を集合を使って表せ。

Javaの連想配列

Map / Hashtable を使ってみよう。

    public Hashtable<Integer,String> myHash;
    myHash =  new Hashtable();

連想配列は関数として考えられるし、集合としても使うことができる。

論理

論理は以下の要素から構成される

命題 (Q,P,R) ... T / F, 正しい / 間違っている, 真 / 偽
変数 (x,y,z) ... いろいろな値が割り当てられる名前
述語 p,q(x) ... 変数を含む命題
論理演算 ... ∧ (AND), ∨ (OR), ~ (NOT)その他、論理の記号(¬,∧,⇒,⇔)を使う。

空集合をF、空でない適当な集合をT、と見ることによって、集合演算と論理演算は対応づけることができる。

A∧B	A ∩ B
A∨B	A ∪ B
¬A	T - A

集合を定義する論理式

集合を定義するのには、論理式を使うことが多い。

{X | p(X)}

述語は、T/F を返す関数を使って定義することができる。したがって、集合は、T/F を返す関数を内包的に使って定義することができる。

問題1.3

j(X) を、Xが奇数の学籍番号のアカウントであった時に真となる述語とする。h(X) を、X は情報工学3年生のアカウントであった時に真となる述語とする。集合H ( H = E -F ) を j(X), h(X) さらに、X=j99054などを含む論理式を使って表現することができる。その論理式を示せ。

集合Hを生成するJavaのプログラムを作成せよ。

具体的なプログラムに関して集合を使って意味を考える

もし入力が有限で、出力が一つだけなら、とても簡単になる。

入力が無限だったりすると難しい。特にReal-timeプログラミング、並列プログラミングの意味は難しい。

仕様は論理式で表すのが容易である
実装は関数で表すのが容易である
実行結果は集合で表すのが容易である

しかし、この三つの道具は、実際には同等な力を持った道具であり、望むならば、論理だけ、関数だけ、集合だけ、ですべてを表現することもできる。しかし、適材適所を考えて使おう。

問題1.4

有限な入力がJavaの配列として与えられ、関数がJavaのプログラムとして与えられたときに、集合を使った関数の定義を連想配列として、返す Java プログラムを作成せよ。

(ヒント: 与えられたJavaの関数の名前を決めてしまえば簡単。関数を入力として与えるのならば、関数への参照を使う)

このようなプログラムは、時間のかかる計算に対してキャッシュとしても使うことができる。そのようなキャッシュが有効なアプリケーションを一つ示せ。