Navigation

第 7 章: グラフ (graph)

7.0 グラフとは

グラフ (graph) は節点 (node, 頂点: vertex) を辺り (edge, 枝: branch) で結んだもの次のように表せる.

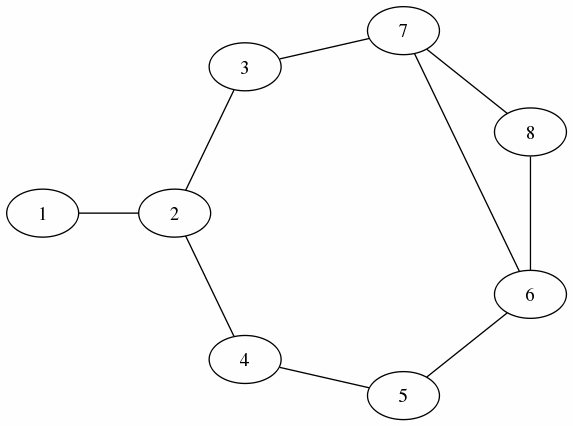
_images/dfs112.gif

隣接行列 (Adjacency Matrix) を使って, 表すと:

8 X 8 の隣接行列:
   1 2 3 4 5 6 7 8
   ---------------
1  0 1 0 0 0 0 0 0
2  1 0 1 1 0 0 0 0
3  0 1 0 0 0 0 1 0
4  0 1 0 0 1 0 0 0
5  0 0 0 1 0 1 0 0
6  0 0 0 0 1 0 1 1
7  0 0 1 0 0 1 0 1
8  0 0 0 0 0 1 1 0
  ----------------

7.1 グラフの探索 (深さ優先, DFS)

深さ優先探索:

深さ優先によりグラフのすべての節点を訪問する

深さ優先探索 (Depth First Search, 縦型探索ともいう) のアルゴリズムは次の通りである:

1. 始点を出発し, 番号の若い順に進む位置を調べ, 行けるところ (辺りで連結されていてまだ訪問していない) まで進む.
2. 行き場所がなくなったら, 行き場所があるところまで戻り, 再び行けるところまで進む.
3. 行き場所が全てなくなったら終わり (来た道を戻る)

dfs1.c

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
/*
  dfs1.c
  グラフの探索 (深さ優先)
*/

#include <stdio.h>

#define N 8 /* 点の数 */

int a[N+1][N+1] = {
  {0, 0, 0, 0, 0, 0, 0, 0, 0},
  {0, 0, 1, 0, 0, 0, 0, 0, 0},
  {0, 1, 0, 1, 1, 0, 0, 0, 0},
  {0, 0, 1, 0, 0, 0, 0, 1, 0},
  {0, 0, 1, 0, 0, 1, 0, 0, 0},
  {0, 0, 0, 0, 1, 0, 1, 0, 0},
  {0, 0, 0, 0, 0, 1, 0, 1, 1},
  {0, 0, 0, 1, 0, 0, 1, 0, 1},
  {0, 0, 0, 0, 0, 0, 1, 1, 0}
};

int v[N+1]; /* 訪問フラグ */

void
visit(int i);

int
main(int argc, char *argv[]){
  int i, j;

  /* 隣接行列を出力する */
  printf("Adjacency Matrix:\n");
  for(i = 1; i <= N; i++){
    for(j = 1; j <=N; j++){
      printf("%d ", a[i][j]);
    }
    printf("\n");
  }

  for(i = 1; i <= N; i++){
    v[i] = 0;
  }

  printf("\nOutput Graph:\n");
  visit(1);
  printf("\n");
  
  return 0;
}

void
visit(int i){
  int j;
  
  v[i] = 1;

  
  for(j = 1;j <= N; j++){
    /* 隣接行列 a[i][j] が 1 でかつ 訪問フラグ v[j] が 0 */
    if(a[i][j] == 1 && v[j] == 0){
      printf("%d->%d ", i, j);
      visit(j);
    }
  }
}

dfs1.c の実行結果は:

[wtopia 7]$ ./dfs1
Adjacency Matrix:
0 1 0 0 0 0 0 0
1 0 1 1 0 0 0 0
0 1 0 0 0 0 1 0
0 1 0 0 1 0 0 0
0 0 0 1 0 1 0 0
0 0 0 0 1 0 1 1
0 0 1 0 0 1 0 1
0 0 0 0 0 1 1 0

Output Graph:
1->2 2->3 3->7 7->6 6->5 5->4 6->8

理解を深めるために, もう一つのグラフを想定した.

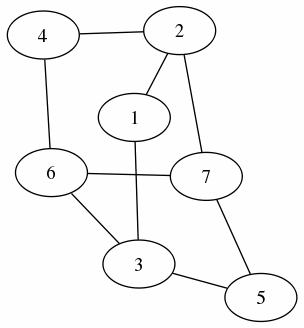
_images/dfs28.gif

隣接行列 (Adjacency Matrix) を使って, 表すと:

7 X 7 の隣接行列:
  1 2 3 4 5 6 7
  -------------
1 0 1 1 0 0 0 0
2 1 0 0 1 0 0 1
3 1 0 0 0 1 1 0
4 0 1 0 0 0 1 0
5 0 0 1 0 0 0 1
6 0 0 1 1 0 0 1
7 0 1 0 0 1 1 0
  --------------

dfs2.c

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
/*
  dfs2.c
  グラフの探索 (深さ優先)
*/

#include <stdio.h>

#define N 7 /* 点の数 */

int a[N+1][N+1] = {
  {0, 0, 0, 0, 0, 0, 0, 0},
  {0, 0, 1, 1, 0, 0, 0, 0},
  {0, 1, 0, 0, 1, 0, 0, 1},
  {0, 1, 0, 0, 0, 1, 1, 0},
  {0, 0, 1, 0, 0, 0, 1, 0},
  {0, 0, 0, 1, 0, 0, 0, 1},
  {0, 0, 0, 1, 1, 0, 0, 1},
  {0, 0, 1, 0, 0, 1, 1, 0}
};

int v[N+1]; /* 訪問フラグ */

void
visit(int i);

int
main(int argc, char *argv[]){
  int i, j;

  /* 隣接行列を出力する */
  printf("Adjacency Matrix:\n");
  for(i = 1; i <= N; i++){
    for(j = 1; j <=N; j++){
      printf("%d ", a[i][j]);
    }
    printf("\n");
  }

  for(i = 1; i <= N; i++){
    v[i] = 0;
  }

  printf("\nOutput Graph:\n");
  visit(1);
  printf("\n");
  
  return 0;
}

void
visit(int i){
  int j;
  
  v[i] = 1;
  
  for(j = 1;j <= N; j++){
    /* 隣接行列 a[i][j] が 1 でかつ 訪問フラグ v[j] が 0 */
    if(a[i][j] == 1 && v[j] == 0){
      printf("%d->%d ", i, j);
      visit(j);
    }
  }
}

dfs2.c の実行結果は:

[wtopia 7]$ ./dfs2
Adjacency Matrix:
0 1 1 0 0 0 0
1 0 0 1 0 0 1
1 0 0 0 1 1 0
0 1 0 0 0 1 0
0 0 1 0 0 0 1
0 0 1 1 0 0 1
0 1 0 0 1 1 0

Output Graph:
1->2 2->4 4->6 6->3 3->5 5->7

すべての点を始点として, そこからグラフの各節点をたどる経路を深さ優先探索で調べる.

_images/dfs112.gif

dfs3.c

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
/*
  dfs3.c
  グラフの探索 (深さ優先)
*/

#include <stdio.h>

#define N 8 /* 点の数 */

int a[N+1][N+1] = {
  {0, 0, 0, 0, 0, 0, 0, 0, 0},
  {0, 0, 1, 0, 0, 0, 0, 0, 0},
  {0, 1, 0, 1, 1, 0, 0, 0, 0},
  {0, 0, 1, 0, 0, 0, 0, 1, 0},
  {0, 0, 1, 0, 0, 1, 0, 0, 0},
  {0, 0, 0, 0, 1, 0, 1, 0, 0},
  {0, 0, 0, 0, 0, 1, 0, 1, 1},
  {0, 0, 0, 1, 0, 0, 1, 0, 1},
  {0, 0, 0, 0, 0, 0, 1, 1, 0}
};

int v[N+1]; /* 訪問フラグ */

void
visit(int i);

int
main(int argc, char *argv[]){
  int i, j, k;

  /* 隣接行列を出力する */
  printf("Adjacency Matrix:\n");
  for(i = 1; i <= N; i++){
    for(j = 1; j <=N; j++){
      printf("%d ", a[i][j]);
    }
    printf("\n");
  }

  printf("\nOutput Graph:\n");
  for(k = 1; k <= N; k++){
    for(i = 1; i <= N; i++){
      v[i] = 0;
    }
    visit(k);
    printf("\n");
  }
  
  return 0;
}

void
visit(int i){
  int j;
  
  v[i] = 1;

  
  for(j = 1;j <= N; j++){
    /* 隣接行列 a[i][j] が 1 でかつ 訪問フラグ v[j] が 0 */
    if(a[i][j] == 1 && v[j] == 0){
      printf("%d->%d ", i, j);
      visit(j);
    }
  }
}

dfs3.c の実行結果は:

[wtopia 7]$ ./dfs3
Adjacency Matrix:
0 1 0 0 0 0 0 0
1 0 1 1 0 0 0 0
0 1 0 0 0 0 1 0
0 1 0 0 1 0 0 0
0 0 0 1 0 1 0 0
0 0 0 0 1 0 1 1
0 0 1 0 0 1 0 1
0 0 0 0 0 1 1 0

Output Graph:
1->2 2->3 3->7 7->6 6->5 5->4 6->8
2->1 2->3 3->7 7->6 6->5 5->4 6->8
3->2 2->1 2->4 4->5 5->6 6->7 7->8
4->2 2->1 2->3 3->7 7->6 6->5 6->8
5->4 4->2 2->1 2->3 3->7 7->6 6->8
6->5 5->4 4->2 2->1 2->3 3->7 7->8
7->3 3->2 2->1 2->4 4->5 5->6 6->8
8->6 6->5 5->4 4->2 2->1 2->3 3->7

非連結グラフの探索:

非連結グラフを深さ優先探索で調べる
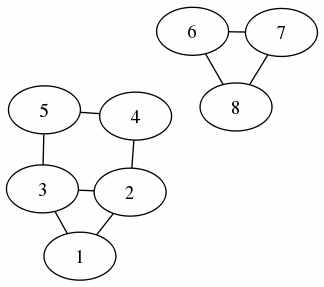
_images/dfs45.gif

dfs4.c

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
/*
  dfs4.c
  非連結グラフの探索 (深さ優先, DFS)
*/

#include <stdio.h>

#define N 8 /* 点の数 */

int a[N+1][N+1] = {
  {0, 0, 0, 0, 0, 0, 0, 0, 0},
  {0, 0, 1, 1, 0, 0, 0, 0, 0},
  {0, 1, 0, 1, 1, 0, 0, 0, 0},
  {0, 1, 1, 0, 0, 1, 0, 0, 0},
  {0, 0, 1, 0, 0, 1, 0, 0, 0},
  {0, 0, 0, 1, 1, 0, 0, 0, 0},
  {0, 0, 0, 0, 0, 0, 0, 1, 1},
  {0, 0, 0, 0, 0, 0, 1, 0, 1},
  {0, 0, 0, 0, 0, 0, 1, 1, 0}
};

int v[N+1]; /* 訪問フラグ */

void
visit(int i);

int
main(int argc, char *argv[]){
  int i, j;
  int count = 1; /* 連結成分のカウント用 */

  /* 隣接行列を出力する */
  printf("Adjacency Matrix:\n");
  printf("count = %d\n", count);
  for(i = 1; i <= N; i++){
    for(j = 1; j <= N; j++){
      printf("%d ", a[i][j]);
    }
    printf("\n");
  }

  /* 各節点のフラグを 0 に初期化する, 未訪問 */
  for(i = 1; i <= N; i++){
    v[i] = 0;
  }

  printf("\nOutput Graph:\n");
  for(i = 1; i <= N; i++){
    if(v[i] != 1){
      printf("%d: ", count++); /* count++ と ++count に変換して, 違う結果が出る */
      visit(i);
      printf("\n");
    }
  }
  
  return 0;
}

void
visit(int i){
  int j;

  printf("%d ", i);
  v[i] = 1;
  for(j = 1; j <= N; j++){
    /* 隣接行列 a[i][j] が 1 でかつ 訪問フラグ v[j] が 0 */
    if(a[i][j] == 1 && v[j] == 0){
      visit(j);
    }
  }
}

dfs4.c の実行結果は:

[wtopia 7]$ ./dfs4
Adjacency Matrix:
count = 1
0 1 1 0 0 0 0 0
1 0 1 1 0 0 0 0
1 1 0 0 1 0 0 0
0 1 0 0 1 0 0 0
0 0 1 1 0 0 0 0
0 0 0 0 0 0 1 1
0 0 0 0 0 1 0 1
0 0 0 0 0 1 1 0

Output Graph:
1: 1 2 3 5 4
2: 6 7 8

7.2 グラフの探索 (幅優先, BFS)

幅優先探索:

幅優先によりグラフのすべての節点を訪問する

幅優先探索 (Breadth First Search: 横型探索ともいう) のアルゴリズムは次の通りである:

1. 始点をキュー (待ち行列) にいれる.
2. キューから節点を取り出し, その節点に連結している未訪問の節点をすべてキューにいれる.
3. キューが空になるまで繰り返す.
_images/bfs14.gif

bfs1.c

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
/*
  bfs1.c
  グラフの探索 (幅優先探索には, キューによる実装)
  注意: キューの実装は 1 次元配列によって作られる
*/

#include <stdio.h>

#define N 8 /* 点の数 */

/* 隣接行列 8 x 8 */
int a[N+1][N+1] = {
  {0, 0, 0, 0, 0, 0, 0, 0, 0},
  {0, 0, 1, 0, 0, 0, 0, 0, 0},
  {0, 1, 0, 1, 1, 1, 0, 0, 0},
  {0, 0, 1, 0, 0, 0, 0, 1, 0},
  {0, 0, 1, 0, 0, 0, 0, 0, 0},
  {0, 0, 1, 0, 0, 0, 1, 0, 0},
  {0, 0, 0, 0, 0, 1, 0, 1, 1},
  {0, 0, 0, 1, 0, 0, 1, 0, 1},
  {0, 0, 0, 0, 0, 0, 1, 1, 0}
};

int v[N+1]; /* 訪問フラグ */

int queue[100]; /* キュー */
int head = 0; /* 先頭データのインデックス */
int tail = 0; /* 終端データのインデックス */

int
main(int argc, char *argv[]){

  int i, j;
  for(i = 1; i <= N; i++){
    v[i] = 0;
  }

  queue[tail++] = 1;
  v[1] = 1;

  do{
    i = queue[head++]; /* キューから取り出す */
    for(j = 1; j <= N; j++){
      if( a[i][j] == 1 && v[j] == 0 ){
	printf("%d->%d ", i, j);
	queue[tail++] = j; /* キューに入れる */
	v[j] = 1;
      }
    }
  }while( head != tail);

  printf("\n");
  
  return 0;
}

bfs1.c の実行結果は:

[wtopia 7]$ ./bfs1
1->2 2->3 2->4 2->5 3->7 5->6 7->8

すべての点を始点にした探索:

すべての節点を始点として, そこからグラフの各節点をたどる経路を幅優先探索で調べる.
_images/bfs14.gif

bfs2.c

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
/*
  bfs2.c
  グラフの探索 (幅優先探索には, キューによる実装)
  注意: キューの実装は 1 次元配列によって作られる
*/

#include <stdio.h>

#define N 8 /* 点の数 */

/* 隣接行列 8 x 8 */
int a[N+1][N+1] = {
  {0, 0, 0, 0, 0, 0, 0, 0, 0},
  {0, 0, 1, 0, 0, 0, 0, 0, 0},
  {0, 1, 0, 1, 1, 1, 0, 0, 0},
  {0, 0, 1, 0, 0, 0, 0, 1, 0},
  {0, 0, 1, 0, 0, 0, 0, 0, 0},
  {0, 0, 1, 0, 0, 0, 1, 0, 0},
  {0, 0, 0, 0, 0, 1, 0, 1, 1},
  {0, 0, 0, 1, 0, 0, 1, 0, 1},
  {0, 0, 0, 0, 0, 0, 1, 1, 0}
};

int v[N+1]; /* 訪問フラグ */

int queue[100]; /* キュー */
int head; /* 先頭データのインデックス */
int tail; /* 終端データのインデックス */

int
main(int argc, char *argv[]){

  int i, j, p;
  
  for(p = 1; p <= N; p++){
    for(i = 1; i <= N; i++){
      v[i] = 0;
    }

    head = 0;
    tail = 0;

    queue[tail++] = p;
    v[p] = 1;

    do{
      i = queue[head++]; /* キューから取り出す */
      for(j = 1; j <= N; j++){
	if( a[i][j] == 1 && v[j] == 0 ){
	  printf("%d->%d ", i, j);
	  queue[tail++] = j; /* キューに入れる */
	  v[j] = 1;
	}
      }
    }while( head != tail);

    printf("\n");
  }
  
  return 0;
}

bfs2.c の実行結果は:

[wtopia 7]$ ./bfs2
1->2 2->3 2->4 2->5 3->7 5->6 7->8
2->1 2->3 2->4 2->5 3->7 5->6 7->8
3->2 3->7 2->1 2->4 2->5 7->6 7->8
4->2 2->1 2->3 2->5 3->7 5->6 7->8
5->2 5->6 2->1 2->3 2->4 6->7 6->8
6->5 6->7 6->8 5->2 7->3 2->1 2->4
7->3 7->6 7->8 3->2 6->5 2->1 2->4
8->6 8->7 6->5 7->3 5->2 2->1 2->4

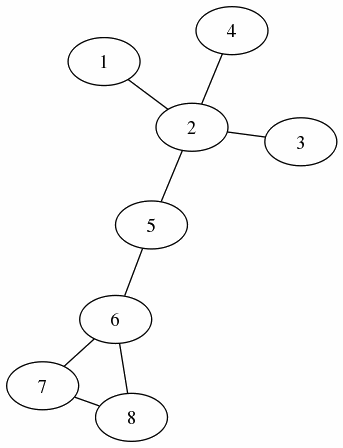
7.3 トポロジカル•ソート

1 ~ 8 までの仕事があったとする. 1 の仕事をするには 2 の仕事ができていなければならない. 3 の仕事をするためには 1 の仕事ができていなければならない. 7 の仕事をするためには, 3, 6, 8 の仕事ができていなければならない. etc という関係を有向グラフを用いると次のように表現できる

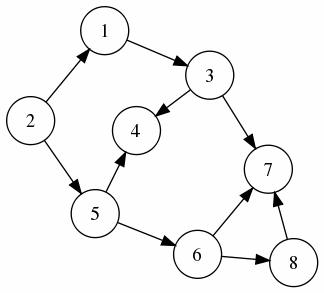
_images/topological_sort3.gif

トポロジカル•ソートは有向グラフに対し深さ優先の探索 (DFS) を行い, 行き着いたところから探索経路を戻るときに節点を拾っていけばよい

topological_sort.c

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
/*
  topological_sort.c
  深さ優先探索 (DFS) によるトポロジカル•ソート
  与えられたグラフは半順序関係
*/

#include <stdio.h>

#define N 8 /* 点の数 */

/* 隣接行列 8 x 8 */
int a[N+1][N+1] = {
  {0, 0, 0, 0, 0, 0, 0, 0, 0},
  {0, 0, 0, 1, 0, 0, 0, 0, 0},
  {0, 1, 0, 0, 0, 1, 0, 0, 0},
  {0, 0, 0, 0, 1, 0, 0, 1, 0},
  {0, 0, 0, 0, 0, 0, 0, 0, 0},
  {0, 0, 0, 0, 1, 0, 1, 0, 0},
  {0, 0, 0, 0, 0, 0, 0, 1, 1},
  {0, 0, 0, 0, 0, 0, 0, 0, 0},
  {0, 0, 0, 0, 0, 0, 0, 1, 0}
};

int v[N+1]; /* 訪問フラグ */

void
visit(int i);

int
main(int argc, char *argv[]){

  int i;

  for(i = 1; i <= N; i++){
    v[i] = 0;
  }

  for(i = 1; i <= N; i++){
    if(v[i] == 0){
      visit(i);
    }
  }
  printf("\n");
  return 0;
}

void
visit(int i){
  int j;
  v[i] = 1;
  
  for(j = 1; j <= N; j++){
    if( a[i][j] == 1 && v[j] == 0 ){
      visit(j);
    }
  }
  printf("%d ", i);
}

topological_sort.c の実行結果は:

[wtopia 7]$ ./topological_sort
4 7 3 1 8 6 5 2 (逆順を取る, 解になる)

注意:

トポロジカル•ソートの解は一つに限らないので, 複数存在する

同じような問題を tsort で解いてみた. tsort の２つの使い方がある:

1. EOF
2. file.txt

EOF の使い方は下のようになる:

[wtopia 7]$ tsort << EOF
> 1 3
> 2 1
> 2 5
> 3 4
> 3 7
> 5 4
> 5 6
> 6 7
> 6 8
> 8 7
> EOF
2
1
5
3
6
4
8
7

グラフを表すデータを tsort1.txt に保存して, tsort による解き方は下のようになる:

tsort1.txt

1 3
2 1
2 5
3 4
3 7
5 4
5 6
6 7
6 8
8 7

tsort.txt の実行結果は:

[wtopia 7]$ tsort tsort1.txt
2
1
5
3
6
4
8
7

7.4 Euler の一筆書き

7.5 最短路問題

Table Of Contents

Previous topic

第 6 章: 木 (tree)

Next topic

第 8 章: グラフィックス

Navigation

© Copyright 2010, WTOPIA.