隣接行列¶
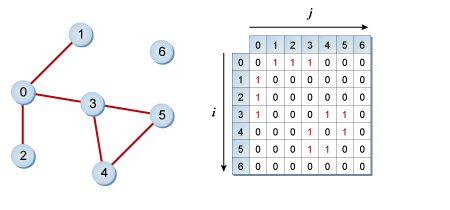
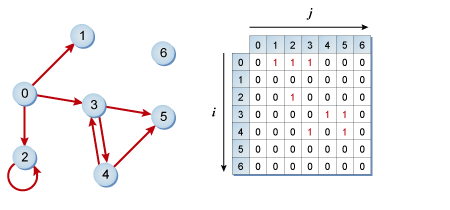
行列という名の通り, グラフを 2 次元配列で表現する. 配列のインデックスがノードの番号に対応する. 例えば, この 2 次元配列を M とすると, M[i][j] がノード i と ノード j の関係を表す.
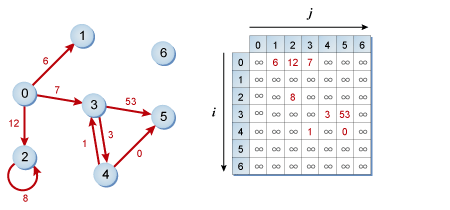
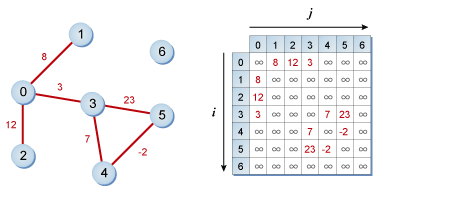
重み付き無向グラフ¶
ノード i とノード j の間に重さ w のエッジがある場合, M[i][j] と M[j][i] の値を w とする.
エッジがない場合は, 問題上あり得ない値に設定する. 例では ∞ としているが, プログラムは非常に大きな値に設定しておくと便利な場合が多い.
隣接行列表現の特徴¶
M[i][j] でエッジを参照できるので, ノード i と ノード j の関係を定数時間でチェックすることができる.
エッジの追加や削除が簡単かつ効率的 (定数時間)
ノードの数が増えるとメモリをかなり消費する. ノード数を n とすると, n^2 のスペースが必要.