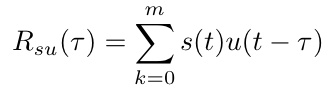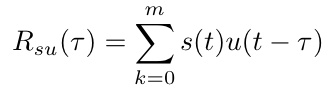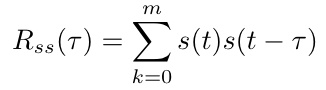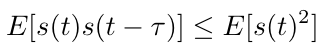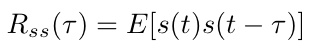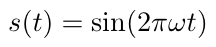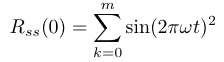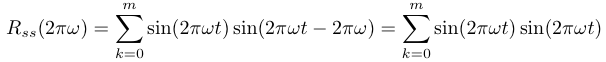2007/05/27更新

自己相関関数

ここでは、自己相関関数について説明します。

用語・記号説明

tを時刻として、ある離散時間信号s(t)に対して、1サンプルずつディレイ(delay：遅延)を加えていくと、
s(t-1),s(t-2),s(t-3),...,s(t-n),...
という信号になる。
つまり、s(t-n)という信号はある時刻tよりもnサンプル前の信号という意味である。

相互相関(cross correlation)と自己相関(Autocorrelation)

ある信号s(t)と、別の信号u(t)があるとする。これらの信号は実関数(出力が実数である関数)であるとする。このとき、
u(t)をτサンプル遅れさせたものとs(t)との各サンプルの積の総和R_su(τ)は

となる。
これをs(t)とu(t)の相互相関関数と呼ぶ。

また、s(t)とs(t)自身の相互相関関数は、とくに自己相関関数と呼び、以下の式で定義できる。

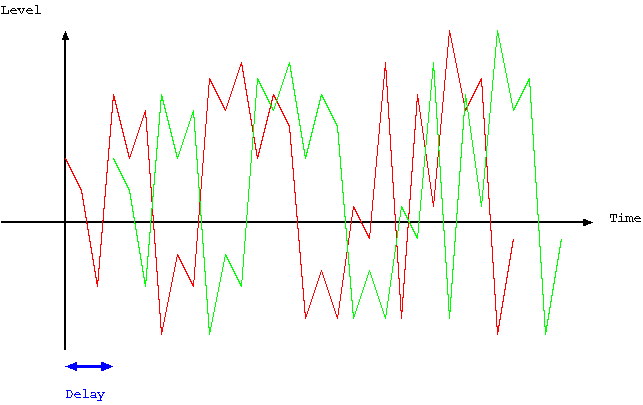
図を用いて表現すると、以下のような重ね合わせ方になる。

この図の青い矢印が信号の遅延、すなわちτを表している。
注意すべきことは、s(t)は実関数であるので、s(t)とs(t)の積は必ず正値になるということである。
ここで、s(t)とs(t-τ)の積は、τ≠0のとき、負値もあり得ることを考える。
また、たとえs(t)が常に正値である場合でも、相加・相乗平均の関係から以下の式が成り立つことが分かる。

E[]は期待値(Expectation)を表す。
有限時間信号においては積の総和を取り、無限時間信号においては以下の式で自己相関が定義できる。

適用例

信号処理において、離散時間信号の自己相関をとる事は非常に有意義である。
もしもその信号が周期性を持つならば、あるτの時にピークを示すからである。

例えば、s(t)を単純な周期関数であるsin(2πωt)とおく。

上のように定義し、τ=0のときの自己相関は

となる。ここで、τ=2πωとした場合も、

となって、等しく、τ=2πωでピークが現れる。
τ=0の時に確率的に最も大きな値をとることと、周期性のある関数では、周期と等しいτでs(t)=s(t-τ)になることから、この関数の周期を推定することができる。
すなわち、次に現れるピークを示すτが周期である。

この性質を利用して、ピッチ検出などを簡単に行なうことができる。