Compiler Construction Lecture No.4
Menu
インタプリタとコンパイラの構造
まず、大ざっぱなインタプリタの構造を見てみよう。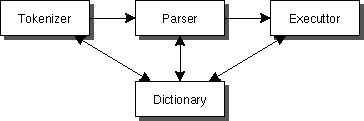
まず word (単語) の切りだしをおこなう tokenizer (字句解析)、word から statement (文章) を作りだす parser (構文解析)、そして、どのような文章かがわかった後に、Execution (実行) がおこなわれる。
コンパイラは実行の代わりにcode genration (コード生成)をおこなう。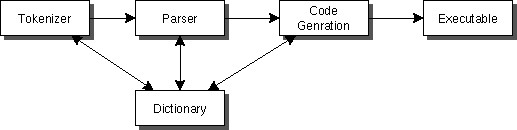
インタプリタでも最初の方法では、例えば、loop (繰り返し)とかがあっても、その度ごとにtokenize, parse をおこなう必要がある。これはうれしくない。そこで、一旦結果をintermediate code (中間コード)に落とすことも良く行われている。
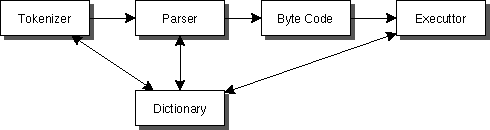
これは、実際、コンパイラとほとんど差がない。違いは、コンパイラの作るcodeが、直接TargetのCPUが実行できるcodeになっているところである。中間コードを高機能なものにすると、コンパイラは非常に簡単になる。
実際のコンパイラは、より複雑な構造をしてい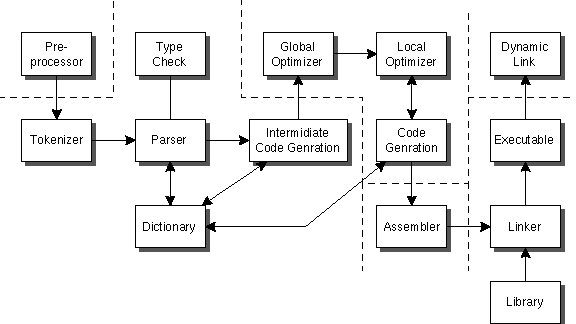る。
この中で、もっとも手間がかかるのはoptimizerの部分である。現在の技術では他の部分は簡単に作成することができる。(昔は、それでも大変だと思われていたが...) 次に手間がかかるのは、Runtime library
である。
簡単なインタプリタ
とりあえず、簡単なインタプリタを作って見よう。簡単な四則演算(+,-,*,/,>)そして、一文字の変数(variable)への代入(assignemt)と参照(reference)だけを持つとする。例えば、以下のような式を計算できる。- 1
- 1+2 // expr
- 2*3
- 1+(2*3)
- 1+2*3
- 3*2-3
- 1+10*10
- (2+1030/2)-2
- (255*07)+256
- 0+(1+(2+(3+(4+(5+(6+(7+8)))))))-(0+(1+(2+(3+(4+(5+(6+(7+8))))))))
- 100/10
- a=1*3
- b=2*3
- a+b
- a=(b=3*2)
- a> 1
- b
- b> a
Tokenizer 字句解析
まず、単語の切り分けをおこなう。 このルールは簡単で、- 数字の続き
- 一文字の英字
- その他の記号((+,-,*,/,>)
- [0-9][0-9]*
- [a-zA-Z]
- [()=+-*/>]
Perl で、実際に、これらの正規表現が前の式から、どのように字句を切りだしてくるか調べて見よう。
while(<>) {
chop;
while ($_ ne '') {
s=//.*$==;
if (s/^[0-9][0-9]*//) {
print "$&\n";
} elsif (s/^[a-zA-Z]//) {
print "$&\n";
} elsif (s/^\s//) {
} elsif (s/.//) {
print "$&\n";
}
}
}
Tokenizer は、通常、そのtokenの型(type)と値(value)を返す。プログラムは、 s-compiler.h と
s-token.c
ような感じになる。
実際には、適当な状態遷移(state transition)を作ってやれば良い。より複雑な例は、また、あとで見ることにしよう。
このプログラムでは、token()を呼びだすことにより以下ようにtypeとvalue が返る。
- value 数値や変数に対応する値が入る大域変数
- last_token tokenの型が入る。token()は、この型を返す。
- 'v' ... 変数
- '0' ... 数値 (int)
- '*'など ... その他のtoken
例えば、 (2+1030/a)-2 という式は以下のように分解される。
実装は、 s-token.c ようになる。
Automaton
このような単純なループと状態の記録で文字列の判定を行うプログラムは Automaton と呼ばれる。Parser 構文解析
式の構造を考えて見れば、構文解析も簡単である。式はいくつかのtokenのまとまりが、入れ子になった構造をしている。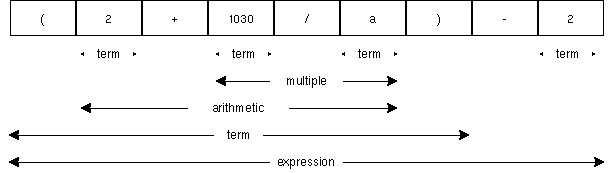
この入れ子を木で表すこともできる。途中の構造を省略した木で表すと、以下のようになる。
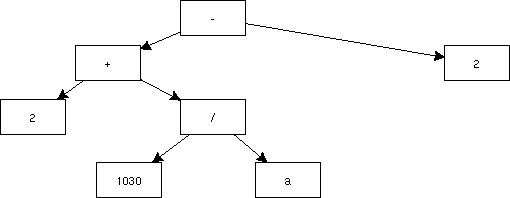この木を見ると、この式をどのように計算していけば良いかも簡単にわかる。木の葉から初めて、根元に向かって計算を進めていけば良いわけである。
この入れ子構造は、式を考えた時に実はruleとして既に頭の中にできているものである。これらのruleは、grammer rule (文法規則)と呼ばれる。grammer を表すのに、ここでは以下のような記号を使う。
expression : arithmetic '=' expression
| arithmetic '>' expression
| arithmetic;
arithmetic : multiply '-' arithmetic
| multiply '+' arithmetic
| multiply;
multiply : term '*' multiply
| term '/' multiply;
| term;
term : VARIABLE | VALUE
| '(' expression ')';
: が入れ子構造、| が選択、; が一つのruleの終わりを表す。例えば、multiplyは、3*4 のようなものを表す。
この文法だと、2/3/4 は、2/(3/4) と解釈される。これは、おかしい。でも、ここでは、これを採用することにする。
parser は、このルールにだいたい対応したものを作れば良い。勝手な文法を作っても、このようなもので表されるならば、必ず、プログラムで構文解析できることはわかっている。(このような文法はCFG context free grammar と呼ばれている)しかし、効率的に構文解析できるとは限らない。また、このようにして記述された文法には曖昧さがあることもわかっている。つまり、一つの文を複数の方法で解釈できることもある。例えば、この部分を手助してくれるcompiler compilerとしてyaccというのがUnixにある。しかし、yacc は記述された文法をすべてプログラムに変換してくれるわけではない。また、yacc は曖昧な部分は指摘するが、勝手に解釈してしまう。
ここでは、手軽で、効率も良い構文解析である、Recursive Descent (再帰下降法)というのを用いる。これは、構文規則を、再帰呼び出しをおこなう関数に対応させる。呼びだされる規則が、その場で決まるように文法を作れば非常に効率の良い構文解析手法となる。一般的にいって、ほとんどの文法は、同等な決定的な文法に変換できる。しかし、Recursive Descentでは解析できないCFGの 文法を考えることもできる。そのような文法も、文法規則の選択のやり直しを行うことにより構文解析することができる。しかし、それは文法を複雑にし、構文解析に必要な表や領域を拡大し、構文解析の手間も増やしてしまう。
Execution 実行
Recursive Descent は、式の評価に向いている。何故なら再帰呼び出しした関数が返す値を、そのまま式の値とすれば良いからである。常に、tokenは、一つ先読みすることにする。(このように一つ先読みを行うRecursive Descentで解析される文法をLL(1)と呼んでいる)するとtermの部分は以下のようにすれば良い。
int
term ()
{
int d;
token(); /* token を一つ読む */
switch(last_token) {
case '0': /* 数値だったら */
d = value; /* 値は value に入っている */
token(); /* token を 一つ先読みして */
return d; /* その数値を返す。value は破壊される */
....
}
}
このtermを使ってmultiplyは、
int
mexpr()
{
int d;
d = term(); /* term をまず計算する */
switch(last_token) { /* 先読みした結果が */
case '*': /* * だったら */
d *= mexpr(); /* その先はmexprだから、それを計算して */
return d; /* それを d に掛けて、それを返す */
...
}
}
とすれば良い。文法規則とRecursive descentをおこなう手続きの対応が良くわかる。
mexpr : term '*' mexpr;
と言う規則に mexpr() が直接的に対応する。
このように実装して、正しい結果が得られるかどうか調べよう。
s-calc-r.c s-input.txt に入力が用意してあるので、
% s-calc < s-input.txt | more
のように実行して見よう。
2-3-4
96/12/3
は、どのように計算されるだろうか?
左再帰
でも、2/3/4 が (2/3)/4 と解釈されるためには、
mexpr : mexpr '*' term;
でも、これを直接、Recursive descent で手続きに対応させると、
int
mexpr()
{
int d;
d = mexpr(); /* mexpr をまず計算する (あれ?) */
switch(last_token) { /* 先読みした結果が */
case '*': /* * だったら */
d *= term(); /* その先はmexprだから、それを計算して */
return d; /* それを d に掛けて、それを返す */
...
}
}
ここで、mexprをすぐに再帰呼び出ししているが、これでは無限ループになってしまう。これはまずい。これを、左再帰の問題と言う。
mexpr()はすぐにterm()を呼びだすことを考えると、mexpr()の呼び出しを一つ減らして、その代わりにwhile文を増やすことでも同じことが実現できる。この方が関数呼び出しが入らない分だけ効率が良くなる。これは、プログラム変換と呼ばれる手法の一つである。
int
mexpr()
{
int d;
d = term(); /* term をまず計算する */
while(last_token!=EOF) {
switch(last_token) { /* 先読みした結果が */
case '*': /* * だったら */
d *= term(); /* どうせtermが呼ばれるので、それを呼びだす */
break; /* d を持って、もう一度、*があるかどうか見る */
...
}
}
}
これは、繰り返しを表す * を使うと、
mexpr : term ( '*' term | '/' term )*;
あるいは、
mexpr : term mexpr1*;
mexpr1 : '*' term
| '/' term;
という規則で書ける。
全体のプログラムは、 s-calc.c のようになる。
実行の様子
この方法での実行では、変数dが特殊な役割を果たしている。この変数は、再帰呼び出しの途中での中間結果を保持していることになる。例えば、a=2として、(2+1030/a)-2 を考えて見よう。再帰呼び出しの数だけ、dが存在する。
| d | d | d | d | d | d | d | d | d | ||
| expr() | ? | |||||||||
| | aexpr() | ? | ? | ||||||||
| | | mexpr() | ? | ? | ? | |||||||
| ( | | | | term() | ? | ? | ? | ? | |||||
| | | | | expr() | ? | ? | ? | ? | ? | |||||
| | | | | | aexpr() | ? | ? | ? | ? | ? | ? | ||||
| | | | | | | mexpr() | ? | ? | ? | ? | ? | ? | ? | |||
| 2 | | | | | | | | term() | ? | ? | ? | ? | ? | ? | ? | 2 | |
| | | | | | | | | ? | ? | ? | ? | ? | ? | 2 | |||
| + | | | | | | | aexpr() | ? | ? | ? | ? | ? | 2 | ? | ||
| | | | | | | | mexpr() | ? | ? | ? | ? | ? | 2 | ? | ? | ||
| 1030 | | | | | | | | | term() | ? | ? | ? | ? | ? | 2 | ? | ? | 1030 |
| | | | | | | | | | | ? | ? | ? | ? | ? | 2 | ? | 1030 | ||
| / | | | | | | | | | mexpr() | ? | ? | ? | ? | ? | 2 | 1030 | ? | |
| a | | | | | | | | | | term() | ? | ? | ? | ? | ? | 2 | 1030 | 2 | |
| | | | | | | | | | | ? | ? | ? | ? | ? | 2 | 515 | |||
| | | | | | | | | | ? | ? | ? | ? | ? | 517 | ||||
| | | | | | | | | ? | ? | ? | ? | 517 | |||||
| | | | | | | | ? | ? | ? | 517 | ||||||
| | | | | | | ? | ? | 517 | |||||||
| | | | | | ? | 517 | ||||||||
| )- | | | aexpr() | ? | 517 | ? | ||||||
| | | | mexpr() | ? | 517 | ? | ? | ||||||
| 2 | | | | | term() | ? | 517 | ? | ? | 2 | ||||
| | | | | | ? | 517 | ? | 2 | ||||||
| | | | | ? | 517 | 2 | |||||||
| | | | ? | 517 | ||||||||
| | | 515 |
縦棒は手続きの寿命を表す。?は、まだ値が決まっていないdである。手続きが呼び出されるとdが一つ増えて、? が延びる。手続きが終わると、dの値が決まり、dの列が一つ短くなる。
? を省略すれば、木をたどりながら計算をする時に「とっておく必要のある値」がなにかがはっきりわかる。これは実際 stack をとっておく場所に使っている。Recursive call(再帰呼び出し)自身がstackを使って実現されているので、これはある意味では自明なことである。
| ( | ||||
| 2 | 2 | |||
| + | 2 | |||
| 1030 | 2 | 1030 | ||
| / | 2 | 1030 | ||
| a | 2 | 1030 | 2 | =a |
| 2 | 515 | =1030/2 | ||
| )- | 517 | =515+2 | ||
| 2 | 517 | 2 | ||
| 515 | =517-2 |
これがinterpreterの行っていることの本質である。
これを手順で示すと、
| ( | |||||
| 2 | 2をしまう | 2 | |||
| + | 2 | ||||
| 1030 | 1030をしまう | 2 | 1030 | ||
| / | 2 | 1030 | |||
| a | aをしまう | 2 | 1030 | 2 | =a |
| 1030/2を計算 | 2 | 515 | =1030/2 | ||
| )- | 515+2を計算 | 517 | =515+2 | ||
| 2 | 2をしまう | 517 | 2 | ||
| 517-2を計算 | 515 | =517-2 |
となる。計算する所では、stackの先頭と次の値を計算していることの注意しよう。ここまで分解すると、そのままmachine code(機械語)に落とせそうである。interpreterは、これを直接に実行してしまうが、その代わりに「こうしろ」という命令を出力すれば、compiler を作れることになる。
実際、 i386の命令 を使えば、
##### (2+1030/a)-2
## (
movl $2,%eax 2 をload
pushl %eax それをstackにしまう
## 2+
movl $1030,%eax 1030をload
pushl %eax それをstackにしまう
## 1030/
movl _variable+0,%eax 変数aを%eaxにload
movl %eax,%ebx 割算のために%ebxに移す
popl %eax 披除数をload
cltd 割算フラグのセット
idiv %ebx %eax / %ebx = %eax .. %edx
popl %ebx +2 に 2 をstackから復帰
addl %ebx,%eax %eax に足す
pushl %eax それを stack にしまう
## a)-2
movl $2,%eax 2 を load
popl %ebx さっきしまった値をとってくる
subl %ebx,%eax 引き算する
negl %eax 方向が逆なので符号を変える
call _print
となる。
スタックを使ったコード生成は、Java のbyte code でも行われている。Java の aload は、値を stack に積む命令である。
この方法で生成されたコードは、元の式の木構造に直接対応している。(push/pop が木のノードに対応する)
コード生成
実行する代わりに、「なにを実行するのか」を出力すれば、Interpreter は Compiler になる。今の簡単なInterpreterのためには以下の指示ができれば良い。- 数字Nを、手もと(Accumulator or Register)に持ってくる
- 変数Vを、registerに持ってくる
- registerの値をstackにしまう。
- スタックの上の値とregisterの値とで計算をおこなう。
- registerの値を変数に書き出す。
emit_value(d) printf("\tmovl $%d,%%eax\n",d);
emit_load(d) printf("\tmovl _variable+%d,%%eax\n",d*4);
emit_push(d) printf("\tpushl %%eax\n");
emit_calc(+) printf("\tpopl %%ebx\n"); printf("\taddl %%ebx,%%eax\n");
emit_store(assign) printf("\tmovl %%eax,_variable+%d\n",assign*4);
これを計算する代わりにInterpreterに埋め込む。この場合、返す値は必要なくなる。ここで計算する必要はないのだから。例えば、
void
aexpr()
{
emit_comment();
mexpr();
while(last_token!=EOF) {
switch(last_token) {
case '-':
emit_push();
mexpr();
emit_calc(O_SUB);
break;
case '+':
emit_push();
mexpr();
emit_calc(O_ADD);
break;
default:
return;
}
}
return;
}
となる。ここで O_SUB, O_ADD は適当な定数であり、emit_calc は、その定数に対応する計算のためのコードを生成する。
より詳しく書くと、全体のプログラムは、 s-compile.c s-code-intel.c のようになる。(これらは、/usr/open/lecture/kono/compiler/examples の下にある。他のCPU用のコード生成も書いてみたので参考にして欲しい。)
これは、構文木を下から上、右から左に沿って、何をすればいいかを書いていくことに相当する。
問題4.1
以下の式を手で木に変換して見よ。さらに、これをスタックを使って計算するintel64の命令に落として見よ。examples のコンパイラを使った結果と比較してみよ。また、gdb で実際にどのような動作をするかを調べてみよ。- 3-(4-2)
- 0+(1+(3-2))-(0+(1+(2-3)))
レジスタを使うコードの生成
今までの簡単なコンパイラでは、Register-Memory Architecture を使い、Register 1つと、Stackの先頭の演算に式をコンパイルしていた。ここでは、さらに、Load-Store Architecture を想定して、Register 上のでの演算にコンパイルして見よう。最近ではRegisterの数は16/32が多く、その中で自由に使えるものは10-20程度ある。通常の式であれば、スタックの深さは10以下であり、すべてRegister 上で計算できる。この部分を記述するのは簡単である。もっと難しいのは、複数の式でRegisterを共有する場合であり、この時には、共有する変数は非常に大量になる。これに対して適切なRegister割当をおこなうのがコンパイラの最適化として重要である。この割当の善し悪しは、関数呼出時の手間やCache(キャッシュ)の占有度に影響し、最終的にプログラム全体のPerformanceに影響する。
さて、Registerを使った式の計算は、スタックに変数を取っておく代わりにRegisterに取っておくだけである。したがって、コンパイラを変更しないで、コード生成系のみを変更するようにしようRegister 割当をおこなう s-code-sparc.c を見てみよう。
emit_push() でスタックにaccumlatorの値をsaveする代わりに、新しくaccumlator として使う Register を割り当てれば良い。このために、get_register() という手続きを考える。
#define MAX_MAX 20
static int regs[MAX_MAX]; /* 使われているレジスタを示すフラグ */
static int reg_stack[MAX_MAX]; /* 実際のレジスタの領域 */
const int MAX_REGISTER=10;
static char *reg_name[] = {"%rax","%rbx","%rcx","%rdx","%rsi", "%rdi",
"%r8", "%r9", "%r10", "%r12", "%r13", "%r14", "%r15",
"%rip", "%rbp", "%rsp" };
char * regster(int i) {
return reg_name[i];
}
static int get_register()
{ /* 使われていないレジスタを調べる */
int i;
for(i=0;i<MAX_REGISTER;i++) {
if (! regs[i]) { /* 使われていないなら */
regs[i]=1; /* そのレジスタを使うことを宣言し */
return i; /* その場所を表す番号を返す */
}
}
return -1; /* 空いている場所がないなら、それを表す -1 を返す */
}
regs[]という配列に、そのRegisterが使われているかどうかを示すflagをいれておく。get_register()では、最初のflagが空いているRegisterの番号を返す。もちろん、番号とassemblerの中でのRegister名との対応を示すものが必要なので、それは、reigster_name[]という配列を作っておく。このうちいくつかは、最初から使用不可(システムやarchitectureが使用している、例えば、SP, RTOC など)である。
どのRegisterをsaveに使ったかはコンパイラが自分で覚えてなくてはいけない。これにはスタックを使う。これは、ちょうど実行時のスタックをコンパイル時に部分計算していると考えることもできる。先に計算できる部分なわけである。accumlatorを表す Registerの番号を current_register としよう。
void emit_push() {
int new_reg;
new_reg = get_register();
if(new_reg<0) { /* もうレジスタがない */
if (reg_sp==MAX_MAX-1) {
printf("Compilation error: too complex expression\n");
} else {
reg_stack[reg_sp++] = -1;
printf("\tpushq %s\n",crn);
}
} else {
reg_stack[reg_sp++] = creg; /* push するかわりにレジスタを使う */
creg = new_reg;
crn = reg_name[creg];
}
}
char * emit_pop() {
if (pop_register()==-1) {
printf("\tpopq %s\n",drn);
xrn = drn;
xreg = dreg;
} else {
xrn = lrn;
xreg = lreg;
}
return xrn;
}
ここで、lrn は last regster name, crn は current register name につもりである。どうせ、すぐ使うのだから、ここで代入しておこう。emit_load, emit_store,
emit_value は、current_register に値をいれるだけなので、以下のように簡単に書くことができる。
void emit_value(int d) ;
{
printf("\tmovq $%d,%s\n",d,crn);
}
void emit_store(int assign) {
int tmp = get_register();
printf("\tmovq _v@GOTPCREL(%%rip), %s\n",reg_name[tmp] );
printf("\tmovq %s, %d(%s)\n" ,crn, assign*8, reg_name[tmp]);
free_register(tmp);
}
void emit_load(int d)
{
int tmp = get_register();
printf("\tmovq _v@GOTPCREL(%%rip), %s\n",reg_name[tmp]);
printf("\tmovq %d(%s),%s\n" ,d*8, reg_name[tmp],crn);
free_register(tmp);
}
実際の計算を行うところでは、stackを一つ下げることをおこなう必要がある。ここではRegister-Register演算をおこない、入らなくなったRegisterの regs[] に 0 を入れれば良い。これは pop_register()という手続きにしよう。
static int
pop_register()
{ /* レジスタから値を取り出す */
int i,j;
j = creg;
i = reg_stack[--reg_sp];
if(i<0) {
return i;
} else {
lreg = i;
lrn = reg_name[lreg];
regs[i]=0;
return lreg;
}
}
ここでは、スタックを使う場合のように、最後の結果が最初のRegisterになるように工夫している。
static
char *opcode[] = {
"", "subq", "addq", "imulq", "idivq", "",
"", "", "", "subq", "idivq",
};
void emit_calc(enum opcode op) {
char *orn;
orn = emit_pop();
if(op==O_DIV) {
// crn -> rax
// rdx !!!
printf("\tcltd\n");
printf("\tidivq %s\n",orn);
} else if(op==O_SUB) {
printf("\t%s %s,%s\n",opcode[op],orn,crn);
printf("\tnegq %s\n",crn);
} else {
printf("\t%s %s,%s\n",opcode[op],orn,crn);
}
}
これにより、スタック上での演算よりも確実に高速なコードを出すことができる。しかし、単純にレジスタを使うだけでは十分ではない。例えば、
0+(1+(2+(3+(4+(5+(6+(7+8)))))))-(0+(1+(2+(3+(4+(5+(6+(7+8))))))))
のような場合は、レジスタをかなり多く必要とする。である。しかし、これを
0+1+2+3+4+5+6+7+8-(0+1+2+3+4+5+6+7+8)
と書き換えるとReisterは一つしか使わないで済む。もちろん、中間木を使ってコンパイル時に定数計算をしてしまえば、もっと簡単になるが、ここでは簡単のために、それはおこなっていない。
このような書き換えは簡単だと思うかも知れないが、実際には同等な式への変換は無数にあり、もっともRegisterが少なくなるような式の変形は自明ではない。このような変形を行うためには中間木への変換が必ず必要となる。このような式の変換に付いても後で議論することにしよう。
拡張に付いて
Interpreter の拡張はやさしい。特に動いているものを手直しするのは簡単である。最近の言語では、実行時に新しい関数や、外部とのInterface を許すものもある。なるべく、全体の文法構造を変えないように拡張するのがこつであり、言語も拡張が容易なように設計するべきである。
問題4.2
s-calc.c の若干の改良を試みる。あとでコンパイラに書き換えることを前提にいくつかの機能をつけ加えて見よう。- termとして8進数や16進数 (楽勝)
- -1 や -a (楽勝)
- AND(&)やOR(|)の計算 (楽勝)
- <<,>> などの算術シフト (楽勝)
- Cの三項演算子a?b:c (コンパイルは難しい)
- 制御構造 while, for 文など (難しい)
- 配列 (宣言を別にするのが簡単だろう)
- 手続き呼び出し (入力テキストをすべて取っておく必要がある)
- 浮動小数点 (全体的な改良が必要になる。すべの数を小数点で計算するのが楽だろう)
実行結果と、変更した主要な部分を明示せよ。
問題4.3
0+(1+(2+3))-(0+(1+(2+3))) の式の計算を上のcompiler によりintel64の命令に変換した結果を記述せよ。0+1+2+3-0+1+2+3 の場合はどうなるか?
コンパイラのデバッグ
コンパイラのデバッグは、通常のデバッグよりも複雑で、何回かの段階をへる必要がある。まず、コンパイラがちゃんと動作することを調べる
次に、コンパイラの出力が、ちゃんとコンパイルできることを調べる
そして、その出力が正しく動作していることを調べる
特にコンパイラ自身をコンパイルできることを調べる
自分自身でコンパイルしたコンパイラが、もともとあるコンパイラでコンパイルしたものと同じ出力を持つことを確認する。
もし、コンパイラの動作がおかしかったから?
どこで動作がおかしくなったかを調べる
この時に、gdb を使ったアセンブラのデバッグを行う
disassm disassember
b *0x23423 そのアドレスでbreak
stepi 一命令実行
nexti 同上
p $eax レジスタ %eax を表示
cont 実行を再開
cond 3 if lineno==300 lineno という変数が300になったら停止
ignore 3 100
そして、おかしなコードを生成しているコンパイラの部分を修正する