Compiler Construction Lecture No.9
Menu Menu
Micro-C の全体構成
Micor-C の全体構成変数等の宣言 (モードに依存する文法)
文法規則だけでは解釈する情報が足りない場合がある。例えば、Micro-C では、Cの以下の宣言を一つの文法で済ましている。
- global変数/関数の宣言
- 関数の引数の宣言
- local変数の宣言
- 構造体の中の宣言
45 #define TOP 0
46 #define GDECL 1 /* global 変数 */
47 #define GSDECL 2 /* global struct */
48 #define GUDECL 3 /* global union */
49 #define ADECL 4 /* argument 変数 */
50 #define LDECL 5 /* local 変数 */
51 #define LSDECL 6 /* local struct */
52 #define LUDECL 7 /* local union */
53 #define STADECL 8 /* static */
54 #define STAT 9 /* function の最初 */
55 #define GTDECL 10 /* global typedef */
56 #define LTDECL 11 /* local typedef */
によって区別されている。getsym() では、このmodeを見ながら、どの処理を変えている。ただし、このmodeによる区別はプログラムの見通し悪くするので使い方には気を付けよう。
Symbol Table
Tokenizerでは、記号の切り出しとkeywordの切り出しをおこなう。同時に、名前の登録をおこなう必要がある。実際、Tokenizerが、普通の名前、(例えば英字で始まる英数字の列などだが)に出会ったとしよう。それは、名前(name)、つまり、予約語(reserved word)か、変数名か関数名である。Micor-C では、getsym() という関数がTokenizerである。これらは compiler 内部の表に登録されなければならない。この表を Symbol Tableという。Interpreter の場合でもSymbol Tableは必要である。Compilerが出力したコードでは、Symbol Tableは不要である。しかし、分割compile (Separate compilation)の場合は、相互のSymbol Tableを接続する必要があるので、Symbol Table そのものも出力しなくてはならない。この問題は、異なるcomputer上で分散計算を行う場合にも出て来る。
名前には様々な属性がある。例えば、ある名前はlocalであり、ある関数や、関数の一部でしか有効でない。ある名前で指し示される(実体/objectゥ)ものは、名前で呼ばれなくなった後も存在し続ける場合がある。あるいは、そのようなものを別な名前で呼びたい時もある。このような属性には以下のようなものがある。
- 名前の有効範囲 (scope)
- objectの寿命 (extent)
- objectの型 (type)
- local 名前は{}の中で有効であり、その外では使えない。object も、その外では消滅してしまうのでアクセスしてはならない。{}は入れ子(nest)することができるので、名前の有効範囲もnestする必要がある。しかし、C では実際には、nest は処理されずに、local 変数は、手続の中で一意な名前でなければならない。自動的にobjectが作られ、自動的に消滅するので、自動変数(auto)とも呼ばれる。Cではこちらの呼び方の方が正式である。local variableのobjectは通常はstack上に取られる。したがって、特に、pointer を使ってlocal 変数を手続き呼び出しから返してはならない。Cでは、local変数の初期化を行うことができる。Cにはlocalな手続き名は存在しない。
- global 名前とobjectは、プログラム全体で有効であり、存在する。C++では、この名前の有効範囲を class 単位にすることができる。分割 compile する場合は、この名前はコード中に出力する必要がある。分割 compile 後、さらに、link された完全なコードには symbol table は必要ない。しかし、debug のためにわざと情報を残すこともある。(-g flag in cc)。最近のOSでは、kernel levelで library の dynamic loadingを行う。場合もあり、この場合もlinkのための情報を残す必要がある。別なファイルのglobalを参照したい時には、externを使う。
- static objectは、プログラム全体で有効であり、存在する。しかし、名前はファイル内部でしか有効ではない。localなstaticという名前もあり、この場合は、名前の有効範囲は関数または{}の内部ということになる。
- macro マクロ(macro)名は、通常compilerが処理する前に変換されてしまう。したがって、compilerからも見えない名前である。しかし、Micor-C ではマクロも1 pathで処理するために、マクロ名も自分で管理する。この名前の有効範囲は分割compile単位である。マクロには引数があることがあるので、その処理も必要だが、Micro-C自身には、その機能はない。しかし、付加することはそれほど難しくはない。
compilerにとって問題なのは変数の有効範囲であり、大域名(global)と局所名(local)が衝突した場合には大域名を優先する必要があり、局所名が有効でなくなれば、その名前を再利用する必要がある。
名前には、その名前が指すもの(object)の型がある。一つの名前には一つの型がある言語(Cはそうだ)もあるが、一つの名前を複数の型に使うことができるもの(Perlなど)もある。前者の場合は、名前を検索することにより型が分かる。しかし、後者の場合には、型は名前とは別に指定する必要がある。後者の方がどちらかといえば優れているようである。Cには以下のような型がある。
- long, int, short, char 基本的な型。アセンブラでのword,2byte,1byteに相当する。
- unsinged/singed 符号が付くかどうか。引き算などで2の補数として扱うかどうかに相当する。Micro-Cには、signed char, unsinged char などは存在しない。
- float, double Micro-Cにはない。
- * pointer Cを特徴づける型。直接にobjectを指すのではなく、object のaddressを表す型である。単なるaddressではなく、足し算が定義されている。1を加えることにより、指し示すobjectの大きさの分だけaddressが加算される。大きさは、sizeof()という内蔵関数で取り出すことができる。sizeof(char) == 1であるけれど、sizeof(int)==sizeof(int *)であるとは保証されない、ということを覚えておこう。pointerのpointerという型もある。これを理解しているかどうかでCを理解したかどうかが決まる重要な部分である。
- array[10],array[],array[10][20] 配列。pointerを使ってアクセスされることが多い。2次元配列と、pointerの配列の違いを理解しよう。
- struct, union ユーザ定義可能な型。レコード型などと呼ばれることもある。複数の型を合わせて一つのobjectとして扱うことができる。
さらに、Cには、cast という概念があり、型を変換することができる。この時の構文はなかなか面白い。このあたりのcompileの詳細は、また後日、追求することにしよう。
Implementation of Symbol Table
Symbloc Table(記号表)の実装は、さまざまな方法があるが、hash tableと、stack を組み合わせるのが容易である。localな名前は、stack上に作られる。入れ子(nest)になったものを実現する場合には常にstackを使う。localな名前が作れる度に名前はstackにつまれる。そして、compileが、そのscope(手続き、または{}(statement))から抜けると、必要な所までstackを開放する。検索を、localな名前を格納したstack そして、大域名を格納したhash tableという順番に探すことにより、Cの変数の有効範囲を実現することができる。
名前にはreserved word(予約語)が取られることがある。例えば、if, for, continue などはCの予約語である。これらの語を字句解析のレベルで切り分ける手もあるが、ユーザの定義よりも先に表に登録してしまうという手もある。すると、reserved wordかどうかは、一種の名前の型となる。 </p>
さて、Micro-CではSymbol tableは以下のように定義されている。
168 typedef struct nametable {
169 char nm[9];
170 int sc,ty,dsp; } NMTBL;
171
172 NMTBL ntable[GSYMS+LSYMS],*nptr,*gnptr,*decl0(),*decl1(),*lsearch(),*gse
arch();
9文字しか変数名は見ないらしい。逆に言えば、iという変数に対しても9文字分のデータが取られている。実用的にはこんなものかも知れない。GSYMS,LSYMSは、global, local の記号の最大値である。定数は、このように大文字のマクロで書くのが C 流である。sc は、たぶん、symbol class の意味で、以下のどれかである。これと ty との値で型が決まる。ty には、struct, unioon を表す木構造(tree)か INT が入る。
- EMPTY
なんだか分からないもの
- RESERVE
予約語
- FUNCTION
手続名
- LVAR
local variable
- TYPE
型名
- TAG
struct, unicon のfieldの定義
- FIELD
struct, unicon のfieldの参照
- FLABEL,BLABEL
label (未定義=forward label)
- MACRO
macro で定義された名前
さて、getsym()を見てみよう。
2520 getsym()
2521 {NMTBL *nptr0,*nptr1;
2522 int i;
2523 char c;
2524 if (alpha(skipspc()))
2525 { i = hash = 0;
2526 while (alpha(ch) || digit(ch))
2527 { if (i <= 7) hash=7*(hash+(name[i++]=ch));
2528 getch();
2529 }
2530 name[i] = '\0';
2531 nptr0 = gsearch();
2532 if (nptr0->sc == RESERVE) return sym = nptr0->dsp;
ここでは、hash table という技術を使っている。名前によって決まったrandamな値により、表を引く。このようにすることにより、randamな値が重ならなければ一度だけで記号に対応する値を取りだすことができる。2527ではhashを計算するだけで、実際の検索は、gsearch(),lsearch() でおこなう。
2661 NMTBL *gsearch()
2662 {NMTBL *nptr,*iptr;
2663 iptr=nptr= &ntable[hash % GSYMS];
2664 while(nptr->sc!=EMPTY && neqname(nptr->nm))
2665 { if (++nptr== &ntable[GSYMS]) nptr=ntable;
2666 if (nptr==iptr) error(GSERR);
2667 }
2668 if (nptr->sc == EMPTY) copy(nptr->nm);
2669 return nptr;
2670 }
2671 NMTBL *lsearch()
2672 {NMTBL *nptr,*iptr;
2673 iptr=nptr= &ntable[hash%LSYMS+GSYMS];
2674 while(nptr->sc!=EMPTY && neqname(nptr->nm))
2675 { if (++nptr== &ntable[LSYMS+GSYMS]) nptr= &ntable[GSYMS];
2676 if (nptr==iptr) error(LSERR);
2677 }
2678 if (nptr->sc == EMPTY) copy(nptr->nm);
2679 return nptr;
2680 }
このsearchは、もし表になかった場合には登録も行う。これは標準的な実装である。lsearch()とgsearch()の差はどこにあるか考えてみよう。
2532 if (nptr0->sc == RESERVE) return sym = nptr0->dsp;
2533 if (nptr0->sc == MACRO && !mflag)
2534 { mflag++;
2535 chsave = ch;
2536 chptrsave = chptr;
2537 chptr = (char *)nptr0->dsp;
2538 getch();
2539 return getsym();
2540 }
2541 sym = IDENT;
2542 gnptr=nptr=nptr0;
2543 if (mode==GDECL || mode==GSDECL || mode==GUDECL ||
2544 mode==GTDECL || mode==TOP)
2545 return sym;
2546 nptr1=lsearch();
2547 if (mode==STAT)
2548 if (nptr1->sc == EMPTY) return sym;
2549 else { nptr=nptr1; return sym;}
2550 nptr=nptr1;
2551 return sym;
2552 }
検索が修了すると、その後で予約語とマクロの処理を行う。どちらでもなければglobalかlocalかどちらかである。この後、その記号のscとtyが決まることになる。これらは、構文解析の途中で決定するので、そこで代入される。mode
により、記号の扱いが変わることに注意しよう。
左辺値と右辺値 left value and right value
ポインタや構造体が出て来ると、代入文も複雑になる。代入文は以下のような構造をしている。
left value = right value
s-compile.c では、left value は単純(英字一文字!)だったが、今度は配列の引数や構造体へのポインタなどを計算しなくては代入ができない。
これらは、最終的にはload/storeの機械語に落ちるはずである。つまり、どのアドレス(address)から、どれくらい(size)を loadして、どれくらいをstoreするのかを決めれば良い。
Micro-C では、i386の汎用Registerを使ってaddressを計算する。実際には、%ebxなどの3種類のポインタを使い分けている。
- %ebx -- 汎用のポインタ
- %ebp -- 局所変数を指し示すポインタ
- address -- 大域変数
- movl (%ebx),%eax ------ 任意のアドレスからのload
- movl %eax,count -------- count という大域変数へのstore
- movl -16(%ebp),%eax ------- 4番目の局所変数からのload
left valueもright valueもアドレスを計算するところまでは同じである。そこで、Micro-C では expr はアドレスまで中間木を生成し、必要な時にrvalue()という手続きにより値をloadする中間木を生成している。もちろん、定数などはアドレスを計算しなくても直接にloadされているので、rvalue() は何もしない。
ravlue() は短いが、それを理解するためには、Micro-C の中間木を理解しなくてはならない。
Micro-C の中間木
Micro-C での木を扱う手続きには奇妙な名前をした関数(function)が使われている。
2836 car(e)
2837 int e;
2838 { return heap[e];
2839 }
2840 cadr(e)
2841 int e;
2842 { return heap[e+1];
2843 }
2844 caddr(e)
2845 int e;
2846 { return heap[e+2];
2847 }
2848 cadddr(e)
2849 int e;
2850 { return heap[e+3];
2851 }
2852 list2(e1,e2)
2853 int e1,e2;
2854 {int e;
2855 e=getfree(2);
2856 heap[e]=e1;
2857 heap[e+1]=e2;
2858 return e;
2859 }
2860 list3(e1,e2,e3)
2861 int e1,e2,e3;
2862 {int e;
2863 e=getfree(3);
2864 heap[e]=e1;
2865 heap[e+1]=e2;
2866 heap[e+2]=e3;
2867 return e;
2868 }
2869 list4(e1,e2,e3,e4)
2870 int e1,e2,e3,e4;
2871 {int e;
2872 e=getfree(4);
2873 heap[e]=e1;
2874 heap[e+1]=e2;
2875 heap[e+2]=e3;
2876 heap[e+3]=e4;
2877 return e;
2878 }
2879 getfree(n)
2880 int n;
2881 {int e;
2882 switch (mode)
2883 {case GDECL: case GSDECL: case GUDECL: case GTDECL:
2884 e=gfree;
2885 gfree+=n;
2886 break;
2887 default:
2888 lfree-=n;
2889 e=lfree;
2890 }
2891 if(lfree<gfree) error(HPERR);
2892 return e;
2893 }
2894 rplacad(e,n)
2895 int e,n;
2896 { heap[e+1]=n;
2897 return e;
2898 }
これらの関数名は、LISPというLIST処理専門に設計されたプログラミング言語から来ている。しかし、Micro-CでのLISTは、やや簡略化された形で実装されている。本来は、list2()などは、配列ではなくLISTを返すべきだ。これは Micro-Cでは8bit CPUつまり、64kbyteのメモリ空間を想定しているので、LIST(2進木)を使うことによりメモリをより多く消費することを嫌ったのだと思われる。
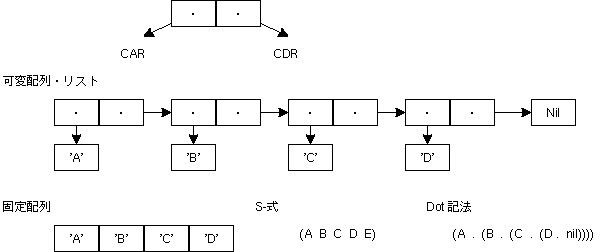
この(簡略化された)LIST(専門的にはcdr codingというのだが、そんなことはどうでもいいことなのだが...)の、最初の要素をcar()、次の要素をcadr()、次の次の要素をcaddr() という。(最近のLISPでは、first(), second(), third() を使うのが普通なようだ) 木には葉(leaf)と幹(node)があるのだが、car()の値によって、それらを区別している。cadr()とかの内容はcar()によって異なる。これはかなり複雑だが、実際には、car()の値によって処理を変えれば良いだけだ。
どのような中間木のノードがあるかは、list2 などをgrepしてみれば簡単にわかる。(が、かなりあるので、ここでは省略する) Micro-C では、変数の型も木で表している。したがって、式を表す木と型を表す木の二つの木を扱うことになる。型は常にtype という変数に入っている。この二種類の木は、違う構造をしているので気をつけて扱わなくてはならない。
ここで出て来るINDIRECTとADDRESSが、Cの配列や構造体、そして、ポインタに対応している。これらは、どういう構文で生成されるのだろうか?
indirect and reference
Cでは、以下のポインタ演算が可能である。- &p ---- p のアドレス ADDRESS
- *p ----- pのアドレスの指し示す先 INDIRECT
1183 case MUL:
1184 getsym();
1185 e=rvalue(expr13());
1186 return(indop(e));
1187 case BAND:
1188 getsym();
1189 switch(car(e=expr13()))
1190 {case INDIRECT:
1191 e=cadr(e);
1192 break;
1193 case GVAR:
1194 case LVAR:
1195 e=list2(ADDRESS,e);
1196 break;
1197 case FNAME:
1198 return e;
1199 default:error(LVERR);
1200 }
1201 type=list2(POINTER,type);
1202 return e;
indop()では以下のように中間木を生成する。
1368 indop(e)
1369 int e;
1370 { if(type!=INT&&type!=UNSIGNED)
1371 if(car(type)==POINTER) type=cadr(type);
1372 else error(TYERR);
1373 else type= CHAR;
1374 if(car(e)==ADDRESS) return(cadr(e));
1375 return(list2(INDIRECT,e));
1376 }
array and struct
array と struct は、アドレスを考えれば、統一的に扱うことができる。例えば、a[4]というのは、a+4 というアドレスだし、a->type というのは、a の指し示す構造体ののアドレスにtypeというoffsetを足したアドレスである。実際に、expr16()では、indop()を使ってarrayとstructの中間木を作っている。Cから見た時には、すべてはアドレスと、その指し示す先の大きさでしかない。大きさは型から決まる。
1312 expr16(e1)
1313 int e1;
1314 {int e2,t;
1315 while(1)
1316 if(sym==LBRA)
1317 { e1=rvalue(e1);
1318 t=type;
1319 getsym();
1320 e2=rvalue(expr0());
1321 checksym(RBRA);
1322 e1=binop(ADD,e1,e2,t,type);
1323 e1=indop(e1);
1324 }
1325 else if(sym==LPAR) e1=expr15(e1);
1326 else if(sym==PERIOD) e1=strop(e1);
1327 else if(sym==ARROW) e1=strop(indop(rvalue(e1)));
1328 else break;
1329 if(car(e1)==FNAME) type=list2(POINTER,type);
1330 return e1;
1331 }
.....
1377 strop(e)
1378 { getsym();
1379 if (sym!=IDENT||nptr->sc!=FIELD) error(TYERR);
1380 if (integral(type)||car(type)!=STRUCT && car(type)!=UNION)
1381 e=rvalue(e);
1382 type = nptr->ty;
1383 switch(car(e))
1384 {case GVAR:
1385 case LVAR:
1386 e=list2(car(e),cadr(e) + nptr->dsp);
1387 break;
1388 case INDIRECT:
1389 if(!nptr->dsp) break;
1390 e=list2(INDIRECT,list3(ADD,cadr(e),list2(CONST,nptr->dsp
)));
1391 break; 1392 default: 1393 e=list2(INDIRECT,list3(ADD,e,list2(CONST,nptr->dsp))); 1394 } 1395 getsym(); 1396 return e; 1397 }
ポインタに関するコード生成
これらの中間木はgexprによってコード生成される。
1663 gexpr(e1)
1664 int e1;
1665 {int e2,e3;
1666 if (chk) return;
1667 e2 = cadr(e1);
1668 switch (car(e1))
1669 {case GVAR:
1670 leaxy(e2);
1671 return;
1672 case RGVAR:
1673 lddy(e2);
1674 return;
1675 case CRGVAR:
1676 ldby(e2);
1677 sex();
1678 return;
....
1829 case ASS: case CASS:
1830 assign(e1);
1831 return;
1832 case ASSOP: case CASSOP:
1833 assop(e1);
1834 return;
GVARがleft value、RGVARがright valuewを表している。代入文は、さらに、assign()というコード生成手続きを呼び出す。
2014 assign(e1)
2015 int e1;
2016 {char *op;
2017 int e2,e3,e4,e5,l;
2018 op = (car(e1) == CASS ? "STB" : "STD");
2019 e3 = cadr(e2 = cadr(e1));
2020 e4 = caddr(e1);
2021 switch(car(e2))
2022 {case GVAR: case LVAR:
2023 gexpr(e4);
2024 index(op,e2);
2025 return;
2026 case INDIRECT:
2027 switch(car(e3))
2028 {case RGVAR: case RLVAR:
2029 gexpr(e4);
2030 indir(op,e3);
2031 return;
ここで、index()がSTBやSTDを生成していることが分かる。indir()では、LDB [,X] なdが生成されて6809のindirect addressing を有効に使用している。
binop(), assign() などは、さらに細かい処理を行っているので、このあたりを読んで見るとcompilerの構文木の生成と、コード生成の実際が良く分かるはずである。特にアドレスの足し算、引き算では、特別な扱いをしていることに注意しよう。
問題9.1 以下のCのstatementに対応するMicro-Cの中間木と生成されるi386のコードについて考察せよ。ただし、以下のint *a; という型を仮定する。
- *a = 1;
- a = &a[3];
- *a = *(a + a[3] + 2);
- a = *( &a + 3);
問題9.2 &a = (int *)3; というのは、Micro-C ではエラーになる。なぜ、エラーなのかを説明せよ。
共通部分式の抜きだし
基本ブロックの最適化では共通の式などを抜きだす。このためには、基本ブロックの中の式を一度、DAG グラフ(Directed Acyclic Graph)に直すのが良い。DAGの作り方
- 入力となる変数を一番下に置く
- 演算を行った順に、演算のノードを作る
- この時に同じ形のDAGは再利用して良い (これにより共通部分式(common expression) を取り除くことができる)
- 結果を変数に代入する時にはノードの横に変数名を書く
問題9.3
以下のプログラムのDAGを作成せよ。できれば、作成したDAGにしたがってi386 のアセンブラを作成せよ。
A: a=b+c; b=a-d; c=b+c; d=a-d;
B: a=b+c; b=b-d; c=c+d; e=b+c;
C: e=a+b; f=e-c; g=f*d; h=a+b; i=i-c; j=i+g;
ヒント。単にグラフの形だけでなく、式の意味を考えて共通部分式としても良い。
局所的最適化 Local Optimization
局所的最適化の代表的なものは peep hole optimization と呼ばれるものである。これはいったんコードを生成した後に、そのコードを狭い範囲で見て、より良いものに置き換えられるならば置き換えるというものである。共通部分式の置き換えなどはできないが、簡単で効果的であることが知られている。コード生成の時点で行ってしまっても良い。例えば、micro-C ではそうなっている。- mov r3,a(r31); mov r3,a(31) などは後者は必要がない
if(0) {...} などの決まった条件分岐を消す - 連続した分岐を一つにする
- a+0, a*1 などの計算を止める
- a*2 などを足し算で置き換える
- load and update などのPowerPC独自の機能を使う