学生実験2 : 探索アルゴリズムその1





更新情報
  • [2007-11-08] 作成中・・・．
  • [2007-11-13] 公開．
  • [2007-11-13] UML関連リンクを追加．
  • [2007-11-15] UML関連リンクを追加．課題提出方法を修正．
  • [2007-11-16] Level2に関するxの定義域制約を修正．
  • [2007-11-18] レポート提出期限を「期限実施日＋10日まで」，口頭試問期限を「レポート提出後＋4日まで」としました．
  • [2007-11-22] レポート提出先のディレクトリ名を変更しました．クラスによって異なりますので注意してください．



進め方

内容と目標
  • 復習を兼ねて，実験1で学んだ技術（スクリプトプログラミング）の応用．
  • 人工知能関連科目（人工知能，ニューラルネット，知能ロボット，実験3/4（進化計算，知能ロボット））へのイントロダクション．
  • グループ討論，計算機実験を通して探索や最適化のイメージを掴むとともに，計算機実験を効率良く実施するために何を考慮すべきかを理解し，それを実現するための基礎技術を身につける．
  • 関連技術に関するサーベイ（調査）と応用する技術の獲得．
  • 目的達成のための手段を提案・調査・検討し，複数代替案の中から適切なアプローチを選択する考察能力を身につける．
実験の進め方
  • グループ作業．

    各課題についてグループ間で議論し，プログラミング，考察，文書作成等を共同作業で行う事．あるテーマについて議論し，意見をまとめ，行動し，その結果を考察・報告する一連の作業（See also PDCAサイクル）を実施する事も本実験の課題である．作業分担についてはこちらからは指定しないが，各自担当した箇所が分かるように明示する事．

  • 各レベル毎に，「解説→グループ討論（実装，計算機実験，考察）→全体討論（報告会）」を行う．
評価基準

報告会では，主にプレゼンや質疑応答により「コミュニケーション能力と国際性，論理性」を中心に評価する．

レポートでは，指定した課題をこなしている（提出している）事を前提に基準点を設け，以下の項目に沿って加点・減点を行う．参考までに各レベルの点数を掲載することで難易度（求めるレポートの質・量）を示しているが，必須のレベル（オプションと書いてある箇所以外全て）は全てこなすこと．一部の課題をやらなかった場合には，該当レベル分の点数を減じるだけではなく，ペナルティとして-10点をカウントする．

口頭試問（レポート提出時もしくは後日実施）では，レポート概説や質疑応答により「コミュニケーション能力，論理性」を中心に（なるべく個別に）評価する．

レポートの基準点は63〜68点，報告会と口頭試問の両方で10点，合計73〜78点程度であり，課題を無難にこなすだけでは優（80点〜）にはならない．積極的にオプション課題や関連技術について取り組み，加点を勝ち取るように．

加点
  • 独自に行った関連課題に関する報告（積極性）．
  • 実験中に示した手法ではなく，自力で探し出した異なる手法で問題を解決した場合（積極性・実践性・創造性）．

    original/prevenience/traditional を問わないが，実験が主目的であるため可能な限り動かすよう努力すること．サンプルソースやツール等が動かない場合にはその原因究明についてレポートする事も一つの報告方法である．

  • 手法の利点・欠点や限界等に関して自主的にトライした結果・考察が示されている場合（積極性・専門性）．
  • レポートの見せ方に関する工夫や，グループ作業に伴う支援ツール等の利活用（コミュニケーション能力）．
  • その他，本テーマに関連する実験的側面上「積極性・実践性・創造性・コミュニケーション能力」等の観点から評価できるもの．
減点
  • 先行研究や事例，レポート，web等を参照しているにも関わらず，それらを参考文献として参照していない場合（一般倫理）．
  • 論理的矛盾が見られる場合（論理性）．
  • 結果を示さずに考察のみを記載してたり，結果に対する考察に整合性が見られない場合（コミュニケーション能力）．
  • タイプミスや可読性の欠如（特に，図が読めないレポート多し！），数式等記号の印字ミス，提出期限の遅れ等，多方面に関して大きな誤りではない場合．
  • 提出遅延に関しては減点ではなく「受け付けません」．

課題と提出方法
  • オプションを除く全ての Level にトライし，レポートとしてまとめよ．その際（もしくは後日），レポートに関する簡単な口頭試問を行うので，口頭試問の期日に関して別紙/メールにて予約をする事．
  • 1グループ1レポート提出．
  • メンバ（氏名・学籍番号）と担当内容を記載すること．
  • 提出物は以下の2つです．それらを「groupX」というフォルダに準備し，規定の場所に提出（アップロード）してください．印刷する必要はありません．
    • 提出物1: レポートファイル

      補足：LaTeXで作成し，PDF化したもの．

    • 提出物2: プログラム等の関連ファイル一式を圧縮したもの

      補足：tar.gz で圧縮する事．

  • 提出（アップロード）の方法

    1. 上記2つを「naha:~tnal/2007-search1/」に rsync で提出してください．保存する際のディレクトリ名は「groupX」のようにグループ名を使用する事．
    例えば，iBook 上の ~/group1/ に提出物を保存しているならば，以下のように rsync する事で提出できます． rsync 自体の説明は例えばここを参照してください． 

    #実施日によってアップロード先が異なります！
#月曜日のクラスは「2007-search1-mon」へ．
prompt> rsync -auvze ssh ~/group1/ \
e0657xx@naha:/net/home/teacher/tnal/2007-search1-mon/group1/

#金曜日のクラスは「2007-search1-fri」へ．
prompt> rsync -auvze ssh ~/group1/ \
e0657xx@naha:/net/home/teacher/tnal/2007-search1-fri/group1/

    2. 提出後，提出報告をメールにて連絡ください． 確認次第リプライを返します．

  • プログラムのソースをレポート中に含める場合には，必要十分に留めること．不必要に全ソースを掲載するのは×．
  • レポート提出期限：実験日の10日後までに 705 室へ（11/16のクラスの期限は11/26日，11/19のクラスは11/29）．

    提出期限を過ぎたら，原則的に，受け取りません． 期限内に仕上げる事も重要なタスクです． ただし，一般社会でも通用する理由で遅れてしまう場合にはこの限りではありませんので，なるべく早く相談してください．

  • 口頭試問期限：レポート提出時が望ましいが，別日程にて行う場合には，遅くともレポート提出から4日程度を目安に予約する事．
  • 採点後，優秀なレポートを期間限定で公表します．




1. 探索とは？

前提

（探索が何なのかを考える前に・・・） コンピュータを利用して効率良く問題解決したい． 特に，ここでは AI で対象とする問題を解決するための一般的枠組みを学ぶ．

  • AI で対象とする問題：ゲーム理論，音声/画像認識，ロボティクス，マイニング，予測，同定，，，
  • 参考：人工知能研究（What's AI @ 人工知能学会）

Level 1.1 : コンピュータと人間の違いを述べよ (4点)
コンピュータが人間より得意とするモノは何だろうか？逆に，人間より不得手のモノは？
注記：レポートでは，各々2つ以上を列挙して説明する事．
Level 1.2 : 具体事例を挙げ，「探索」という観点から考察せよ (9+5点)

システムが実世界で作業をする問題（具体事例）を1つ挙げ，その問題を解決するに当たって必要となる機能・技術等について論じよ．項目毎に，人間とコンピュータとの対比という点でまとめること．もしくは，該当システムに「＊＊機能が追加されるとより便利になる．この機能を実現するには・・・」といった提案形式でも構わない．

既存システムの調査報告のみとなる場合には9点，新規提案の場合には更に+5点を基準点とする．

具体事例の例

ここでいう具体事例とは，ロボリアのように単体で完結しているシステムでも， Honda スマートマーキングアシストシステムや レスキューロボット のように，人間と共同作業を含めるものでも構わない． なお，必ずしもロボットのような体を有するシステムである必要はなく， Googleの検索エンジン・広告， Amazonのお勧め商品・Amazonおまかせリンク（TM）， はてなやYouTubeの検索（タグ機能） のように，電子媒体を情報源とするものでも構わない．

レポートには以下の項目を含めること．
  • システム概要図（全体）と，探索対象となる問題との関連図．ただし，全体図そのものが探索対象になっている場合には，図は一つで良い．

    図はフローチャートや，UML（ユースケース図 1, 2や，アクティビティ図1, 2等）を参考にすると良いでしょう．

  • 探索対象に対して・・・
    • 入力・内部モデル・出力の説明．
    • 問題空間の定義や説明，この問題ならではの特徴など．
    • 探索方法の説明（提案）．
  • 参考にした文献/Webサイト等があれば，必ず示す（参考文献として列挙し，参照する）こと．
Level 1.x: 問題解決(オプション)

人間と全く同じことができるのであればただのマンパワーとして考えれば良いが，コンピュータはそうではない． では，コンピュータに取って都合の良い解決方法があるのだろうか？

そもそも人間の行っている問題解決とは？ どうすればそれを工学的に実現できるか？




2. 連続関数の最適化

コンピュータで解決するには？

探索：人間のように知的に処理 <-> 全ての解を調べ尽くす

どれだけ計算資源を割り当てることができるのか，どれだけ時間資源を割くことができるのかといったコストの観点を捨て去ることはできないが，理想的には，無駄無く適切な解を求めたい．
→では，どうやって求めるのがベストな方法なのか？

Level 2 : 連続関数における探索手法を検討し，その効率を示せ．

Level 2.1 〜 2.3 に示した関数について，最急降下法により最小値を求めるプログラムを作成し，計算機実験により評価し，結果を示した上で考察せよ．

なお，最適解を求める（発見する）にあたり，出発点となる解はランダムに選ばれるものとする．

実装時のヒント

  • 微分値を利用する際，目的関数 f(x) を微分した関数 f'(x) はプログラマが設定して良い．（任意の関数 f(x) を微分出来るように実装する必要は無い）
  • 微分値が正の値の場合，最適解（最小値）は相対的にどの位置にあるか？同様に，負の値を取る場合にはどの位置にあるかを考えて実装せよ．言い換えると，「現在地 xi の微分値を求め，その値に応じて x 軸のどの方向へ探索するかを決定する必要がある．
  • 微分値を基に x を移動させる幅を決定する際，「xnext = x -α*f'(x)」とせよ．学習係数αは 0 より大きい実数とし，この値を変更する事でどのように探索が行われるかを観察せよ．
  • x は「-10 <= x <= 10」とする．
  • サンプルソース：search1-sample.tar.gz

    ランダムな初期位置の決定，指定した回数分探索を行う，定義域内を外れたら終了，の3点は実装済．詳細はソース内の 0README_ja.txt や，上記の「実装時のヒント」を参照．

    f(x), f'(x) 及び x の移動方法を実装し，実験せよ．

注記：レポートには以下の点を含めて考察する事．

  • 探索の手続き，フローチャート．
  • プログラムソース（スクリプトを含む）．

    ただし，紙に印刷する必要は無く，レポート内には最小限のみを記載した上で，ソース全体はメールに添付の上提出する事．

  • 実行結果．

    無駄に全てを示す必要はなく，第三者が読んでも理解できる程度に，必要十分に示す事．

  • 考察．

    特に学習係数αと微分値が探索に及ぼす影響について考える事．

    必要に応じて適切な図表を作成し，理解しやすい考察となるようにする事．

    効率の指標には計算量，メモリ使用量，実行時間等様々な物差しがあるが，どの指標を用いても良い．例えば，探索点（解）の数が1万個あるとし，その内何割程度の解空間を調べる事で最適解を発見できる，というような考察でもOK．

Level 2.1 : y = x　　　(6点)
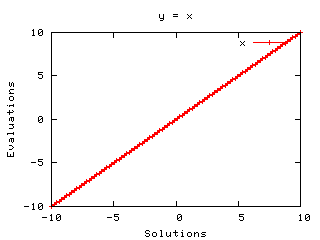
Level 2.2 : y = x2　　　(8点)
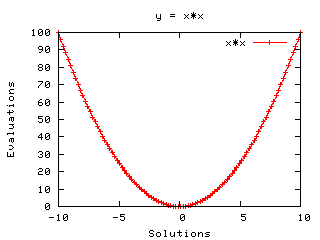
Level 2.3 : y = -x*sin(x)　　　(10点)
  • ランダムな解からスタートするため，Level 2.3 のような多峰の関数においては必ずしも最適解を発見できるとは限らない．この場合には「試行 10 回中 5回最適解を発見できた」等として，どのぐらいの確率で成功するのかを示した上で，これを改善する策について言及すること．
  • Level 2.3 では同じ最適値の解が2つあるが，このような場合どのようにすれば複数最適解を獲得出来るか，検討せよ．（オプション：実装し，結果も示すと加点）
Level 2.x: オプション
  • 結果の集計・解析ツール（言語は問わない）の作成と利活用．ソースにはコメントを付けること．
  • 最急降下法以外の手法を実装する場合には，手法名・概要を説明した上で結果・考察を示す事．オリジナルの手法ならば詳細に説明する事．



3. 不連蔵関数の最適化

Level 3 : 不連続関数における探索手法を検討し，その効率を示せ．(13x2点)

Level 3.1 〜 3.3 に示した関数はステップ関数（不連続関数）であり，微分を活用した解法は適用できない． 解空間（x軸）全てを調べる事なく，一部を調べる事で（順）最適解を求めるにはどうすれば良いか，検討せよ．

コメント
  • 実装は必須ではないが，加点対象とする．
  • 一般的に，組み合わせ最適化問題は問題空間が広すぎるため，「必ず最適解を発見する」という保証は出来ない．今回は，何らかの点で全探索よりも性能が良い事を示せる手法であればOKとする．
  • Level 3.x 毎に特化した手法を検討する必要は無い．一般的に微分が利用出来ない問題（組み合わせ最適化問題）を解く為の汎用的なアプローチを検討せよ．もしくは，特定の問題に絞ったアプローチについて検討しても良いが，その際には Level 3.2 と 3.3 の両方について検討すること．なお，問題は「組み合わせ最適化問題」に分類されるものであれば何でも良いとする．
  • Level 3.2, 3.3 は要素数の増加に伴い問題空間が指数関数的に増加する．このような問題を組み合わせ最適化問題と呼ぶ．組み合わせ最適化問題の場合には，問題空間があまりにも広大すぎるために「可能な限り無駄な探索を省く事で探索領域を狭め，効率良く良質な解を探し出す」事を目指す必要がある．
注記：レポートには以下の点を含めて考察する事．
  • 問題空間の特徴について
    • 解を構成する要素の増加に伴う問題空間サイズの増加具合を計算量及び図として示す事．
    • 要素数/問題空間サイズと全探索時の実行時間や使用メモリサイズ等の関係．

      適当な性能を持った計算機を明記し，それを利用した場合の時間として構わない．ただし，あまりにも性能が低すぎる計算機ではダメ．実際に計算させようとした時の目安が分かる指標を最低でも1つは示す事．

  • 探索の手続き，フローチャート．
  • 提案手法の利点・欠点．
Level 3.1 : y = x*sin(x) with steps
  • 解 x は整数とする．
  • x が 0...10 の時は問題空間サイズは10である．0...100の時は？
Level 3.2 : ナップサック問題
複数の品物(それぞれの品物は,重さと値段が事なる)が与えられた時,重さがナップサックに入る最大重量以内でなるべく合計の値段が最大になるような品物の組み合わせを求めよ.

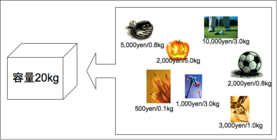
  • 品物の数が3個の時，解 x は 001(1つ目をナップサックに入れる），011(1つ目と2つ目をナップサックに入れる）という表現で表すことができる．
  • 品物の数が3個の時の問題空間サイズは？4個の時は？N個の時は？
Level 3.3 : 巡回セールスマン問題
ある2次元空間上のマップにおいて複数の都市が与えられた時，全ての都市を巡回するのに要するコスト（巡回経路長）を最小化せよ．

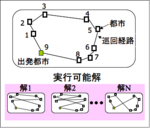
  • 都市数が3の時，解 x は123（都市1→都市2→都市3），213（都市2→都市1→都市3）という表現で表す事ができる．
  • 都市数が3の時の問題空間サイズは？4都市の時は？N都市の時は？
Level X: どのような組み合わせ最適化問題，または最適化手法があるか？
オプション課題なので，自由に考えてもらって構いません． 先行研究を調べた場合には参考文献（Webの場合はURL）を挙げる事．



参考文献・サイト