学生実験2 : 探索アルゴリズムその1
- 更新情報
- 進め方
- コンテンツ
- 1. 探索とは?: Level 1.x (5+7点)
- 2. 最急降下法による最適化: Level 2.x (7+9+11点)
- 3. 最急降下法が苦手とする状況: Level 3.x (9+9点)
- 4. モデル推定時における目的関数の設計: Level 4.x (10点)
- 5. レポート骨組み
- 6. FAQ
- 参考文献・サイト
進め方
- 内容と目標
-
- 前置き1: 復習を兼ねて、実験1で学んだ技術(スクリプトプログラミング)の応用。
- 前置き2: 人工知能関連科目(人工知能、ニューラルネット、知能ロボット、実験3/4(データマイニング班))へのイントロダクション。
- グループ討論、計算機実験を通して探索や最適化のイメージを掴む。
- 計算機実験を通して最急降下法の動作を理解し、そのメリット・デメリットを示すことができる。
- 応用事例に特化した目的関数の設計について検討し、設計理由と共に目的関数を説明することができる。
- 実験の進め方
-
- グループ作業。
各課題についてグループ間で議論し、プログラミング、考察、文書作成等を共同作業で行う事。あるテーマについて議論し、意見をまとめ、やるべき行動を設定&実行し、その結果を考察・報告する一連の作業(See also PDCAサイクル)を実施する事も本実験の課題である。作業分担についてはこちらからは指定しないが、各自担当した箇所が分かるように明示する事。
注意: 上記における「担当」や「分担」は、レポート作成上の担当であって、実験担当ではない。全員が実験を実施した上で、レポートとして整理する担当のことである。例えば、AさんがLevel 1のレポート作成を担当したとしても、BCDさんがLevel 1をやらなくて良い訳ではなく、BCDを含めた全員がLevel 1を実施する必要がある。その上で、AさんがLevel 1に関するリーダーとなって結果や考察等を整理し、レポートとして書き上げるための役割である。
- 各レベル毎に、「解説→グループ活動(討論/実装/計算機実験/考察)→全体討論(報告会)」を行う。
- グループ作業。
- 評価基準
-
報告会では、主にプレゼンや質疑応答により「コミュニケーション能力、論理性」を中心に評価する。
レポートでは、指定した課題をこなしている(提出している)事を前提に基準点を設け、以下の項目に沿って加点・減点を行う。参考までに各レベルの点数を掲載することで難易度(求めるレポートの質・量)を示しているが、必須のレベル(オプションと書いてある箇所以外全て)は全てこなすこと。一部の課題をやらなかった場合には、該当レベル分の点数を減じるだけではなく、ペナルティとして10点更に減じる。
口頭試問(レポート提出時もしくは後日実施)では、レポート概説や質疑応答により「コミュニケーション能力、論理性」を中心に(なるべく個別に)評価する。
レポートの基準点は67点、報告会と口頭試問の両方で10点、合計77点程度である。課題を無難にこなすだけではA(90点〜)にはならない。積極的にオプション課題や関連技術について取り組み、加点を勝ち取るように。
なお、探索アルゴリズム1と2のレポート2つ分の合計得点を200点満点として採点する。このため、例えば探索アルゴリズム1で130点分頑張り、探索アルゴリズム2は70点程度の時間(最低限の努力)で仕上げる、というように片方に注力するやり方であっても構わない。
加点 - 独自に行った関連課題に関する報告(積極性)。
- 実験中に示した手法ではなく、自力で探し出した異なる手法で問題を解決した場合(積極性・実践性・創造性)。
original/prevenience/traditional を問わないが、実験が主目的であるため可能な限り動かすよう努力すること。サンプルソースやツール等が動かない場合にはその原因究明についてレポートする事も一つの報告方法である。
- 手法の利点・欠点や限界等に関して自主的にトライした結果・考察が示されている場合(積極性・専門性)。
- レポートの見せ方に関する工夫や、グループ作業に伴う支援ツール等の利活用(コミュニケーション能力)。
- その他、本テーマに関連する実験的側面上「積極性・実践性・創造性・コミュニケーション能力」等の観点から評価できるもの。
減点 - 先行研究や事例、レポート、web等を参照しているにも関わらず、それらを参考文献として参照していない場合(一般倫理)。
- 論理的矛盾が見られる場合(論理性)。
- 結果を示さずに考察のみを記載してたり、結果に対する考察に整合性が見られない場合(コミュニケーション能力)。
- タイプミスや可読性の欠如(特に、図が読めないレポート多し!)、数式等記号の印字ミス、提出期限の遅れ等、多方面に関して大きな誤りではない場合。
- 提出遅延に関しては減点ではなく「原則として受け付けません」。
何らかの理由で間に合わない場合にはホウレンソウ(報告/連絡/相談)。 相応の理由がある場合には可能な範囲で事前に連絡相談してください。 事情に応じて後日でも構いませんが、なるべく早く報告してください。一般社会の常識です。
- 課題と提出方法
-
- オプションを除く全ての Level にトライし、レポートとしてまとめよ。後日、レポートに関する簡単な口頭試問を行うので、口頭試問の期日に関して別紙/メールにて予約をする事。口頭試問の実施期限は、目安として1月上旬とする。早めでも構いませんが、遅くなるのはできるだけ避けること。
- 1グループ1レポート提出&口頭試問。
- メンバ(氏名・学籍番号)と担当内容を記載すること。
- 提出物は以下の2つです。それらを「groupX」というフォルダに準備し、規定の場所に提出(アップロード)してください。印刷する必要はありません。
- 提出物1: レポートファイル
補足:LaTeXで作成し、PDF化したもの。texファイル, 図ファイル等全て含めること。
- 提出物2: 図やプログラム等の関連ファイル一式
補足:実験再現に必要なものは全て含めること。
- 提出物1: レポートファイル
- 提出(アップロード)の手順:3ステップあり。
[手順1] 上記2つを「shell:~tnal/2013-search1-xxx/(xxxは下記参照)」に rsync で提出してください。保存する際のディレクトリ名は「groupX」のようにグループ名を使用する事。
例えば、MacBook 上の ~/group1/ に提出物を保存しているならば、以下のように rsync する事で提出できます。 rsync 自体の説明は例えばここを参照してください。# 実施日によってアップロード先が異なります! # 月曜日のクラスは「2013-search1-mon」へ。 prompt> rsync -auvze ssh ~/group1/ \ e1157xx@shell:/net/home/teacher/tnal/2013-search1-mon/group1/ # 金曜日のクラスは「2013-search1-fri」へ。 prompt> rsync -auvze ssh ~/group1/ \ e1157xx@shell:/net/home/teacher/tnal/2013-search1-fri/group1/ # 注意: # ・上記の例ではコマンドが長いためバックスラッシュ「/」で区切り、 # 2行に分割して書いています。 # ・スラッシュの有無で引数の意味が大きく異なります。 # ・アップロードはグループ代表者一人が行ってください。 # パーミッションの都合上、レポート修正した後の再アップロードも # 同じ代表者じゃないとアップロードできません。
[手順2] 提出後、提出報告をメールにて連絡ください。
メールの件名は「(search1/mon/group1)」のように、テーマ名(search1)、曜日(monもしくはfri)、グループ番号」を含めるようにしてください。
[手順3] メールと提出ファイル一式を確認次第リプライを返します。
- プログラムのコードや実験結果をレポート中に含める場合には、必要十分に留めること。不必要に全ソースを掲載するのは×。
- レポート提出期限:月曜クラスは12/23(月)(公休日)、金曜クラスは12/27(金)とする。(探索アルゴリズム2も同一日です)
提出期限を過ぎたら、原則的に、受け取りません。 期限内に仕上げる事も重要なタスクです。ただし、一般社会でも通用する理由で遅れてしまう場合にはこの限りではありません。同様に、延長希望等のリクエストも適宜相談次第で受け付けますので、なるべく早く相談してください。
- 口頭試問期限:レポート提出から1週間の期間を目安に、グループメンバ全員一緒に、705室にて口頭試問を受けること。口頭試問の実施日は、空き時間目安ページ(後でURLを掲載します)を参考の上、レポート提出メールを送る際にでも希望日を連絡して下さい。
- 採点後、優秀なレポートを期間限定で公表します。
1. 探索とは?
1.1. 前提1: コンピュータと人間の違い
(探索が何なのかを考える前に・・・) コンピュータを利用して効率良く問題解決したい。そもそも効率良く問題解決する必要が無いならばコンピュータを利用する必要性はない。効率にもいろんな側面が考えられるが、ここでは特に制約を設けないものとする。
- Level 1.1 : コンピュータと人間の違いを述べよ (5点)
- コンピュータが人間より得意とするモノは何だろうか?逆に、人間より不得手のモノは?
1.2. 前提2: 「探索」における問題設定の定義
- 目的物, xopt: ユーザが望むモノ。
- 目的関数, f(x): 目的物が最適値となるように設計された関数。目的物以外のものについては、目的物との合致具合(≒近さ)に応じたスコアを返すことが多い。(例: 「最適な仕様とは何か」「そもそも何をもって最適であると判断するか」)ただし、正確な目的関数を設計する事は容易ではなく、関数が誤っているために xoptを探し出せないこともある。
- 探索, minimize or maximize: 指定された探索範囲内から目的物を探し出す事。多くの場合は前述の「目的関数 f(x)」を最大化or最小化する解 x を探し出す行為のこと。
- 制約条件, subeject to MIN_X < x < MAX_X: 目的物を探し出す際の条件。探索範囲に直接影響があるものだけではなく、時間的制約等の間接的な条件もありえる。
- 探索アルゴリズム: 探索のための手続きや方法。
- 探索システム: 指定された解空間・制約条件内において、指定のアルゴリズムを用いて目的物を探し出すシステム。必ず入力・内部モデル・出力を伴ったものとなる。
- 目的関数: f(x) = x*x
- 制約条件: subject to 1 <= x <= 3
- 探索目的: minimize f(x)
- Level 1.2 : 目的物(や目的関数)の特徴について検討してみよう (7点)
-
web検索を例に考えてみよう。勾配法について記述されているこのページは「探索」というキーワードを含まないが、内容は「探索」の一例である。この事例に限らず、webページをキーワード検索する際にキーワードマッチングだけで探し出せるページは必ずしも十分ではない。
その事を踏まえた上で、以下の事について検討せよ。
- 目的物(web検索で探し出したいページor項目)についての特徴は?
- Level 1.x: 問題解決(オプション)
-
人間と全く同じことができるのであればただのマンパワーとして考えれば良いが、コンピュータはそうではない。 では、コンピュータに取って都合の良い解決方法があるのだろうか?
そもそも人間の行っている問題解決とは? どうすればそれを工学的に実現できるか?
2. 最急降下法による最適化
コンピュータで解決するには?
どれだけ計算資源を割り当てることができるのか、どれだけ時間資源を割くことができるのかといったコストの観点を捨て去ることはできないが、理想的には、無駄無く適切な解を求めたい。
問題意識: 効率良く最適解(目的物)を探し出すにはどうしたら良いだろうか?
Level2.xでは、解空間が連続値であり、目的関数や制約条件が数式として定義されているという前提で「最適値を効率良く求める」ことについて理解を深めていこう。
- Level 2 : 連続関数における探索手法を検討し、最適性と効率性について考察せよ。
-
Level 2.1 〜 2.3 に示した関数について、最急降下法により最小値を求めるプログラムを作成し、計算機実験により評価し、結果を示した上で考察せよ。
なお、最適解を求める(発見する)にあたり、出発点となる解はランダムに選ばれるものとする。
アルゴリズムの簡単な説明
- 微分値を基に x を移動させる幅を決定する際、「xnext = x -α*f'(x)」により移動先を算出する。学習係数αは 0 より大きい実数とし、この値を変更する事でどのように探索が行われるかを観察せよ。
- 解 x の探索範囲は「-10 <= x <= 10」とする。
サンプルプログラムの利用方法
- サンプルソース:steepestsearch (リポジトリ)
- step 1: ソースのダウンロード。上記URLからダウンロードするか、リポジトリを複製して利用(下記)。
# e1257xxは各自のアカウントを指定すること。 hg clone ssh://e1257xx@shell//net/home/hg/teacher/tnal/steepestsearch cd steepestsearch
- step 2: 各ファイルの説明は 0README_ja.txt を参照。
./0README_ja.txt このファイル. ./Makefile ./steepest-decent.c 探索プログラム本体(これだけ) ./run_ave.sh 10試行時の平均探索回数算出スクリプト。 ./trans_step_vs_func.sh 探索ステップ数あたりの目的関数推移図作成スクリプト。 ./trans_x_vs_func.sh (1変数用)探索時の挙動確認スクリプト。 ./trans_xy_vs_func.sh (2変数用)探索時の挙動確認スクリプト。
- step 3: 目的関数に合わせたプログラム変更。
Level 2.x 毎にプログラム steepest-decent.c を3カ所変更する必要がある。3番目の関数 pdf_y() は2変数時のみ使用する。1変数時には、pd_y()は0を返せば良い。デフォルトでは y=x (Level 2.0) での記述をしている。
- double f(double x, double y): 関数 f(x) or f(x,y) の値を算出するように記述。
- double pd_x(double x, double y): xでの微分値 or 偏微分値を算出するように記述。
- double pd_y(double x, double y): xでの微分値 or 偏微分値を算出するように記述。
- step 4: コンパイル方法。
make コマンド1発でコンパイルできるはずです。エラーがでる場合には編集箇所がおかしい可能性あり。自分で解決できない場合にはTA or 教員に確認してください。
make
- step 5: シミュレーションの実行。
プログラムのコンパイルは make コマンドを実行するのみ。ここでエラーが出なければ ok。実行方法は下記4通りを用意している。
- (1) ./steepest_decent シード値
実行ファイルに直接シード値を指定して実行する方法。Level 2.0 でシード値を1として指定した際の実行結果例。シード値は探索点の初期値を設定するために使用しているため、シード値を変更する度に異なる探索点から出発する。
プログラムの終了条件は3つ。実行結果例ではFINISH 2で終了。
FINISH 1 step ...: 探索回数が term_cond (1000回)を越えた場合。 FINISH 2 step ...: 定義域 (-10 <= x <= +10) を外れた場合。 FINISH 3 step ...: 殆ど探索点が動いていない場合。
- (2) ./run_ave.sh
シード値を千刻み10パターン(1000〜10000)で実行し、FINISH 1〜3で終了した際の平均試行回数を出力。終了条件を3つとも含んでいるため、「最適解を得るために要した平均試行回数」ではない点に注意。
- (3) ./trans_step_vs_func.sh 図タイトル シード値
試行回数(step)あたりの目的関数推移を線グラフで生成。例えば Level 2.1 でシード値1として実行する(下記)とこのような図が作成される。
./trans_step_vs_func.sh "y=x**2" 1
- (4) ./trans_x_vs_func.sh 関数 シード値
探索点が関数上をどのように推移しているかを可視化するスクリプト。例えば Level 2.1 でシード値1として実行する(下記)とこのような図が作成される。
./trans_x_vs_func.sh "x**2" 1 # 実行方法(3)と違い、第1引数は「gnuplotで作図する際の関数そのもの」 # である必要があります。
- (1) ./steepest_decent シード値
注記:レポートには下記4点を含めて報告すること。
- [Level2.1~2.3共通] 探索の手続き、フローチャート。
2.1~2.3で共通している報告事項はまとめて報告すること(同じ報告を繰り返す必要はありません)。
- プログラムソース(スクリプトを含む)。
レポート内には変更個所のみを記載した上で、ソース全体はアップロード提出すること。
- 実行結果。
無駄に全てを示す必要はなく、第三者が読んでも理解できる程度に、必要十分に示すこと。
- 考察。
特に「学習係数が探索挙動に及ぼす影響」として「得られた解の質」と「効率性」について考察すること。 (どう検証したら良いだろうか?)
必要に応じて適切な図表を作成し、理解しやすい考察となるようにすること。
- Level 2.0 : y = x (例題)
-
例題のためレポートには不要です。
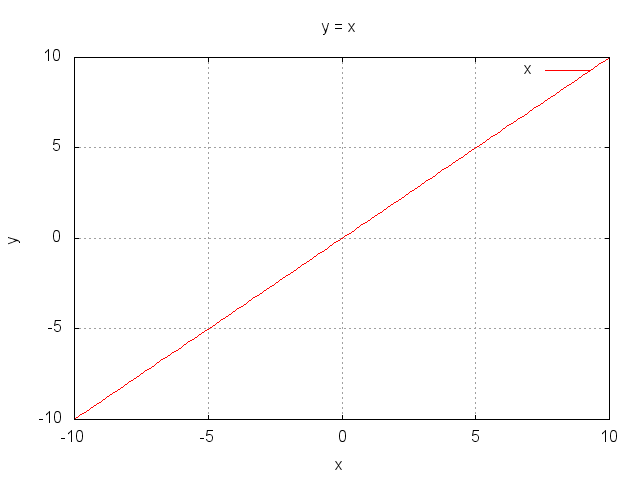
- 実行方法(1)での練習。
- 学習係数 alpha を固定したまま、シード値を変更して実行し、探索動作(出力結果)を確認してみよう。何がどう変わるだろうか?
- シード値を1のままで、学習係数 alpha を変更&コンパイルし直し、探索動作(出力結果)を確認してみよう。何がどう変わるだろうか?
- 実行方法(2)での練習。
- run_ave.sh を使い、最適解を求めるまでに要する平均試行回数を求めてみよう。本当に最適解が得られているかは、以下のようにすると確認しやすい。Level 2.0 の例では十分に x が -10 に近づいていればOK。
tail -1 .archive-*
- run_ave.sh を使い、最適解を求めるまでに要する平均試行回数を求めてみよう。本当に最適解が得られているかは、以下のようにすると確認しやすい。Level 2.0 の例では十分に x が -10 に近づいていればOK。
- 実行方法(1)での練習。
- Level 2.1 : y = x2 (7点)
-
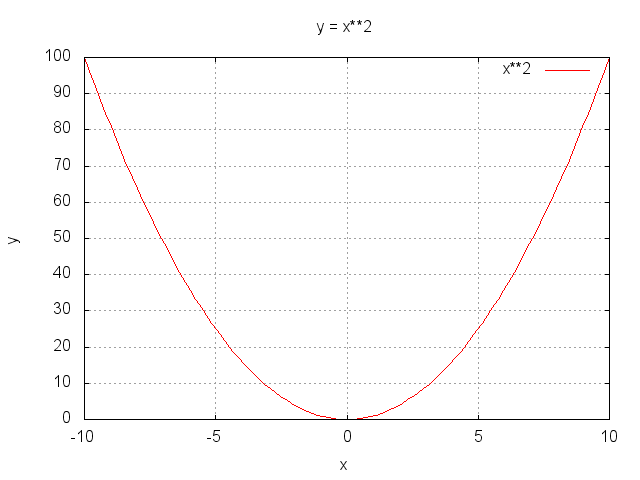
- 「傾きが0となる点」から最適解(最小値となる解)を求めた方が早い例。
- オマケ: (実行方法(3)での練習。)
- trans_step_vs_func.sh を使い、ステップあたりの目的関数推移図を作成してみよう。Level 2.1 の例では、ステップが進むにつれ y 軸が 0 に近づいていくなら正しく収束する方向に探索が進んでいることになる。
- オマケ: (実行方法(4)での練習。)
- trans_x_vs_func.sh を使い、探索点が関数上をどのように推移しているかを可視化してみよう。Level 2.1 の例では、0 に近づいていくなら正しく収束する方向に探索が進んでいることになる。
レポートに含める項目(再掲)
- プログラムソース(スクリプトを含む)。
レポート内には変更個所のみを記載した上で、ソース全体はアップロード提出すること。
- 実行結果。
無駄に全てを示す必要はなく、第三者が読んでも理解できる程度に、必要十分に示すこと。
- 考察。
特に「学習係数が探索挙動に及ぼす影響」として「得られた解の質」と「効率性」について考察すること。 (どう検証したら良いだろうか?)
必要に応じて適切な図表を作成し、理解しやすい考察となるようにすること。
- Level 2.2 : z = x2+y2 (9点)
-
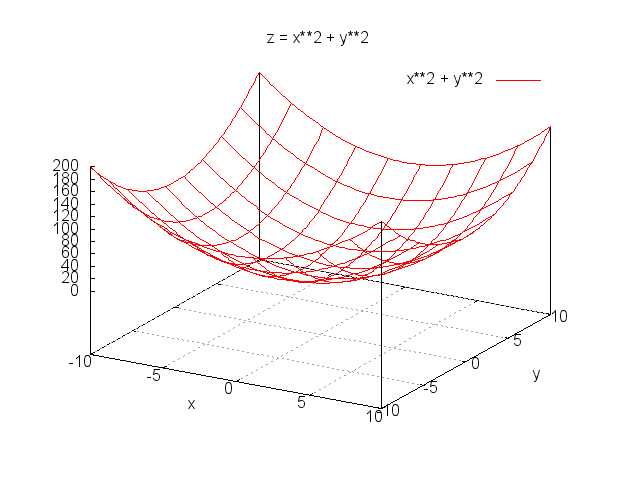
- 目的関数が2変数(x,y)の場合は、pd_y() も修正が必要。pd_x() はxによる偏微分値、pd_y() はyによる偏微分値を返すように記述すること。
レポートに含める項目(再掲)
- プログラムソース(スクリプトを含む)。
レポート内には変更個所のみを記載した上で、ソース全体はアップロード提出すること。
- 実行結果。
無駄に全てを示す必要はなく、第三者が読んでも理解できる程度に、必要十分に示すこと。
- 考察。
特に「学習係数が探索挙動に及ぼす影響」として「得られた解の質」と「効率性」について考察すること。 (どう検証したら良いだろうか?)
必要に応じて適切な図表を作成し、理解しやすい考察となるようにすること。
- Level 2.3 : y = -x*cos(x) (11点)
-
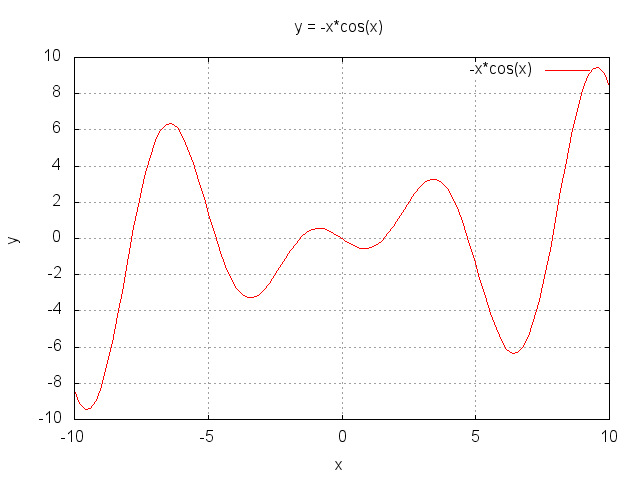
- ランダムな解からスタートするため、多峰の関数においては必ずしも最適解を発見できるとは限らない。このような場合、どのようにしたら最適解を獲得しやすくなるだろうか?
レポートに含める項目(再掲)
- プログラムソース(スクリプトを含む)。
レポート内には変更個所のみを記載した上で、ソース全体はアップロード提出すること。
- 実行結果。
無駄に全てを示す必要はなく、第三者が読んでも理解できる程度に、必要十分に示すこと。
- 考察。
特に「学習係数が探索挙動に及ぼす影響」として「得られた解の質」と「効率性」について考察すること。 (どう検証したら良いだろうか?)
必要に応じて適切な図表を作成し、理解しやすい考察となるようにすること。
- Level 2.x: オプション
-
- 結果の集計・解析ツール(言語は問わない)の作成と利活用。ソースにはコメントを付けること。
- 最急降下法以外の手法を実装する場合には、手法名・概要を説明した上で結果・考察を示す事。オリジナルの手法ならば詳細に説明する事。
3. 最急降下法が苦手とする状況
Level 2.3 で見たように、ノーマルな最急降下法は必ずしもベストな探索手法ではない。Level 3.x に示した不得手な事例では、何が問題で、どのように対策することで改善が見込めそうか? 改善が見込める理由と共に報告せよ。
- Level 3.1 : y = x2+(y2)/10 (9点)
-
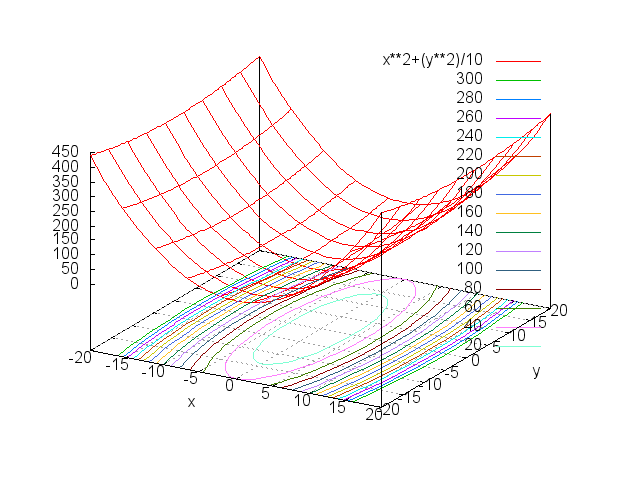
- 「山(谷)」の数は一つにも関わらず、出発点の場所によっては最適解に収束する探索回数が大幅に増えてしまうことがある。
レポートに含める項目(再掲)
- 原因: 何故だろうか?
- 改善(を見込める方法): どうやれば改善できそうか?
- Level 3.2 : y = sqrt(abs(x)) (9点)
-
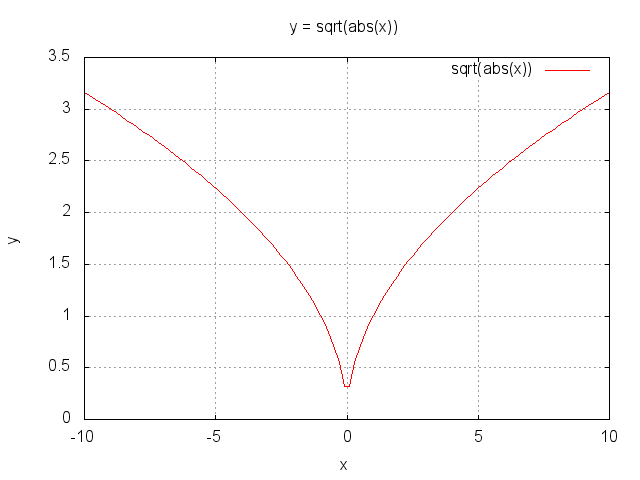
- x=0を境界として微分値の符号が反転するが、正の方向から0に近づいた場合と、負の方向から0に近づいた場合とで極限が異なるため微分可能ではない。「y = abs(x)」でも同様。
レポートに含める項目(再掲)
- 原因: 何故だろうか?
- 改善(を見込める方法): どうやれば改善できそうか?
4. モデル推定時における目的関数の設計
Level2, Level3では目的関数や制約条件が設計済みであり、検討対象は解空間における最適解(や準最適解)の探索手法だけで良かったが、一般的には目的関数等の設計から取り組む必要がある。
- Level 4 : モデルの適切さを図るための目的関数を設計せよ。
-
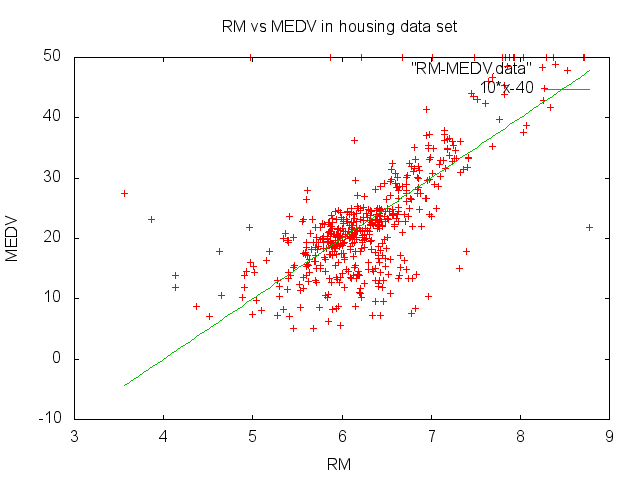
例えば、次のグラフはHousing Data Set(ボストンにおける住宅価格に関するデータセット)から平均部屋数を横軸に、平均価格を縦軸にプロットしている。赤点が実測値を示しており、多くのデータは部屋数に比例した価格になっているように見える。平均部屋数をxとし、この比例関係を*試しに*「価格 f(x)=10*x-40」としてモデル化しようと試みたのが緑の直線である。
問題意識: 上記緑線で描かれたモデルは当てずっぽうで描いたものだが、どのぐらい適切に表現されているだろうか? 言い換えると、「適切さ」を目的関数として設計できないだろうか?
レポートに含める項目
- モデルの適切さを目的関数として設計せよ。目的関数の最大化・最小化どちらで設計しても構わないが、どちらであるかは示すこと。
- どうしてそのような設計を選んだのか、理由を説明せよ。
5. レポート骨組み
レポート作成を分担して進めやすくするために、レポートの骨組みを用意しました。具体的には、input コマンドを用いて複数ファイルを読み込んで、一つのレポートを生成するようにしてあります。分類はあくまでも例ですので、分け方を変更してもらっても構いません。- ダウンロード: reportskel-search1.tgz
- 骨組みをコンパイルして生成できるPDFファイル: search1-utf8.pdf
- コンパイル方法
prompt> make
6. FAQ
- Level1編
- Q: Level1.2の具体事例として「hogehoge(何かしらの新機能)」を提案したら何でも良いのですか?
- A: 「探索」という観点で考察できるならOK。
- Level2編
- Q: 実行方法(4)の trans_x_vs_func.sh がうまく動かない。
- A: 第1引数は「gnuplotで作図する際の関数そのもの」を入力してください。例えば以下では y = x*x で、シード値1とする際の例を示しています。
./trans_x_vs_func.sh "x**2" 1 # 実行方法(3)と違い、第1引数は「gnuplotで作図する際の関数そのもの」 # である必要があります。
- Q: gnuplotでエラーがでる。or 実行方法(3)~(4)で図が作成されない。
- A: gnuplotが利用しているライブラリを次のコマンドで調べることができる。
otool -L `which gnuplot`
今回のシェルスクリプトではset terminal pdf(libpdfを利用)を指定しているが、インストールしているgnuplotの状態によってはそもそもlibpdfを組み込んでいないか、gnuplot本体との整合性が取れていないために作図時にエラーが出てしまうことがある。この場合には、次のようにシェルスクリプトを変更して作図しよう。- (1)set terminal を「postscript」に変更。
- (2)set output で保存するファイル名の拡張子をps or epsに変更。
- Q: 実験中のグループ活動で何をやって良いのか分からない。
- A: サンプルプログラムは「最急降下法で y=x における最小値を探索する」ように書かれています。そこで、まずはLevel2.1なり問題を選択して、その問題を解くようにプログラムを修正する必要があります。
[step1] プログラムの修正
まずはLevel2.1, 2.2, 2.3どれでも良いので一つ選択し、選択した関数におけるy=f(x)とy'=df(x)に書き換えて動作するようにしましょう。適切に動いているかは「xとyの関係」だけで判断できるはずです。
[step2] パラメータを変更して動作観察
想定した関数上で探索が進んでいることを確認したら、alphaやseedを変更して探索動作がどのように変わるかを観察しましょう。どちらを変更するかは「何を観察したいか」で選ぶことになります。alphaは「探索点の移動幅を調整するパラメータ」です。seedは「初期探索点を選ぶためのパラメータ」です。移動幅を大きくした時に探索点の移動がどのように変わるかを観察したいのならalphaを選択(変更)するべきでしょう。出発点を変えたときにどのように探索動作が変わるかを観察したいならseedを選択(変更)するべきでしょう。いきなり複数のパラメータを変更してしまうと、どちらのパラメータがどのように影響しているかを観察することが難しくなるため、一般的には「一つのパラメータの影響」を観察している最中は他のパラメータを固定しておき、観察対象のパラメータだけを少しずつずつ変更していき、傾向を探ることになるでしょう。今回は「最適性」と「効率性」という視点で考察できるように実験計画を練ってみてください。
- 参考文献・サイト
-
- 口頭試問調整用の記事
- 情報工学実験2/探索アルゴリズム1の口頭試問日調整(後でURLを書き直します)
- スクリプト等、実験環境関連
- google keywords: perl, ruby, gnuplot
- 実験1: Shell script と gnuplot の参考文献・サイト
- Gnuplot入門
- 探索関連
- google keywords: 探索、最適化、連続関数、微分、不連続関数、近似解法
- AI リンク集@人工知能学会
- 人工知能のやさしい説明「What's AI」@人工知能学会
- 非線形計画法@電気電子工学科・半場先生
- MovieLens
- MovieLens Data Sets(GroupLens Research)
- 集合知プログラミング 2章 その11 MovieLensのデータを使った推薦をしてみる
- UML
- その他
- 口頭試問調整用の記事