1 はじめに

　マルチエージェントシステムの構成において適応アルゴリズムの有効性が指摘されている. 免疫アルゴリズム(Immune Algorithms; 以後, IA)[1,2]は人間の免疫機構を模倣した適応アルゴリズムの一種であるが, その有効性及び工学的応用に関する可能性はまだ十分に議論されていない.

　本稿では,免疫システムの多種多様な抗原(環境)への対応能力に着目し,その有効性を見るため, マルチエージェンントシステムの代表的な問題の一例である分業巡回セールスマン問題(n-Traveling Salesman Problem; 以後, nTSP)[3]への適用を行なう.

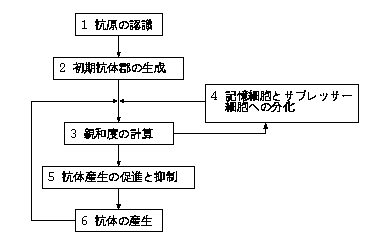
　免疫システムとは, 生体内に侵入する非常に多くの未知の抗原に対応するために, 細胞遺伝子の再構築を行なって抗原に対応する抗体を産生し, 抗原を排除する機構である.本稿では, 森らによって提案された免疫アルゴリズム[1]を採用する. IAを図に示す．

図１：免疫アルゴリズム

3.1 nTSPの特徴

　マルチエージェントシステムは各エージェント間の協調により効率の良い問題解決を行なうことを目的とした枠組である．一方，nTSPはTSPをn人セールスマンに拡張することにより，都市の巡回を効率良く行なうことを目的とする問題であることから， マルチエージェントシステムが解決すべき問題の典型例となっている．

　nTSPは本質的に各セールスマンに対する都市配分とその最短経路探索という2面性を持ち, これらはともにNP完全問題である.また, これらの2面性は相互に関連しているため個別に逐次的に解くことが困難である．

　免疫システムは複数の環境に対する適応能力があるためこのような問題への有効な問題解決手法であると考えられる． 以下にnTSPのIAによる解法を示す.

3.2 nTSPの免疫システムにおける解法

目的：

各セールスマンのパス（都市を巡回する順序）の合計（コスト）を最小にするようなプランを探索する.

制約条件：

各セールスマンのパスは出発都市(=最終都市)を同一とする.また, 各パスの出発都市以外の都市は他のセールスマンのパスに含まれない.

以下に本稿で使用する記号及び関数を説明する.

n	セールスマン数
m	都市数
dij	都市iから都市jへの距離
(xi, yi)	各都市位置の座標
Si	セールスマンi
PSi	セールスマンiのパス
Plank	1巡回計画

[目的関数]　min ( cost_k = Σf_d(P_Si) 　　　　　　(1)

式(１)で, P_SiはセールスマンS_iのパスで,出発都市と最終都市を除いたパスである. f_dはS_iの距離の総和を求める関数である.

[制約条件]　P_Si ∩ P_Sj = Φ, 　i ≠ j 　(∀ i, j)　(2)

式(２)はセールスマンiとjのパス上に都市の重がないことを意味する制約条件である.

Plank =

ts	PS1	ts
ts	PS2	ts
：	：	：
ts	PSn	ts

式(３)の各行は各々のセールスマンのパスを表しているプランである. P_S1はセールスマンS₁のパスを意味する.

　nTSPの解をIAで求めるためには, 問題の抗体を文字列で表現しなければならない.

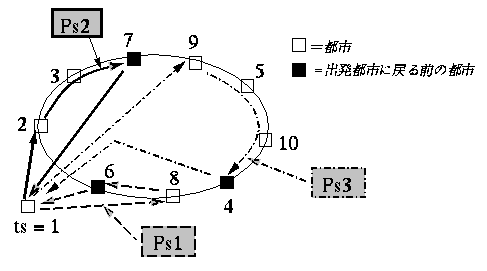
図２：nTSPの解のイメージ

図１は, 都市数m=10, セールスマン数n=3に置ける1プランの概念図を表している. コーディングではGAと同じように,1プランの情報を遺伝子(抗体)に持たせる必要がある. 同図より抗体情報には各セールスマンのパス(P_Sn), 及び各パスの大きさ(|P_Sn}|)を文字列表現すれば良いことがわかる.この2つの情報を順序表現[4]によりコーディングを行なった. 図２は図１に置けるコーディング例である.

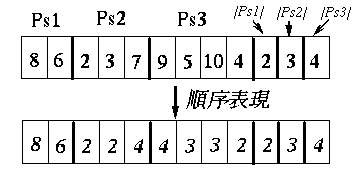
図３：コーディング例

　

　適応アルゴリズムの一手法である免疫アルゴリズムをマルチエージェントシステムの典型問題であるnTSPへ適用し，その工学的応用に対する可能性について検討した．免疫アルゴリズムはマルチエージェントシステムにおける有力な問題解決手法と考えることが出来る．

[1]　森 ,築山 ,福田 :免疫アルゴリズムによる多峰性関数最適化,T.IEE Japan, Vol.117-C, No.5, 1997.

[2]　和田 健之介,和田 佳子,山登り飛び虫の進化と免疫システム論について, 数理科学,NO.353, NOVEMBER, 1992

[3]　中村 ,角田 ,田中 :分業セールスマン問題のニューラルネットワークによる解法, 情報処理学会 人工知能研究会資料 94-2, (1994, 6, 20)

[4]　J.Grefenstette, R.Gopal, B.J.Rosmaita and D.Van Gucht :Genetic Algorithms for the Traveling Salesman Problem, Proc. of ICGA '85, 16/168 (1985)

・一つ前のページ(原稿集)に戻る

・ホームページへ戻る