In the AI field, adaptive algorithms such as neural networks or genetic algorithms are recognaized as the powerful learning systems or effective search methods. However, about immune algorithms modeled as a human immunity, it's fundamental ability and engineering applicablity is not cleared yet. In this paper, we apply the immune algorithm to the n-th traveling salesman problem (n-TSP) and discuss the effectivity of this algorithm.
自律系システム、適応系システム、調和系システムなどのインテリジェントシステムの設計構成において、ニューラルネットワーク、遺伝的アルゴリズムなどに代表される適応アルゴリズムの有効性がさまざまな研究成果により指摘されている。一方、生体系に内在するインテリジェントシステムである免疫系についての工学的応用に関する可能性及びその有効性は十分に議論されているとは言えない。
本稿では,免疫システムの抗原の認識機構、抗体の記憶機構、抗原の排除機構に着目し, その工学問題に対する有効性を検討するために,マルチエージェントシステムに対する最適化問題の一例である分業巡回セールスマン問題(n-Traveling Salesman Problem; 以後, nTSP)へ適用し、アルゴリズムの性能、特徴について検討する。また,だまし問題を通して記憶機構の利用に関する考察を行なう.
2.1 TSPとnTSP
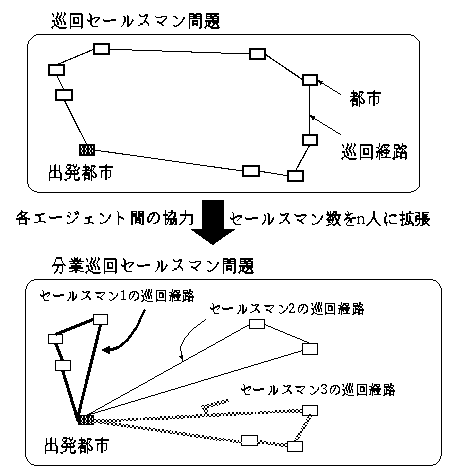
巡回セールスマン問題TSPはNP-hardに分類される問題の複雑さとその応用範 囲の広さからさまざまな解法による検討がなされてきた。しかし今日の大規模複 雑な工学的諸問題への対応には各エージェント間の協力による効率良く問題を解 決を行なうマルチエージェントシステムなどのより強力な問題解決法が求められ ている。そこでTSPにおけるエージェント数をn人に拡張した nTSP問題[4]を設定し、マルチエージェント型アルゴリズムの性能評価の基準問題として位置付ける(図1)。
nTSPは本質的に各セールスマンに対する都市配分とその最短経路探索という2面性を持つ。これらの2面性は相互に関連しているため個別に逐次的に解くことが困難であるという特徴を持つ。免疫システムでは動的な環境に対する適応能力が期待されるためこの種の問題に対し有効な問題解決手法であると考えられる.

2.2 nTSPの定式化
Table1に本稿で使用する記号を示す.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nTSPにおいて目的は各セールスマンのパス(都市を巡回する順序)の合計(コスト)を最小化するようなプランを作成することである。付随する制約条件は
[目的関数]
min ( costk = Σi fd(PSi) )…(1)
式(1)で, PSiはセールスマンSiのパスで,出発都市と最終都市を除いたパスである. fdはSiの距離の総和を求める関数である.
[制約条件]
PSi ∩ PSj = φ, i ≠ j (∀ i,j)…(2)
式(2)はセールスマンiとjのパス上に都市の重複がないことを意味する制約条件である.
Plank =
…(3)
ts
PS1
ts
ts
PS2
ts
:
:
:
ts
PSn
ts
式(3)の各行は各々のセールスマンのパスを表しているプランである. PS1はセールスマンS1のパスを意味する.
免疫システムとは, 生体内に侵入する多種多様な未知の抗原に対応するために, 細胞遺伝子の再構築を行なって抗原に対応する抗体を産生し, 抗原を排除する生体監視防衛機構である.
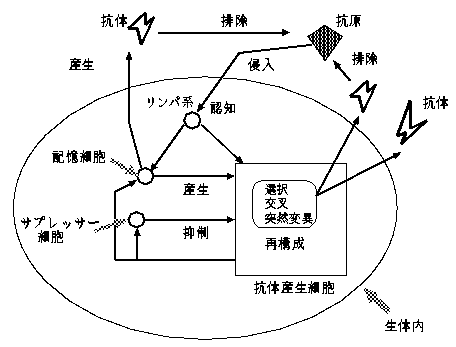
工学的応用の一例に森らによってモデル化された免疫アルゴリズム[1,2]がある。本稿ではそのアルゴリズムの基本構成に従う。
[Step 1] 抗原の認識
抗原を入力情報として認識する.
[Step 2] 初期抗体群の生成
記憶細胞から過去に有効であった抗体群を生成する.
[Step 3] 親和度の計算
抗原と抗体vの親和度axvと抗体vと抗体wの親和度ayv,wを計算する.
[Step 4] 記憶細胞とサプレッサー細胞への分化
全ての抗体の濃度を計算し, 抗体vの濃度cvが閾値Tcを越えた場合に, 抗体vを記憶細胞mに分化させる. また, 新しく分化した記憶細胞と同じ遺伝子を持つサプレッサー細胞sを分化させ, サプレッサー細胞との親和度が, 類似度の閾値以上の抗体を消滅させる.
[Step 5] 抗体産生の促進と抑制
次世代に残る抗体vの期待値evを計算し, 現世代の抗体の親和度の低いもののいくつかの抗体を消滅させる.
[Step 6] 抗体の産生
4で消滅させた抗体に変わる新しい抗体を, 乱数を用いてその遺伝子をランダムに決定することによって産生する. 以下, 世代があらかじめ設定した最終世代に達するまで3〜6を繰り返す.
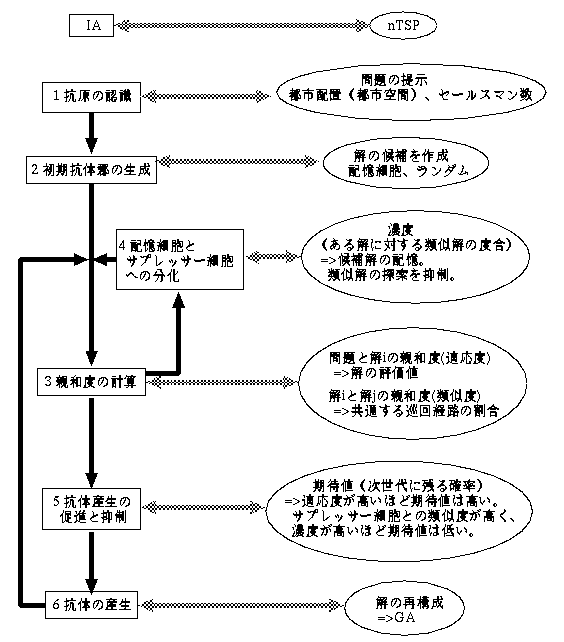
免疫アルゴリズムはその基本構成を(1)遺伝的アルゴリズムに基づく解の再構 成(2)記憶細胞による有効解の記憶(3)サプレッサー細胞による記憶解の再探索の 抑制とする。この構成によりGAの持つ強力な広域な探索能力に加え、有効解の再 利用及び再探索の抑制による探索効率の上昇が期待される。以下に免疫アルゴリ ズムの処理手順とnTSPとの関係を示す(図3,図4)。

4.1 コーディング
nTSPにIAを適用するためには, 問題の抗体を文字列表現しなければならない.
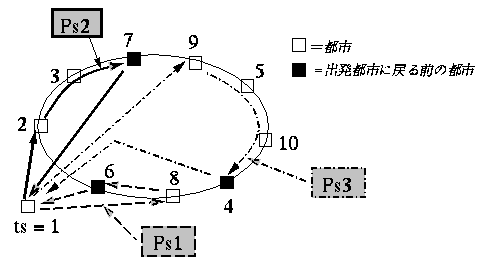
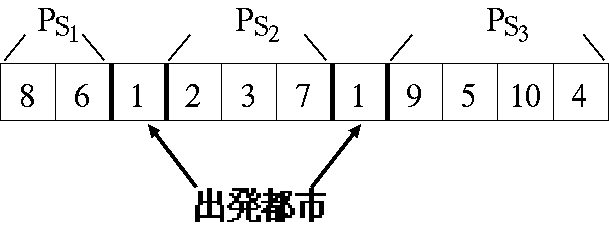
図5は, 都市数m=10, セールスマン数n=3に置ける1プランの概念図を表している.1プランの情報を染色 体(抗体)に記述する必要がある.GAによるTSPの一解法としてGrefenstetteによ る 順序表現[5]がある。nTSPでは抗体情報をnセールスマンに分割しなければならないためそのコーディング法に分割情報を加え拡張した。染色体に分割情報であるセパレータを加えたコーディング例が図6である。
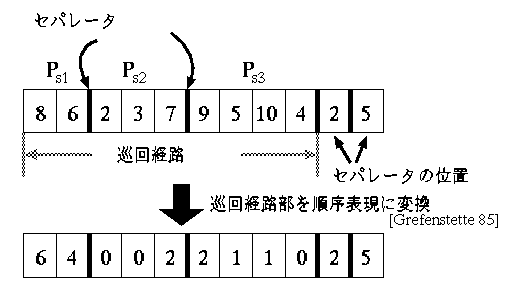
図6では、(1)各セールスマンのパス(PSn)とnセールスマンに分けるためのセパレータの位置を文字列表現し、(2)各セールスマンのパス部分(巡回経路部)を順序表現することでコーディングを施した例である。
4.2 各評価尺度の計算
免疫アルゴリズムにおいては、適応度、類似度、濃度、期待値の4つの計算尺度を求める必要がある。以下にnTSPにおける評価尺度の計算式を定義する。
ここで,penaltyは一プランにかかるコスト(work)の平均と各セールスマンの巡回経路コストの差の総和を計算している.また本稿では,ここで挙げた尺度をnTSPと関連させて,適応度を解の評価値,類似度を2つの解に共通する巡回経路の割合,濃度をある解が集団を支配する割合,期待値を次世代に残る確率として扱うことにする.
5.1 実験1
実験1では,nTSPに対しIAが有効に機能するかどうかを確認する.設定する問題は都市数12,セールスマン数4とし,都市配置は出発都市を中心に円周上に配置した.IAの各パラメータはTable2のように設定した.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
サプレッサー細胞の総数 |
|
|
|
|
ここで,交叉確率1及び突然変異確率1は巡回経路部における確率であり,交叉確率2及び突然変異確率2はセパレータ部における確率を意味する.本稿で取り扱うコーディングでは分業に関する情報がセパレータ部のみにあるため,巡回経路部よりもセパレータ部の操作確率を高く設定した.
遺伝子の再構成に使用するGAのオペレータは以下のように設定した.
図6は初期集団内のプランの一例であり, 図7はIAによって得られた最適解である.
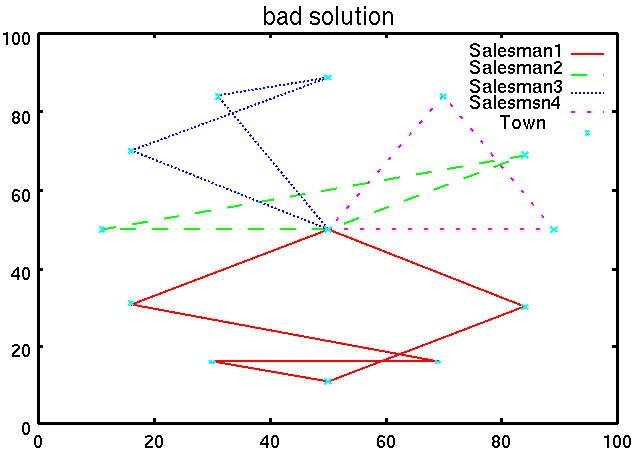
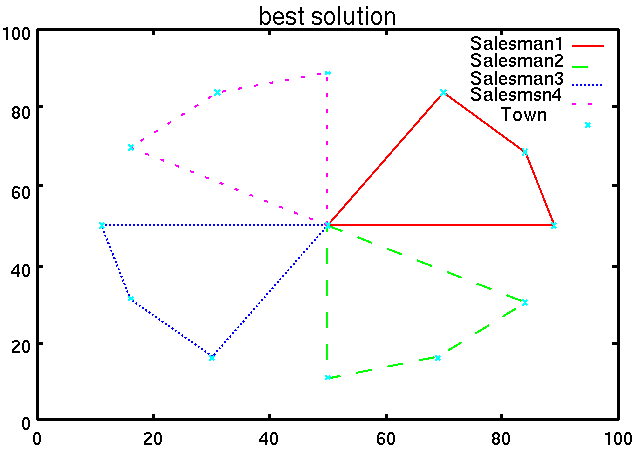
これらの図から,IAが適切なnTSPに対するプランを作成可能であると考えられる.
5.2 実験2
実験2では,IAの探索効率を評価するためにSimpleGAとの比較を行なった.比較に用いた問題はセールスマン数2,都市数10とし,ランダムな都市配置を30題用意した.また,IAとGAの各パラメータは,Table3のように設定した.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
実験結果を図8に示す.
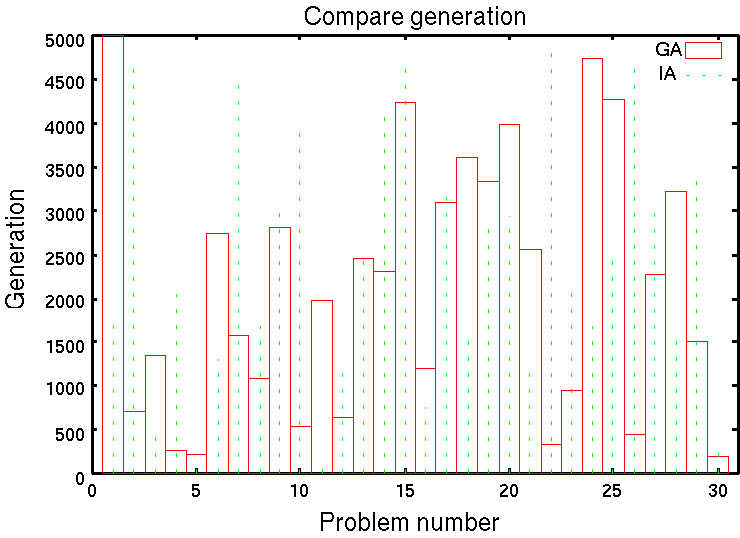
図8は,横軸に問題番号,縦軸に世代数をとり,boxがGA,lineがIAを示している.グラフから,30題に対する準最適解探索までの世代数比較では,GA:IA=13:17でIAが優位であることが分かる.また,問題11では,IAがGAと比較して極めて早い世代で準最適解を獲得している.これはIAが過去に探索した候補解を記憶し,利用することで,類似性の高い問題に対して,効果的に準最適解を求めることができることによると考えられる.このことは,生体系における実際の免疫システムが一度記憶した抗原に対し適切に反応し,自己防衛を行なう行動様式に一致する.
6.1 記憶の利用
探索中の候補解の記憶は,式(6)で計算した濃度がある閾値を越えた時に行なう(図9).
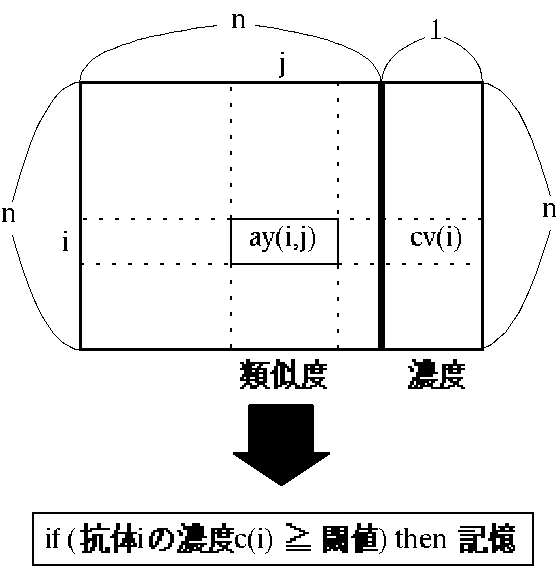
本稿では閾値を越えた解そのものを記憶細胞とサプレッサー細胞に記憶している.
記憶細胞の総数mに達したら,今保存しようとしている解と最も類似度が高い記憶細胞と交換する.
サプレッサー細胞の総数sに達したら,最も古いサプレッサー細胞と解を交換する.
このように記憶された結果,記憶細胞では探索中における局所解を保存し,サプレッサーでは常に記憶細胞に記憶されたばかりの解を保存するはずである.このため,局所解を最適解に持つような類似問題に対しては記憶細胞の再利用により探索を用意にすると考えられる.また,局所解を記憶したなら局所解に類似する解を再探索することは無駄であると考えられるため,サプレッサー細胞に記憶された解に対する類似解の探索を抑制する.しかし,記憶された解が局所解になっているかどうかは分かり得ないため,サプレッサー細胞の総数を少なくすることにより後々には再探索する可能性があるように実装を行なった.
現在の仕様では,記憶細胞の適応度を新しい問題に対して計算し,適応度の高い記憶細胞で初期集団の半数程度を構成し,不足分をランダムに作成することで記憶細胞の再利用を行なっている.記憶方法及び,記憶の再利用方法にはまだ検討の余地が残っているが,本稿では類似問題について考察することにする.
6.2 だまし問題
だまし問題は2重の同心円上に同数の都市が均等に並んだ都市配置を扱い,そ の内外円の半径比によって2通りの大きく異なる最適解,局所解を持つ.図10は どちらか一方の円を巡回してからもう片方を巡回するプラン(c-type)が最適解と なる例で,図11は外円と内円を交互に巡回するプラン(o-type)が最適解となる例である.
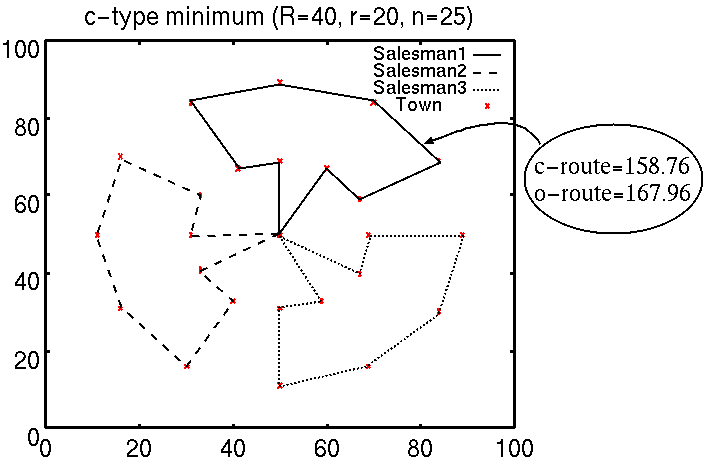
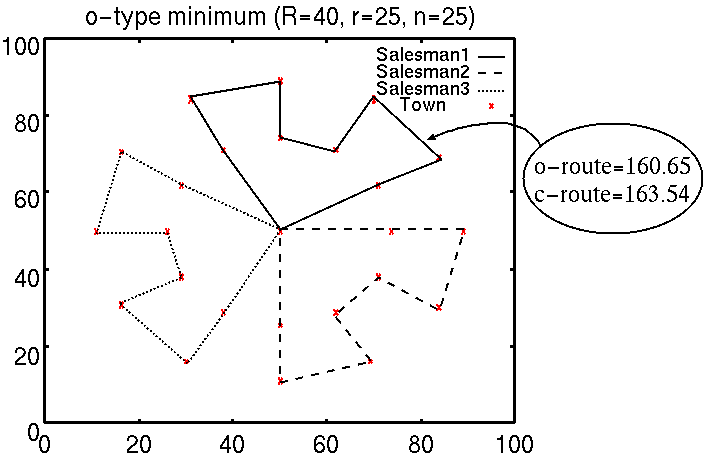
このように大きく異なる最適解,局所解が存在するだまし問題においてはIAの記憶細胞を再利用することにより探索が容易になると考えられる.
7.1 問題設定
実験3では,類似問題としてだまし問題を設定し,記憶の再利用により探索が容易になることを確かめる.確認方法は以下のように行なう.
IAの記憶細胞を構成させるため,記憶細胞なしでc-typeが最適になる問題を解く.
Step1で得られた記憶細胞を再利用し,異なる順路o-typeが最適解となる問題を解く.
Step1で得られた記憶細胞を再利用し,同じ順路c-typeが最適解となる(Step1で解いた問題とは異なる)問題を解く.
Step1-3の探索の様子を比較する.この時,Step1よりもStep2,3の方が探索効率が上昇しているならば探索が容易になっていると考えられる.以下ではStep1をCempty(記憶なしでc-typeを解く),Step2をOc(c-typeの記憶を利用してo-typeを解く),Step3をCc(c-typeの記憶を利用してc-typeを解く)と表記する.
各Stepで探索する問題はTable4のように設定した.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
外円と内円上には6都市ずつ,出発都市を円の中心に配置した. IAのパラメータはTable5のように設定した.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ここで,類似度の閾値は類似度の計算,濃度の閾値1は濃度の計算,濃度の閾値2は記憶する際の閾値にそれぞれ使用する.
7.2 実験結果
実験3の結果を図12,図13に示す.
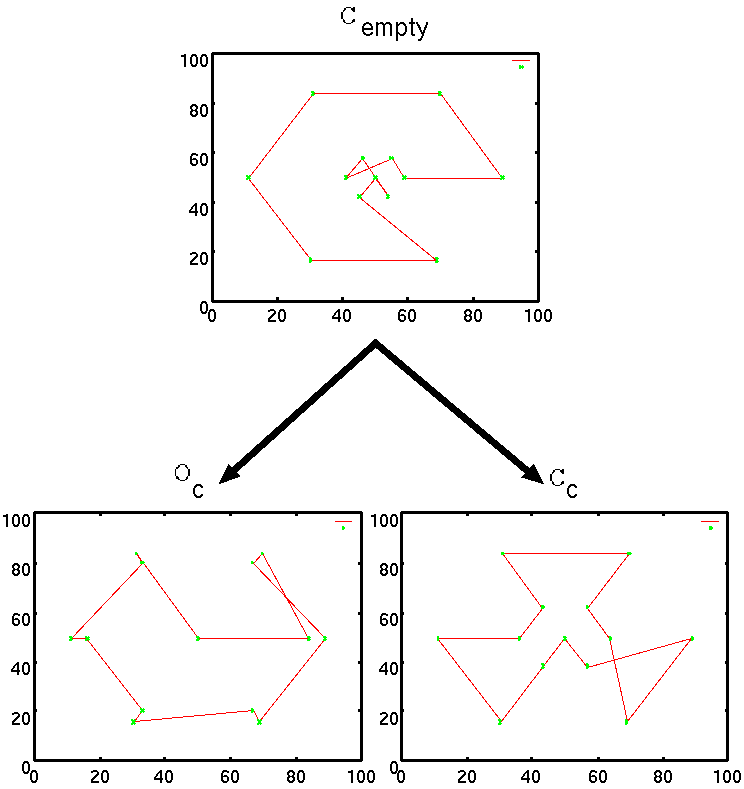
図12はそれぞれ,Cempty(同図上),Oc(同図左下),Cc(同図右下)の探索で得られた最良解を図示している.
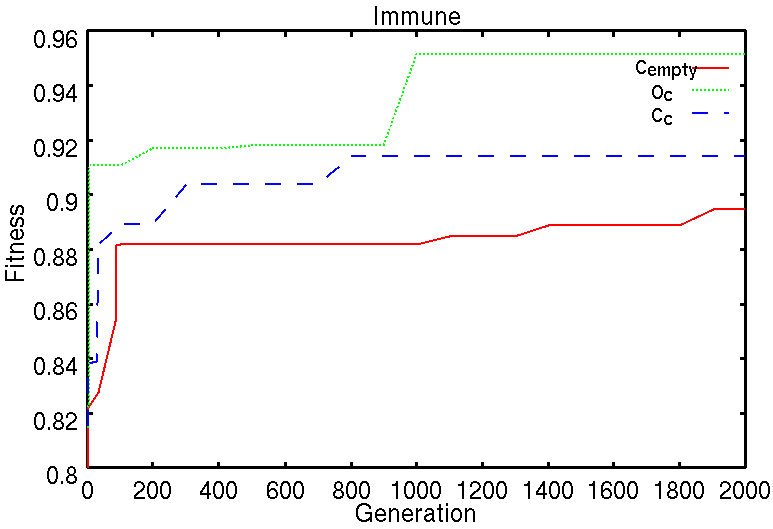
図13は実験3で扱った3問題の探索効率を比較している.縦軸は最適解を1としてスケーリングした適応度,横軸は世代数を表している.同図より,100世代までの適応度の上昇率を比較すると
の順に良くなっていることが分かる.今回の実験では最適解を探索できていないために断言することは出来ないが,類似問題の探索において過去の記憶を利用することで容易にできると考えられる.
8.1 濃度と順序表現
現在の実装では,大きな問題空間に対しては探索がうまくいかなかったため,実験3のように問題空間を狭めて実験を行なった.IAにはある解が集団を支配する割合(濃度)が高くなるとその解を候補解として記憶するが,濃度が高くなるためには前世代の形質を保存する必要がある.しかしながら,本稿で用いた順序表現によるコーディングは,交叉操作における致死遺伝子作成の問題を解決することを主眼に作られた手法であるため,形質が保存されにくい.濃度と順序表現という目的の相反する組合せを取ってしまったため前述した問題点が出てきたと考えられる.
8.2 濃度とパス表現
濃度は表現型における類似度から計算される.そこで表現型を直接コーディングしたパス表現を用いることにする.図5をパス表現でコーディングした例が図14である.
TSPにおいては,パス表現された遺伝子に通常の交叉操作を行なうと致死遺伝 子を作成しやすくなるため特別な交叉操作を使用することになる.そこで形質の 保全にマッチした サブツアー交換交叉[6]を採用する方向で考えている.
適応アルゴリズムの一手法である免疫アルゴリズムをnTSPへ適用し,その工学的応用に対する可能性について検討し,計算機実験によりその有効性について示した.また,類似問題としてだまし問題を取り上げ,探索を容易にできる可能性があることを示した.特に,記憶機構を活用することで,動的環境における類似問題の繰り返し解決を必要とする課題に対して有効に機能すると考えられる.複数の問題解決器を基本とするマルチエージェント系の有効なアルゴリズムとしてのIAの利用が期待される.
[1] 森 一之,築山 誠,福田 豊生,多様性を持つ免疫的アルゴリズムの提案と負荷割り当て問題への応用, T.IEE Japan, Vol.133-C, No.10, 1993.
[2] 森 一之,築山 誠,福田 豊生,免疫アルゴリズムによる多峰性関数最適化,T.IEE Japan, Vol.117-C, No.5, 1997.
[3] 和田 健之介,和田 佳子,山登り飛び虫の進化と免疫システム論について,数理科学, NO.353, NOVEMBER, 1992
[4] 中村 友洋,角田 達彦,田中 英彦,分業セールスマン問題のニューラルネットワークによる解法, 人工知能 94-2, (1994, 6, 20)
Back[5] J.Grefenstette, R.Gopal, B.J.Rosmaita and D.Van Gucht : Genetic Algorithms for the Traveling Salesman Problem, Proc. of ICGA '85, 16/168 (1985)
Back[6] 山村 雅幸,小野 貴久,小林 重信,形質の遺伝を重視した遺伝的アルゴリズムに基づく巡回セールスマン問題の解法,人工知能学会誌,Vol.7, No.6, Nov. 1992
Back
・ホームページへ戻る