マルチエージェントシステムの構成において適応アルゴリズムの有効性がさまざまな研究成果により指摘されている.免疫系は生体内に内在するインテリジェントシステムであり,その工学的応用に関する研究が進められている.
本研究では,免疫システムの抗原の認識機構,抗体の記憶機構,抗原の排除機構に着目し, その工学問題に対する有効性を検討するために, マルチエージェントシステムに対する最適化問題の一例である分業巡回セールスマン問題(n-Traveling Salesman Problem; 以後, nTSP)[4]へ適用し,免疫アルゴリズムの性能,特徴について検討する.
==> 最初に戻る
TSPにおけるエージェント数をn人に拡張したnTSP問題を設定し,マルチエージェント型アルゴリズムの性能評価の基準問題として位置付ける.nTSPは以下のような2面性を持つ.
それらは相互に関連しているため個別に逐次的に解くことが困難であるという特徴を持つ.
目的関数と制約条件は以下のようになる.
式(1)で, PSiはセールスマンSiのパスで,出発都市と最終都市を除いたパスである. fdはSiの距離の総和を求める関数である.
[制約条件] PSi ∩ PSj = φ, i ≠ j (∀ i, j) (2)
==> 最初に戻る
工学的応用の一例に森らによってモデル化された免疫アルゴリズム[1,2]がある.

免疫アルゴリズムの基本構成を以下に示す.
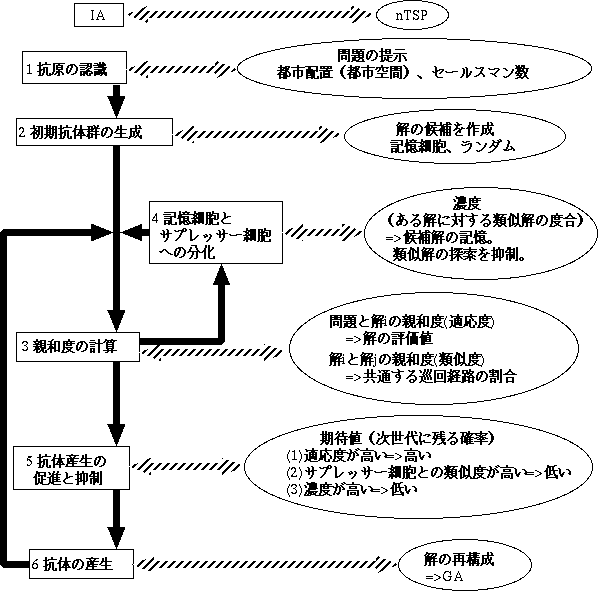
この構成によりGAの持つ強力な広域な探索能力に加え,有効解の再利用及び再探索の抑制による探索効率の上昇が期待される.図1に免疫アルゴリズムとnTSPの関係を示す.
==> 最初に戻る
IAでは類似度の概念が重要である.そのため,類似度を効率的に計算できるコーディング,またそのコーディングに適した遺伝子操作オペレータを設定することが必須である.
本研究では,nTSPにおける類似度を巡回経路の共通性として捉える.そこで,コーディングにはその共通性を計算しやすいパス表現を用いる.交叉操作には,解の形質の保全を重視したサブツアー交換交叉[5]を用いる.また,任意の2都市を交換する突然変異操作を用いる.
==> 最初に戻る
IAにおいては,4つの計算尺度を求める必要がある(図1).以下にnTSPにおける評価尺度の計算式を定義する.
==> 最初に戻る
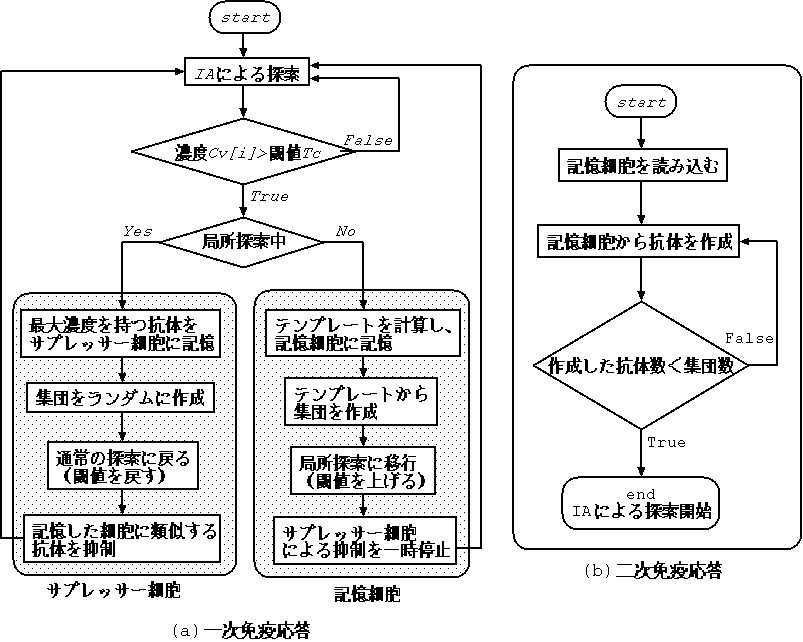
記憶の利用方法として,一次免疫応答と二次免疫応答(図2)を提案する.また,記憶細胞に記憶するデータとして,集団中の抗体の特徴を表すと考えられるテンプレートを用いる.各々の免疫応答の狙いは以下の通りである.
 >
>
==> 最初に戻る
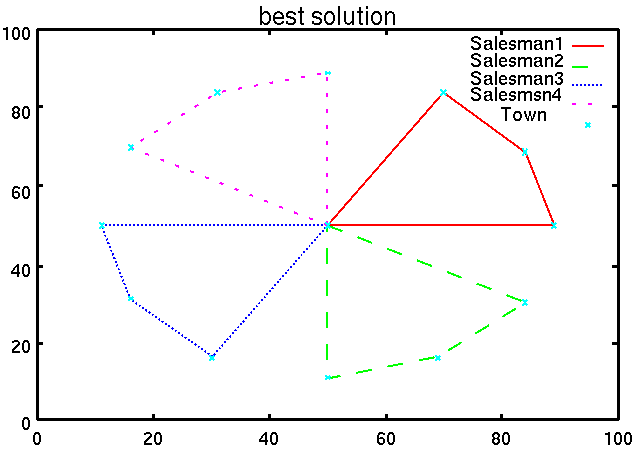
都市数13,セールスマン数4という問題設定で実験を行なった.実験結果は図3のように,nTSPの最適解をIAにより得られることが確認できた.
==> 最初に戻る
実験2では,IAの探索効率を評価するためにsimpleGAとの比較を行なう.比較に用いた問題はセールスマン数2,都市数10とし,ランダムな都市配置を30題用意した.
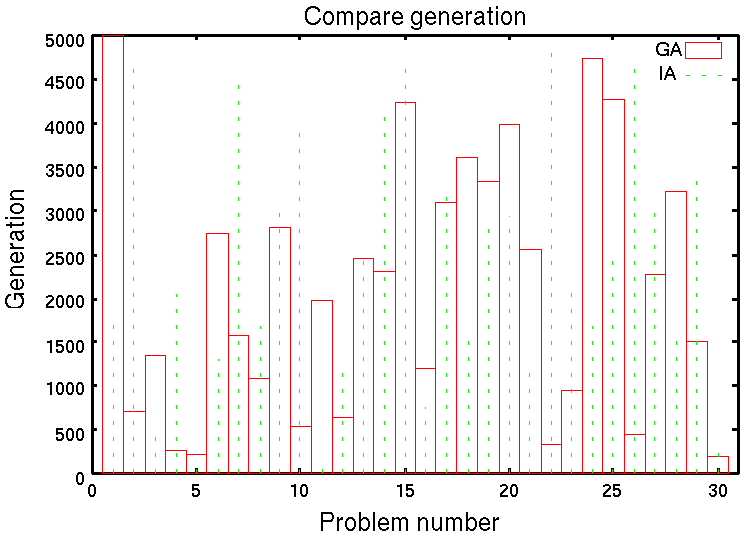
実験結果を図4に示す.同図において,30題に対する準最適解探索までの世代数比較では,GA:IA=13:17でありほぼ同等であった.しかしながら,問題11では,IAがGAと比較して極めて早い世代で準最適解を獲得している.これはIAが過去に探索した候補解を記憶し,利用することで,類似性の高い問題に対して,効果的に準最適解を求めることができることによると考えられる.
==> 最初に戻る
実験3では,3.3節で提案した一次免疫応答と二次免疫応答の有効性を確認することを目的とする.ここでは,二重の同心円上に同数の都市が均等に並んだ都市配置であるだまし問題を扱う.だまし問題は,同心円の半径比によりc-typeまたはo-typeのどちらか一方を最適解,他方を局所解に持つ類似問題である.c-typeとはだまし問題における一方の円を巡回してから他方を巡回するプランである.o-typeとは外円と内円の弧を交互に巡回するプランである.
確認方法は,一つの問題に対し,以下の5種類の記憶の利用方法における適応度の上昇率等の比較により行なう.
ここで,記憶を作るために用いる問題(c-typeとo-typeと書く)とその後に解く問題(c'-typeとo'-typeと書く)を表~\ref{problem-memory-solve}に示す.同表におけるc-typeとはc-typeが最適解となる問題を意味する.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
==> 最初に戻る
実験結果を図5に示す.同図において,empty=記憶なし,c=c-typeの問題を解いた時の記憶,o=o-typeの問題を解いた時の記憶,co=o-typeの次にc-typeを解いた時の記憶のそれぞれを利用した探索を意味する.図5より,記憶を利用することで,最適解を得るのに要する世代数を減少できる場合があることがわかった.また,適応度の上昇率を見ると,記憶なしで探索を行なうよりも同種の類似問題を過去に探索した記憶を用いた方がより上昇度が高いことがわかる.
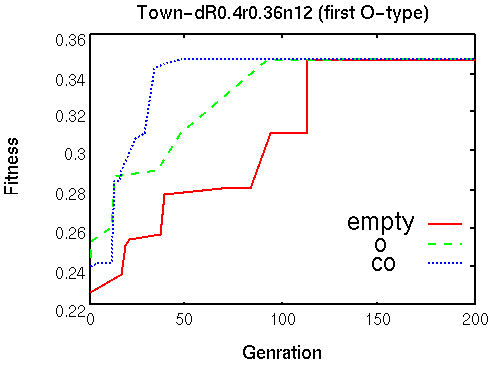
最適解を得た世代数は表2のようになっており,単に同種の問題を解いた記憶oだけよりも,異種の問題を解いた記憶coの方がより早い世代で最適解が得られた.
|
|
|
|
|
|
|
|
|
|
以上の結果から,c-typeを後に解きたい場合には予めc-typeを解くことで記憶を作成しておく.o-typeの場合にはその逆をすることが有効であると考えられる.また,ここで用いた記憶の解析を行なったところ,最適解を得ることができた記憶o及び記憶coに関しては,o-typeの問題に対して有効に働くテンプレートが記憶されていたことが確認できた.
==> 最初に戻る
適応アルゴリズムの一手法である免疫アルゴリズムをTSPへ適用し,その工学的応用に対する可能性について検討を行なった.また,記憶の利用方法として一次免疫反応と二次免疫反応の導入を提案し,計算機実験を行なった.その結果から,記憶機構を活用することで動的環境における類似問題の繰り返し解決を必要とする課題に対して有効に機能する可能性があることがわかった.一方,記憶機構を有効に活用する方法にはまだ改善の余地があると考えられる.
==> 最初に戻る
==> 最初に戻る
ホームページへ戻る