前回2の補数表現された8ビットの数の平均を計算する回路を設計し、加算器を使用しました。今回は乗算器を設計します。
8ビットの2の補数表現の最小値、最大値は以下のようになります。
| 8ビットの2の補数 | 10進数表現(整数表現) | |
| 最大値 |
0111 1111 |
127 |
| 最小値 |
1000 0000 |
−128 |
したがって、−128から127の間の整数が表現されます。
8ビットの2の補数表現表現された数を乗算すると乗算結果の最大値、最小値は以下のようになります。
| 乗算のパターン | 10進数表現(整数表現) | 2の補数表現 | |
| 最大値 |
(−128)*(−128) |
16384 | 0100 0000 0000 0000 |
| 最小値 |
−128*127 |
−16256 | 1100 0000 1000 0000 |
したがって、乗算結果を示すのに16ビットのビット幅が必要になります。
上記のように通常の乗算では、乗算後にカバーする値の範囲が大きくなり、乗算を繰り返すとビット幅が爆発してしまいます。
ここで、扱う数を −1から1の範囲の小数を用いると、乗算結果も −1から1の範囲の小数の同じ範囲になります。したがって、この範囲の数を扱えば、乗算を繰り返しても 扱う値の範囲は−1から1の範囲となり処理に便利です。
信号処理の世界では、上記理由より扱う数を −1から1の範囲で表す方法が良く用いられています。
8ビットの2の補数を用いて、−1から1の範囲を表すには以下のように小数点を用いればよいことになります。
このような表記を<8,0,t>と示すことにします。
意味としては、全体は8ビット、整数を示すビットは0個、tは2の補数(Two's compliment)を意味し、MSBが符号ビットとなります。
| <8,0,t> | 2の補数表現 | 10進数表現 | ||||||||
| 最大値 | 0 | . | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.9921875 |
| 最小値 | 1 | . | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1.0 |
| 符号ビット | 小数点 |
小数部 |
||||||||
| 乗算のパターン | 10進数表現(整数表現) | 2の補数表現 | |
| 最大値 |
(-1.0)*(-1.0) |
1.0であるが、1.0は表現できないので、0.9921875にクリップする | 0111 1111 |
| 最小値 |
-1.0*0.9921875 |
−0.9921875 | 10000001 |
ここで、乗算の結果1.0が生じる可能性があるが、1.0は表現できないので、正の最大値0.9921875に変更している。このような処理をCLIP(植木の端を切ってそろえること)という。
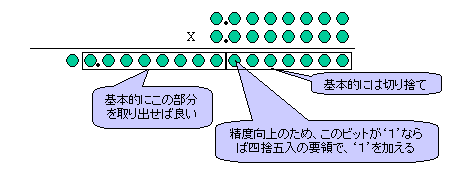
以下の図に示すように、8ビットと8ビットの乗算では16ビットの答えがいやおうなしにでることになります。今回は小数点の位置が図のようになるので、下位7ビットを切り捨てて下図の示す部分を基本的には出力することになります。
ただし、切り捨てでは精度が悪くなるので、今回は四捨五入を行います。具体的には切り捨てるビット列のMSBが’1’であれば、取り出す部分に’1’を加える処理を行います。このような処理をROUND(丸め処理)という。

| ライブラリ宣言 | library IEEE; use IEEE.STD_LOGIC_1164.all; use IEEE.STD_LOGIC_ARITH.all; |
今回は入力信号として、2の補数表現を用いた正・負混合の信号を用いるので、P63コラム4の算術演算用パー-ケージで説明されているように、std_logic_arithを用いる。 |
| エンティティ宣言 | entity MULT is port(in1 : in std_logic_vector(7 downto 0); in2 : in std_logic_vector(7 downto 0); outp : out std_logic_vector(7 downto 0)); end MULT; |
データ入力:in1, in2(8ビット) データ出力:outp(8ビット) 当然ながら、小数点はない! |
| アーキテクチャ宣言 | architecture RTL of MULT is begin |
|
| -- SIGNED CLIP ROUND MULTIPLIER -- in1 <8,0,t> -- in2 <8,0,t> -- outp <8,0,t> MULT : process(in1,in2) variable var_outp : std_logic_vector(7 downto 0); -- <8,0,t> variable var_tprod : std_logic_vector(15 downto 0); -- <16,1,t> variable var_vtrun : std_logic_vector(8 downto 0); -- <9,1,t> variable var_rndbit : std_logic; -- <1,1,u> variable var_vext : std_logic_vector(9 downto 0); -- <10,2,t> variable var_vext_1 : std_logic_vector(9 downto 0); -- <10,2,t> variable var_tinc : std_logic_vector(9 downto 0); -- <10,2,t> variable var_vrnd : std_logic_vector(9 downto 0); -- <10,2,t> variable var_vovflo : std_logic_vector(7 downto 0); -- <8,0,t> begin |
多数のVARIABLEの宣言 | |
| var_tprod := signed(in1) *
signed(in2); var_vtrun := var_tprod(15 downto 7); |
基本的な掛け算 上位の9ビット(切り捨てないビット)をとる。 |
|
| -- ROUND var_rndbit := '0'; if (var_tprod(6) = '1') then var_rndbit := '1'; end if; var_vext := var_vtrun(8) & var_vtrun; var_vext_1 := var_vtrun(8) & var_vtrun; var_tinc := signed(var_vext_1) + '1'; if (var_rndbit = '1') then var_vrnd := var_tinc; else var_vrnd := var_vext; end if; |
ROUND処理 | |
| -- CLIP (IF OVERFLOW then take
MAXVALUE) -- (IF UNDERFLOW then take MINVALUE) var_vovflo := var_vrnd(7 downto 0); if (var_vrnd(9 downto 7) /= (var_vrnd(9)&var_vrnd(9)&var_vrnd(9))) then var_vovflo := (7=>var_vrnd(9),others=>(not var_vrnd(9))); end if; |
クリップ処理 | |
| -- generate output var_outp := var_vovflo; outp <= var_outp; end process MULT; end RTL; |
出力生成 |
| ライブラリ宣言 | library STD, IEEE; use STD.TEXTIO.all; use IEEE.std_logic_1164.all; use IEEE.std_logic_textio.all; use IEEE.std_logic_arith.all; |
教科書P85にTEXTIOパッケージの説明がある。
今回、テスト入力として他のテキストファイルに書かれた値を用いるので、ライブラリSTDを指定し、パッケージTEXTIOを呼び出している。 |
| エンティティ宣言 | entity TESTBENCH_MULT is end TESTBENCH_MULT; |
テストベンチであるので、中味は空である。 |
| アーキテクチャ宣言 | architecture SIM_DATA of
TESTBENCH_MULT is component MULT port(in1 : in std_logic_vector(7 downto 0); in2 : in std_logic_vector(7 downto 0); outp : out std_logic_vector(7 downto 0)); end component; signal FMINPUT : std_logic_vector(7 downto 0); -- <8,0,t> signal MULTOUT : std_logic_vector(7 downto 0); -- <8,0,t> signal FMINPUT_I : integer; signal FMINPUT_R : real; signal FMINPUT_R2 : real; signal MULTOUT_I : integer; signal MULTOUT_R : real; signal MULTOUT_R2 : real; begin |
今回テストされるMULT回路(乗算器)をコンポーネント(部品)宣言している。
integer, realの信号はsciroccoで小数を表示するための信号 |
| -- DUT U1: MULT port map (FMINPUT, FMINPUT, MULTOUT); |
テストされる回路MULTを置いている。
in1, in2に同じ値を入れているので、波形の2乗すなわち、電力パワーを求めていることになる。 |
|
| -- TEST VECTOR P1: process file TEST_IN : text is in "fm.txt"; variable LINE_IN : line; variable V_FMINPUT : std_logic_vector(7 downto 0); begin readline(TEST_IN, LINE_IN); read(LINE_IN, V_FMINPUT); FMINPUT <= V_FMINPUT; wait for 10 ns; if endfile(TEST_IN) then wait; end if; end process; |
詳しくは、P85ページの説明とP87ページのリスト4.14を参考にしてください。
fm.txt の値を読み込んで、10nsすなわち、毎サイクルごとに値をFMINPUT信号に代入している。 if文は終了条件。 |
|
| FMINPUT_I <=
CONV_INTEGER(signed(FMINPUT)) ; FMINPUT_R <= real(FMINPUT_I) /128.0; FMINPUT_R2<= real(CONV_INTEGER(signed(FMINPUT))) /128.0; MULTOUT_I <= CONV_INTEGER(signed(MULTOUT)) ; MULTOUT_R <= real(MULTOUT_I) /128.0; MULTOUT_R2<= real(CONV_INTEGER(signed(MULTOUT))) /128.0; end SIM_DATA; |
小数をモニターするための信号を生成。 | |
| configuration CFG_MULT of TESTBENCH_MULT is for SIM_DATA end for; end CFG_MULT; |
VHDLではひとつのエンティティに複数のアーキテクチャを 持たせることができるので、その割り当ての宣言。 必ず最上位階層に記述する必要がある。 |
今回は、前回の実習で使用した正弦波データが<8,0,t>フォーマットと仮定する。そうすると、前回の波形は-1から1の区間を振動する正弦波となる。この正弦波の値を2乗した正弦波を今回生成する。出力も同じく、<8,0,t>フォーマットとする。実際には2乗すると
0) 作業ディレクトリに、上記3つのファイルをコピーする。
1) Sciroccoにて正常動作を確認せよ!
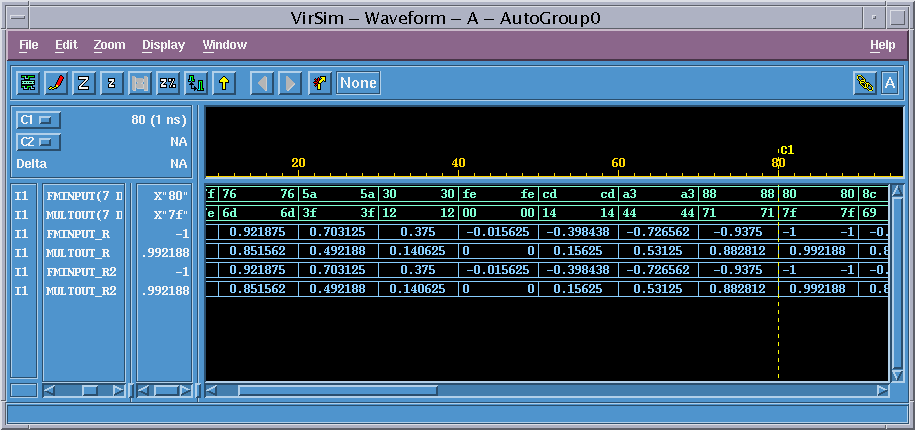
以下は波形表示、FMINPUTは正・負の波形であり、負の部分は上にシフトしているが、2乗した波形はすべて正で、正常に表示されている。
2乗することで周期が半分になる。
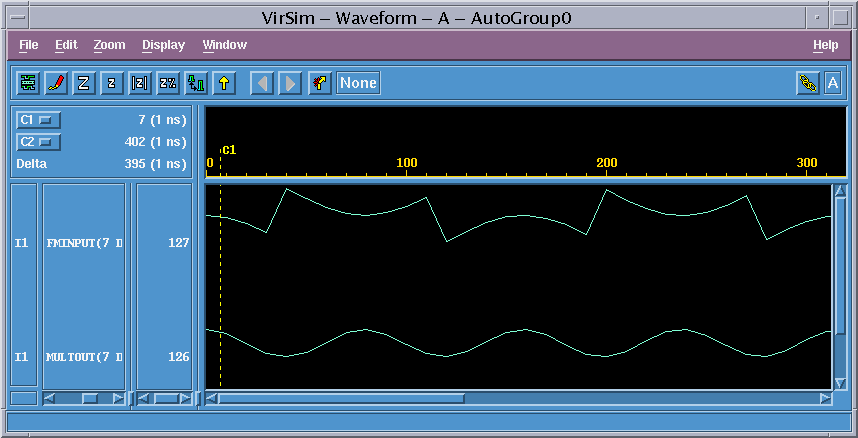
2) デザインアナライザーでmult.vhdを読み込み、入力から出力のタイミング目標を0.0nsに設定する。
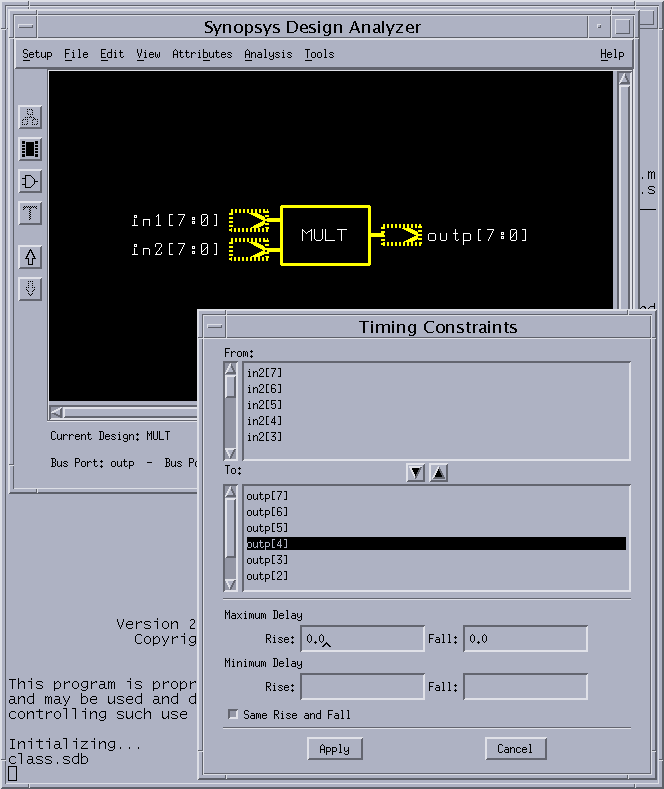
3) 回路の合成を行う。
Tool -> Design Optimization
デフォルトの設定でOK
これで、以下のような回路が合成される。
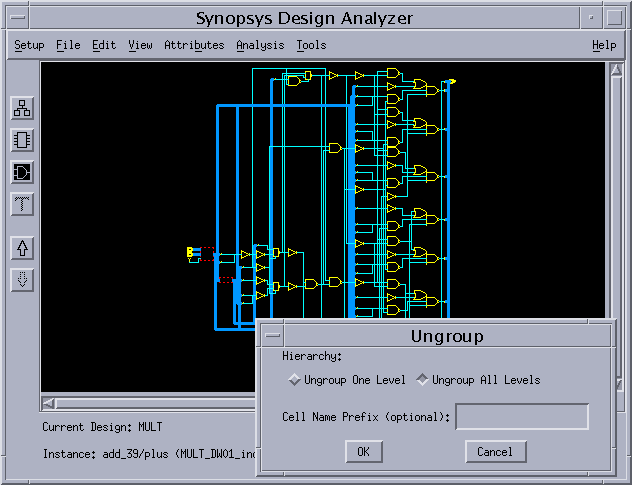
4) TOPの回路の中にあるすべてのBOX(他の回路が違うレベルにある)を展開(同一レベルに)する。
BOXをクリックして選択、
edit -> ungroup
を用いて展開する。
これをすべてのBOXに対して行う。
以下のような回路が得られる。
5)回路のクリティカルパスを表示する

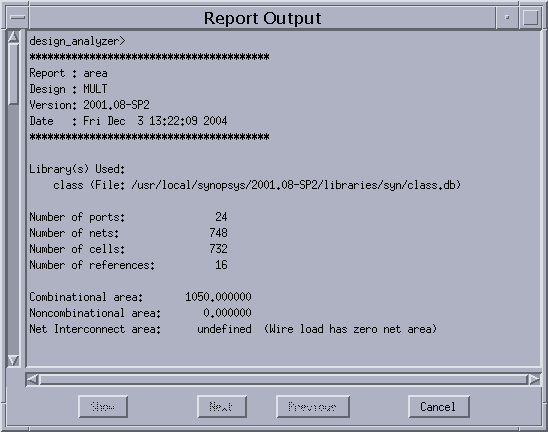
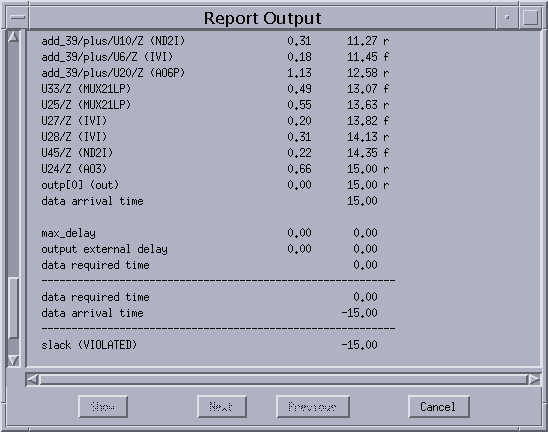
6)性能をレポートで確認する。
Analysis -> report で
area および timingをチェックしてApply
if (var_vrnd(9 downto 7) /=
(var_vrnd(9)&var_vrnd(9)&var_vrnd(9))) then
var_vovflo := (7=>var_vrnd(9),others=>(not var_vrnd(9)));
end if;
のコードを削除した場合、どのような問題点が生じるか説明し、それが生じているsciroccoシミュレーション波形を示せ。
今回の課題では1/16=0.0625のような小数点以下の数をデジタル回路で取り扱う必要があります。たとえば4ビットの2進数”0111”ですが、小数点をどこの位置に置くかで表す値が変わってきます。たとえば、”01.11”ならば10進数表現では+1.75、”0111.”ならば、10進表現では+7です。
また、4ビットの2進数ですが、それが符号無し数すなわち正または0の数を表しているか、2の補数表現で正または負の数を表しているかを区別する必要があります。”11.10”は符号無し数であれば、10進表現で+3.50となり、2の補数表現であれば、10進表現で-0.50となります。
すなわち、同じ4ビットの2進数でも、「小数点の位置」と「符号無し表現か2の補数表現か」を明確にしないとまったく異なった数に対応してしまいます。
ここではSignal Processing Workbenchで用いられている固定小数点の属性表記方法を解説し、用います。
<8,2,t>
と表記すると、その信号は
8 : 全体のビット数が8ビット
2 : 整数ビットが2ビット
t : two's complement
ということで2の補数表現、すなわち最上位ビットは符号ビットとなる
という意味です。したがって、”01101111”なる8ビットの数の属性が<8,2,t>とすると、
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 符号ビット | 整数部 |
小数部 |
|||||
ということになり、小数部は5ビットとなり、10進表現では+3.46875に対応します。
<8,2,u>
と表記すると、その信号は
8 : 全体のビット数が8ビット
2 : 整数ビットが2ビット
u : unsignedということで、符号無し数すなわち負の数を表さない
という意味です。したがって、同じ8ビットの数”01101111”の属性が<8,2,u>とすると、
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 整数部 | 小数部 | ||||||
ということになり、小数部は6ビットとなり、10進表現では+1.734375に対応します。
整数部のビット数が多いほど表現できる最大数すなわちレンジが大きくなり、小数部のビット数が多いほど表現できる最小数が小さくなり、解像度が向上します。
以下の表1に4ビットの数が<4,2,u>の属性を持つ場合と<4,1,t>の属性を持つ場合の10進表現を示します。
表1 属性による値の違い
4ビットの数 属性<4,2,u>の場合の
10進表現属性<4,1,t>の場合の
10進表現0000 +0.00 +0.00 0001 +0.25 +0.25 0010 +0.50 +0.50 0011 +0.75 +0.75 0100 +1.00 +1.00 0101 +1.25 +1.25 0110 +1.50 +1.50 0111 +1.75 +1.75 1000 +2.00 -2.00 1001 +2.25 -1.75 1010 +2.50 -1.50 1011 +2.75 -1.25 1100 +3.00 -1.00 1101 +3.25 -0.75 1110 +3.50 -0.50 1111 +3.75 -0.25
以下の表2に4ビット長の固定小数点の属性の幾つかの例と、対応する2進数、値のレンジ、解像度を示します。表2からもわかるように同じ4ビット長を用いて多様なレンジと解像度の数値を表現できます。当然のことですが、解像度を悪く大きな値にすると、より広いレンジを表すことができます。
表2 4ビット長の固定小数点の属性の幾つかの例と、対応する2進数、値のレンジ、解像度
属性 2進数表現
Sは符号ビット
Xはデータビットレンジ 解像度 整数 <1,1,u> X. 0 to 1 1 <4,4,u> XXXX. 0 to 15 1 <4,3,t> SXXX. -8 to 7 1 小数 <4,0,u> .XXXX 0.0 to 0.9375 0.0625 (1/16) <4,0,t> S.XXX -1.00 to +0.875 0.125 (1/8) その他 <4,2,u> XX.XX 0.0 to 3.75 0.25 (1/4) <4,2,t> SXX.X -4.0 to + 3.5 0.5 (1/2) <4,5,u> XXXX0. 0 to 30 2 <4,5,t> SXXX00. -32 to 28 4 <4,-1,u> .0XXXX 0.0 to 0.46875 0.03125 (1/32) <4,-1,t> S.SXXX -0.5 to +0.4375 0.0625 (1/16)
以上