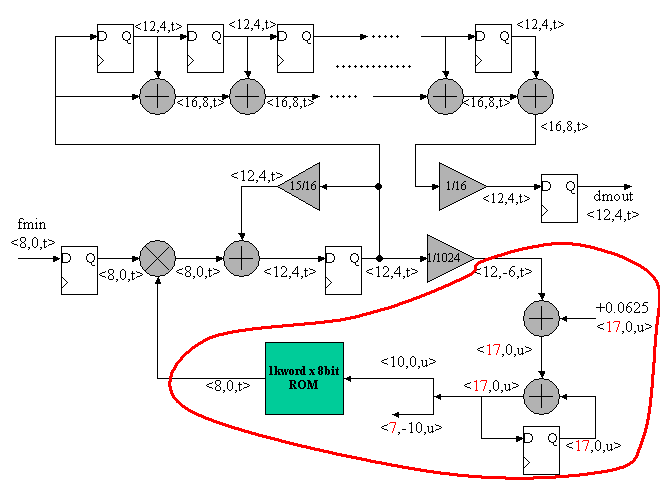
Numerical Controlled Oscillator (NCO)　数値制御型発信器

今回は入力のデジタル値を変化させることで、異なる周波数の正弦波形を出力する回路を設計する。

回路でいうと最終課題のFMレシーバーの下記赤線で囲んだ部分に相当する。

動作の概要は

  1. 右上の方から２つの入力を加算する（SUM1）
  2. その加算された入力値値をその下の加算器とFFで累積してゆく、ただし累積値は<17,0,u>で与えられるので

    　

    　 <17,0,u> １０進数表現（整数表現）
    最大値

    1 1111 1111 1111 1111

    		 0.99999237060546875
    最小値

    0 0000 0000 0000 0000

    		 0.0


    となり、累積してゆくと１．０を超えるとその部分は捨てられ０．０に戻ることになります。
    前回やった、CLIP処理はなしで使います。

    これは三角関数はちょうど２πで１周するの等価で、０から１．０でちょうど三角関数の１周期に対応します。

  3. １７ビットはあまりにも細かすぎるので、上図では上位１０ビットすなわち、１周期を１０２４点に分割し、その入力値よりCOSINEの値をテーブル（ROM）より取り出しています。

COSINE ROMのVHDL記述

リスト　cosrom.vhd

アドレス０から１０２３に対して１周期分のCOSINE値を出力する

ライブラリ宣言 library IEEE; 
use IEEE.STD_LOGIC_1164.all; 
use IEEE.STD_LOGIC_ARITH.all;		 今回は入力信号として、２の補数表現を用いた正･負混合の信号を用いるので、P63コラム４の算術演算用パー-ケージで説明されているように、std_logic_arithを用いる。
エンティティ宣言 entity COSROM is 
　port ( 
　　data : out std_logic_vector(7 downto 0); 
　　addr : in std_logic_vector(9 downto 0)
　); 
end COSROM;		 データ入力：addr（8ビット）
データ出力：data（8ビット）

　
アーキテクチャ宣言 architecture RTL of COSROM is 
begin		 　
process (addr) 
　variable iaddr : integer; 
　type rom_type is array(0 to 1023) of std_logic_vector(7 downto 0); 
　constant rom_table : rom_type := ( "01111111","01111111","01111111","01111111","01111111", "01111111","01111111","01111111","01111111","01111111",

省略

"01111111","01111111","01111111","01111111","01111111", "01111111","01111111","01111111","01111111","01111111", "01111111","01111111","01111111","01111111" ); 
begin 
　iaddr := conv_integer(unsigned(addr)); 
　data <= rom_table(iaddr); 
end process; 
end RTL;

 記述は単純で、１K＊８ビットのCOSINEのデータが多い。

回路合成すればこのような多数の値を出力する回路が合成される。

＞＞賢いツールである。

　

NCOのVHDL記述

リスト　nco.vhd

テストベンチ　test_nco.vhd

ライブラリ宣言 library IEEE; 
use IEEE.STD_LOGIC_1164.all; 
use IEEE.STD_LOGIC_ARITH.all;		 今回は入力信号として、２の補数表現を用いた正･負混合の信号を用いるので、P63コラム４の算術演算用パー-ケージで説明されているように、std_logic_arithを用いる。
エンティティ宣言 entity NCO is 
　port ( 
　　CLK : in std_logic; 
　　RESET : in std_logic; 
　　DELTA : in std_logic_vector(11 downto 0); -- <12,-6,t> 
　　OFFSET : in std_logic_vector(16 downto 0); -- <17, 0,u> 
　　COSOUT : out std_logic_vector(7 downto 0)); -- <8,0,t> 
end NCO;		 CLK：クロック入力
RESET：’１’でFFをリセット

DELTA：加算の１入力で０中心の正･負の小さな値を入力

OFFSET：加算のもう１入力で、正の大きめの値を入力

COSOUT：正弦波出力
アーキテクチャ宣言 architecture RTL of NCO is 
　component COSROM is 
　port ( 
　DATA : out std_logic_vector(7 downto 0); 
　ADDR : in std_logic_vector(9 downto 0) ); 
　end component; 

signal sum : std_logic_vector(16 downto 0); -- <17,0,u> 
signal accm : std_logic_vector(16 downto 0); -- <17,0,u> 
signal accm_d : std_logic_vector(16 downto 0); -- <17,0,u> 
signal addr : std_logic_vector(9 downto 0); -- <10,0,u> 
signal data : std_logic_vector(7 downto 0); -- <8,0,t> 

begin		 　
-- INPUT ADDER 
INPUT_SUM: process(OFFSET,DELTA) 
　variable var_vext : std_logic_vector(16 downto 0); -- <17,-1,t> 
　variable var_tsum : std_logic_vector(16 downto 0); -- <17,-1,t> 
begin 
　var_vext := DELTA(11)&DELTA(11)&DELTA(11)&DELTA(11)&DELTA(11)&DELTA;
　var_tsum := signed(OFFSET) + signed(var_vext); 
　sum <= var_tsum; 
end process INPUT_SUM;		 最初の加算器

２の補数と符号無し数の加算なので、どちらも２の補数にして加算している。

ビット幅、小数点の位置を合わせている。
-- ACCUMULATOR 
accm <= unsigned(sum) + unsigned(accm_d); 

ACCM_DFF: process(CLK, RESET) begin 
　if(RESET = '1') then 
　　accm_d <= "00000000000000000"; 
　elsif(CLK'event and CLK = '1') then 
　　accm_d <= accm; 
　end if; 
end process ACCM_DFF;		 加算器

リセット付フリップフロップ

初期値の値が累積するので、初期値を’０’にリセットする機能が必要。
-- COSINE ROM 
addr <= accm(16 downto 7); 
U1: COSROM port map (data, addr);		 入力アドレスを１０ビット可

COSINEROM
-- OUTPUT FF 
OUT_FF: process(CLK) begin 
　if(CLK'event and CLK='1') then 
　　COSOUT <= data; 
　end if; 
end process OUT_FF;		 上図の回路にはないが、合成のタイミング制約をしやすくするために、出力にFFを置いている。
end RTL; 出力生成

　

テストベンチのVHDL記述

ライブラリ宣言 library IEEE; 
use IEEE.STD_LOGIC_1164.all; 
use IEEE.STD_LOGIC_ARITH.all;		 　
エンティティ宣言 entity TESTBENCH_NCO is 
end TESTBENCH_NCO;		 テストベンチであるので、中味は空である。
アーキテクチャ宣言 architecture SIM_DATA of TESTBENCH_NCO is 

component NCO is port ( 
　CLK : in std_logic; 
　RESET : in std_logic; 
　DELTA : in std_logic_vector(11 downto 0); -- <12,-6,t> 
　OFFSET : in std_logic_vector(16 downto 0); -- <17, 0,u> 
　COSOUT : out std_logic_vector(7 downto 0) ); -- <8,0,t> 
end component; 

signal OFFSET : std_logic_vector(16 downto 0); 
signal DELTA : std_logic_vector(11 downto 0); 
signal COSOUT : std_logic_vector(7 downto 0); 
signal CLK : std_logic := '1'; 
signal RESET : std_logic := '1'; 

signal COSOUT_REAL : real; 
signal OFFSET_REAL : real; 
signal DELTA_REAL : real; 

signal COSOUT_OFFSET : std_logic_vector(7 downto 0); 

begin

 今回テストされるNCO回路をコンポーネント（部品）宣言している。

realの信号はsciroccoで小数を表示するための信号

COSOUT_OFFSETは正･負の２の補数を波形表示するために、すべて正の領域にずらした信号。（オフセットバイナリ-表現）
-- CLOCK GENERATION 
CLK <= not CLK after 5 ns; 

-- RESET release 
P1: process begin 
　RESET <= '1'; wait for 20 ns; 
　RESET <= '0'; wait; 
end process;

 クロック信号、初期リセット信号の生成
-- DATA VALUE 
P2: process begin 
　OFFSET <= "00010000000000000"; -- 1/16 
　DELTA <= "011111111111"; -- +0.0156 (+1/64) 
　wait for 1000 ns; 
　DELTA <= "100000000000"; -- -0.0156 (-1/64) 
　wait for 1000 ns; 
　DELTA <= "011111111111"; -- +0.0156 (+1/64) 
　wait; 
end process; 		OFFSET値は1/16で固定、

DELTAを1/64､-1/61、1/64と1000 ns ごとに変化させている。
-- DUT 
U1: NCO port map (CLK, RESET, DELTA, OFFSET, COSOUT);		 NCOが置かれている。
-- MONITOR 
COSOUT_REAL <= real(CONV_INTEGER(signed(COSOUT))) /128.0;
OFFSET_REAL <= real(CONV_INTEGER(signed(OFFSET))) /2.0**17;
DELTA_REAL <= real(CONV_INTEGER(signed(DELTA))) /2.0**17;

COSOUT_OFFSET <= (not COSOUT(7)) & COSOUT(6 downto 0); 

end SIM_DATA;

 モニター用信号生成

COSOUT_OFFSETは２の補数表現のMSBを反転している。これで、波形が正の領域に移動する。
configuration CFG_NCO of TESTBENCH_NCO is 
　for SIM_DATA 
　end for; 
end CFG_NCO;		 　

　

実習６　NCOの動作シミュレーション(1)

今回は、前回の実習で使用した正弦波データが<8,0,t>フォーマットと仮定する。そうすると、前回の波形は-1から1の区間を振動する正弦波となる。この正弦波の値を２乗した正弦波を今回生成する。出力も同じく、<8,0,t>フォーマットとする。実際には２乗すると

リスト　cosrom.vhd

リスト　nco.vhd

テストベンチ　test_nco.vhd

０）　作業ディレクトリに、上記３つのファイルをコピーする。

１）　Sciroccoにて正常動作を確認せよ！

実習５（２）

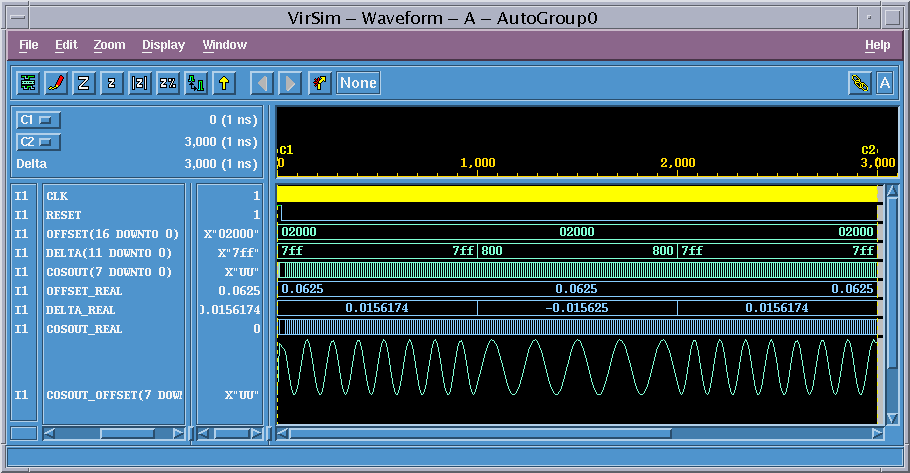
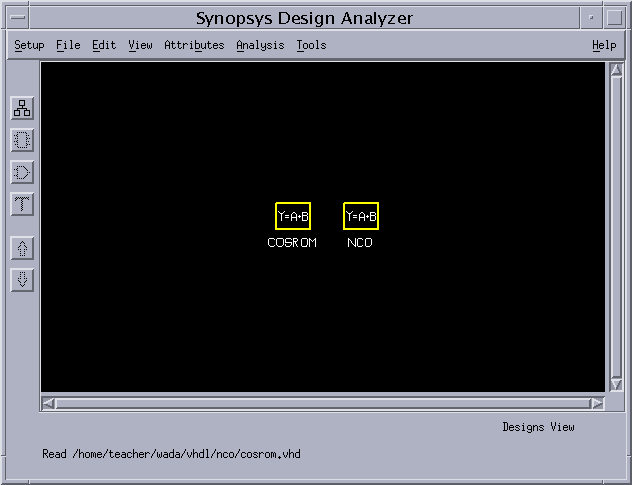
２）　今回の設計は２つのファイルから構成されているので、デザインアナライザーでnco.vhd、cosrom.vhdの両方を読み込む。

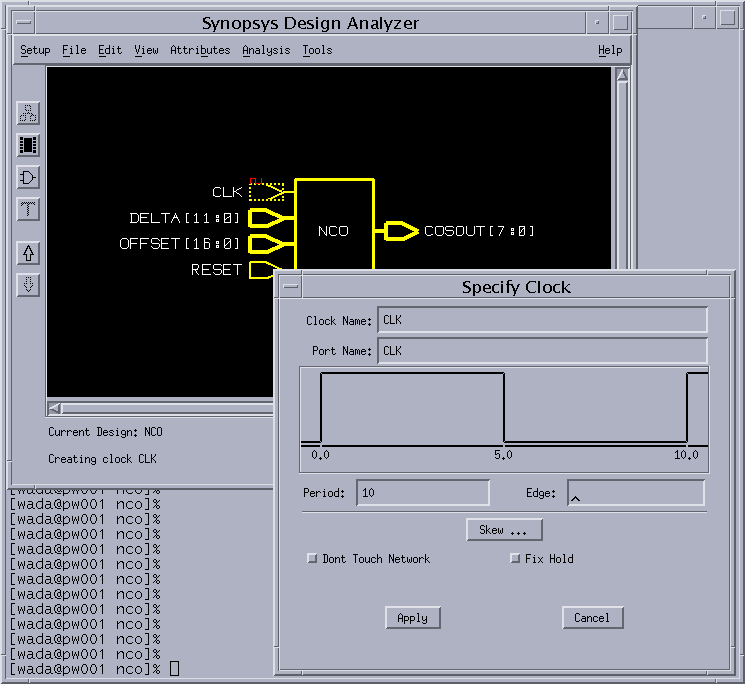
３）　NCOのクロックピンを選択して、サイクルタイムのターゲットを　10 ns に設定する。

４）　NCOを選択して、回路の合成を行う。

Tool -> Design Optimization

デフォルトの設定でOK

これで、以下のような回路が合成される。

５）　TOPの回路の中にあるすべてのBOX（他の回路が違うレベルにある）を展開（同一レベルに）する。

BOXをクリックして選択、

edit -> ungroup

を用いて展開する。

これをすべてのBOXに対して行う。

以下のような回路が得られる。

６）回路のクリティカルパスを表示する

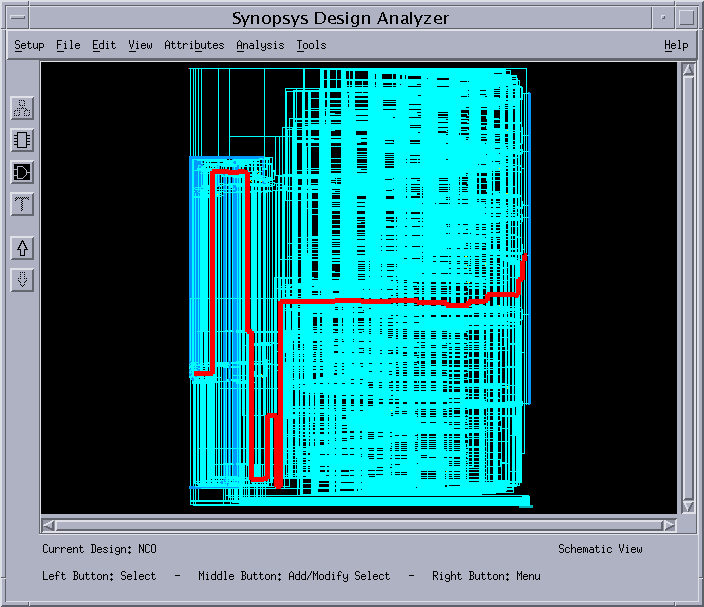
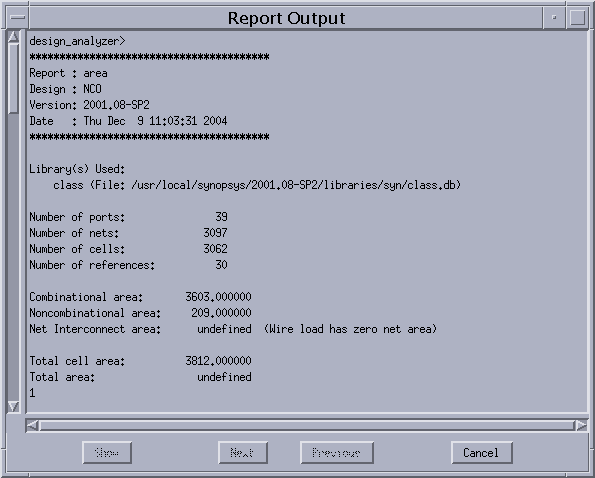
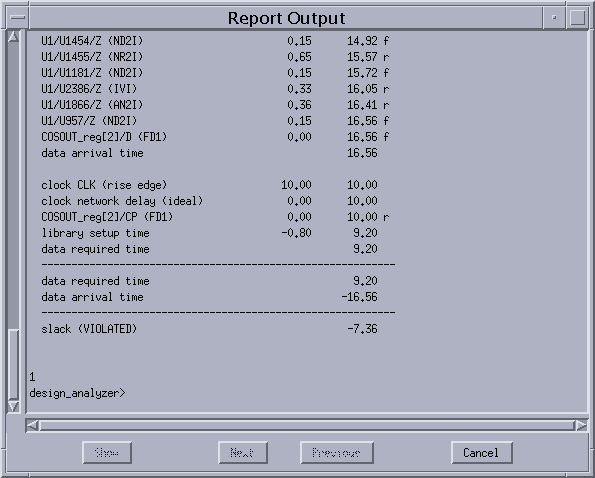
７）性能をレポートで確認する。

Analysis -> report　で

area および timingをチェックしてApply

　

実習６（３）・宿題６

固定小数点フォーマットの補足

今回の課題では1/16＝0.0625のような小数点以下の数をデジタル回路で取り扱う必要があります。たとえば４ビットの２進数”０１１１”ですが、小数点をどこの位置に置くかで表す値が変わってきます。たとえば、”０１．１１”ならば１０進数表現では＋１．７５、”０１１１．”ならば、１０進表現では＋７です。

また、４ビットの２進数ですが、それが符号無し数すなわち正または０の数を表しているか、２の補数表現で正または負の数を表しているかを区別する必要があります。”１１．１０”は符号無し数であれば、１０進表現で+3.50となり、２の補数表現であれば、１０進表現で-0.50となります。

すなわち、同じ４ビットの２進数でも、「小数点の位置」と「符号無し表現か２の補数表現か」を明確にしないとまったく異なった数に対応してしまいます。

ここではSignal Processing Workbenchで用いられている固定小数点の属性表記方法を解説し、用います。

<8,2,t>

と表記すると、その信号は

８　：　全体のビット数が８ビット
２　：　整数ビットが２ビット
ｔ　：　two's complement ということで２の補数表現、すなわち最上位ビットは符号ビットとなる

という意味です。したがって、”０１１０１１１１”なる８ビットの数の属性が<8,2,t>とすると、

0 1 1 0 1 1 1 1
符号ビット 整数部

小数部

ということになり、小数部は５ビットとなり、１０進表現では＋３．４６８７５に対応します。

<8,2,u>

と表記すると、その信号は

８　：　全体のビット数が８ビット
２　：　整数ビットが２ビット
u　：　unsignedということで、符号無し数すなわち負の数を表さない

という意味です。したがって、同じ８ビットの数”０１１０１１１１”の属性が<8,2,u>とすると、

0 1 1 0 1 1 1 1
整数部 小数部

ということになり、小数部は６ビットとなり、１０進表現では＋１．７３４３７５に対応します。

整数部のビット数が多いほど表現できる最大数すなわちレンジが大きくなり、小数部のビット数が多いほど表現できる最小数が小さくなり、解像度が向上します。

以下の表１に４ビットの数が<4,2,u>の属性を持つ場合と<4,1,t>の属性を持つ場合の１０進表現を示します。

表１　属性による値の違い

4ビットの数 属性<4,2,u>の場合の
１０進表現		 属性<4,1,ｔ>の場合の
１０進表現
0000 +0.00 +0.00
0001 +0.25 +0.25
0010 +0.50 +0.50
0011 +0.75 +0.75
0100 +1.00 +1.00
0101 +1.25 +1.25
0110 +1.50 +1.50
0111 +1.75 +1.75
1000 +2.00 -2.00
1001 +2.25 -1.75
1010 +2.50 -1.50
1011 +2.75 -1.25
1100 +3.00 -1.00
1101 +3.25 -0.75
1110 +3.50 -0.50
1111 +3.75 -0.25

以下の表２に４ビット長の固定小数点の属性の幾つかの例と、対応する２進数、値のレンジ、解像度を示します。表２からもわかるように同じ４ビット長を用いて多様なレンジと解像度の数値を表現できます。当然のことですが、解像度を悪く大きな値にすると、より広いレンジを表すことができます。

表２　４ビット長の固定小数点の属性の幾つかの例と、対応する２進数、値のレンジ、解像度

　 属性 ２進数表現
Sは符号ビット
Xはデータビット		 レンジ 解像度
整数 <1,1,u> X. 0 to 1 1
<4,4,u> XXXX. 0 to 15 1
<4,3,t> SXXX. -8 to 7 1
小数 <4,0,u> .XXXX 0.0 to 0.9375 0.0625 (1/16)
<4,0,t> S.XXX -1.00 to +0.875 0.125 (1/8)
その他 <4,2,u> XX.XX 0.0 to 3.75 0.25 (1/4)
<4,2,t> SXX.X -4.0 to + 3.5 0.5 (1/2)
<4,5,u> XXXX0. 0 to 30 2
<4,5,t> SXXX00. -32 to 28 4
<4,-1,u> .0XXXX 0.0 to 0.46875 0.03125 (1/32)
<4,-1,t> S.SXXX -0.5 to +0.4375 0.0625 (1/16)

以上