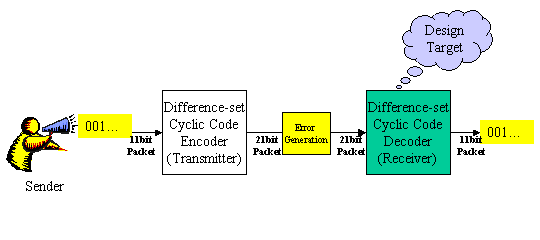
図1 送受信システム図
琉球大学工学部情報工学科 和田 知久
今回はテレビの文字多重放送に用いられているエラー訂正方式である差集合巡回符号を用いたエラー訂正回路の設計を行います。とはいえ、学生対象のコンテストですので、小さめのデジタル回路を設計することを念頭に、符号長を実際に使用されている長さよりかなり短くし、取り扱いやすい大きさとします。また、いくつの設計オプションを設定し、各個人やチームによって色々な工夫ができるように、実現方法には自由度をある程度与えています。
要求されている設計内容はHDL(VHDLもしくはVerilogHDL)による設計と論理合成です。特にシノプシス社の合成ツールを使用する必要はなく、FPGA等の合成ツールでも参加できます。HDL設計に興味のある学生はどしどし参加してください。また、余裕のある方はFPGA等で実装すれば、努力を認めて高い評価が得られると思います。FPGA等での実装もぜひトライしてみてください。

図1 送受信システム図
図1に今回設計するデジタルデータの送受信システムのブロック図を示します。システムは大きく分けて、送信機(Transmitter)と受信機(Receiver)に分かれますが、今回の設計課題は受信機(Receiver)です。
送信者はビット列を出力します。送信機はシリアルに入力されるビット列11ビットに対して差集合巡回符号の符号化処理(Encode)を行い、11ビットの入力にエラー訂正用のビット列10ビットを付加して21ビットの符号とします。この21ビットが伝送されるわけですが、伝送中にビットエラーが発生します。図1ではError Generationブロックがエラーを発生させます。
受信機ではこのエラーを含んだ21ビットの符号を受け取り、エラー訂正処理を行います。エラー訂正処理には有名なところではリード・ソロモン方式などがありますが、処理が複雑で学生対象のコンテストには不向きです。しかしながら、差集合巡回符号方式では、多数決回路でエラー訂正をやることができ、回路的には非常にシンプルです。
今回の課題では差集合巡回符号の知識がなくても設計できるように、以下の仕様書で工夫をしています。設計すべきことは比較的単純ですので、デジタル設計の知識のある学生は自信を持って、課題に取り組んでください。
デジタルデータの伝送時のエラーの発生の有無をチェックするのにパリティチェックという方式がよく用いられます。以下の表に、8ビットのデータに1ビットのパリティビットを付加した例を種類示します。8ビットデータの中の’1’の個数が偶数であれば、パリティビットは’0’であり、’1’の個数が奇数個であれば、パリティビットは’1’となります。したがって、パリティビット生成回路は非常に簡単であり、表1のParity発生回路のように他入力のEXOR(排他的論理輪)となります。
|
8ビットのデータ |
パリティビット | Parity発生回路 | |||||||
| D7 | D6 | D5 | D4 | D3 | D2 | D1 | D0 | Parity | 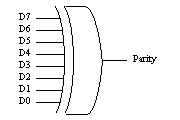 |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
表1 8ビットパリティの例とパリティ発生回路
したがって、Parityビットを付加した9ビット幅のデータを送信し、受信側で{D7, D6, D5, D4, D3, D2, D1, D0, Parity}のEXORを取り、その出力が’1’であれば、どこかにエラーが発生したことが検知でき、EXORの出力が’0’であればエラーが発生しなかったと判断できます。但し、2ビットのエラーは検知できませんし、送信した9ビットのうちどのビットがエラーで反転したかを知ることができません。
差集合巡回符号を文献等で調査するとガロア体の多項式等をもちいたややこしい理論が説明されています。しかし、ここでは符号理論に詳しくない方、むしろデジタル回路設計者のような他分野の方に理解しやすいように、差集合巡回符号を用いたエラー訂正方法を紹介します。
今回設計するシステムでは先にも説明したように、11ビットの情報ビットに対して10ビットのエラー訂正用のビットを付加し、21ビットのデータを送信します。この21ビットには以下に示すような面白い特性があります。
表2に、11ビットの情報ビットとして{1,1,1,1,1,1,1,1,1,1,1}なるすべて’1’からなる情報を送る場合の例を示します。エラー訂正用の10ビットは表2のようになります。この生成方法は後ほど説明します。
|
エラー訂正用(10ビット) |
情報ビット(11ビット) |
||||||||||||||||||||
| 情報ビット(11ビット) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||
| 送信ビット(21ビット) | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
表2 情報ビット(11ビット)と送信ビット(21ビット)の例
この21ビットの送信ビットに対して以下の表3に示すような5種類A1〜A5のパリティチェックを考えます。
| ビットの位置番号 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 送信ビット(SB) | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| パリティチェックA1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||
| パリティチェックA2 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||
| パリティチェックA3 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||
| パリティチェックA4 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||
| パリティチェックA5 | 1 | 1 | 1 | 1 | 1 |
表3 情報ビット(11ビット)と送信ビット(21ビット)の例
パリティチェックA1ではビット番号で9, 12, 13, 18, 20にところに1があります。この5つの位置に対応する送信ビットSB(9), SB(12), SB(13), SB(18), SB(20)のEXORを取ると、’0’となります。同様にパリティチェックA2〜A5でもすべて’0’となります。まとめると、以下のようになります。
| パリティチェックA1 | A1 = SB(9) exor SB(12) exor SB(13) exor SB(18) exor SB(20) = 0 |
| パリティチェックA2 | A2 = SB(1) exor SB(11) exor SB(14) exor SB(15) exor SB(20) = 0 |
| パリティチェックA3 | A3 = SB(4) exor SB(6) exor SB(16) exor SB(19) exor SB(20) = 0 |
| パリティチェックA4 | A4 = SB(0) exor SB(5) exor SB(7) exor SB(17) exor SB(20) = 0 |
| パリティチェックA5 | A5 = SB(2) exor SB(3) exor SB(8) exor SB(10) exor SB(20) = 0 |
表4 5種類のパリティチェック
ここで送信ビットの20ビット目SB(20)がエラーで反転した場合を考えます。SB(20)は5種類のパリティチェック式にすべて含まれています。したがって、5つのパリティチェック式A1からA5はすべて’1’となります。
また、送信ビットの20ビット目以外で1箇所のエラーが発生した場合を考えます。表3を見てわかるように、送信ビットの20ビット目以外のビットは5種類のパリティチェック式のどれかに1回のみ使用されます。したがって、A1からA5のうちどれか1つが’1’となります。
したがって、上記パリティチェック式を計算し、その多数が’1’となるとSB(20)にエラーが発生していることが検知され、SB(20)のビットを反転することでエラーの訂正を行うことができます。
上記例ではSB(20)のエラー訂正の方法を説明しました。このセクションでは他のビット番号の場所のエラー訂正の方法を説明します。
| ビットの位置番号 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 送信ビット(SB) | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| パリティチェックA1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||
| パリティチェックA2 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||
| パリティチェックA3 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||
| パリティチェックA4 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||
| パリティチェックA5 | 1 | 1 | 1 | 1 | 1 |
表5 SB(19)を訂正するパリティチェック
表5にSB(19)を訂正するためのパリティチェックの方法を示します。これは単に表3のSB(20)を訂正するパリティチェックを示す’1’を全体に左に1ビットシフトしたものとなっています。そして、一番左端であふれた’1’を右端に巡回させています。このようにシフトしたパリティチェックを用いればSB(19)ビットを同様に訂正することができます。
同様にパリティチェック式をシフトをすることで、他のビット位置のエラーを訂正することが可能となります。
これまで複雑な多項式を用いず例題を用いて説明してきました。しかしながら、送信回路や受信回路のシンドローム計算回路では多項式を割り算し余りを求める回路が必要になりますので、多項式を用いた説明を以下行います。
11ビットの情報ビットを{u0, u1, u2, u3, u4, u5, u6, u7, u8, u9, u10}とし、以下の多項式U(x)で表します。
![]() ---- (1)
---- (1)
そうすると、21ビットの送信ビットは以下のような多項式SB(x)で示すことができます。
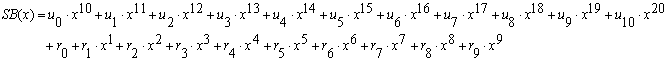 ----(2)
----(2)
これを表で示すと、以下の表6のようになる。
|
エラー訂正用(10ビット) |
情報ビット(11ビット) |
||||||||||||||||||||
| 情報ビット(11ビット) | u0 | u1 | u2 | u3 | u4 | u5 | u6 | u7 | u8 | u9 | u10 | ||||||||||
| 送信ビット(21ビット) | r0 | r1 | r2 | r3 | r4 | r5 | r6 | r7 | r8 | r9 | u0 | u1 | u2 | u3 | u4 | u5 | u6 | u7 | u8 | u9 | u10 |
表6 情報ビット(11ビット)と送信ビット(21ビット)の例
すなわち、
![]() ----(3)
----(3)
を求めれば、U(x)が与えられているので、容易にSB(x)を生成することが可能となります。実はR(x)は
![]() ----(4)
----(4)
を
![]() ----(5)
----(5)
で割り算を行った余りとなります。但し、ガロア体という普通の数学ではない割り算の余りを求めることになります。
(5)式の次数は10次なので、(4)式を(5)式で割った余りは9次式以下の次数となります。ガロア体での多項式の余りを求める方法は実は単純であり、
![]() ----(6)
----(6)
を用いて、10次の項を7次以下の式への変換を繰り返し用いることで、(4)式の次数を9次以下に下げるように変換することで求めることができます。但しこのとき、係数どおしの加算や減算はEXORで代用します。すなわち、
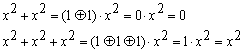 ----(7)
----(7)
のように計算します。
図2に送信機の回路図を示します。クロックに同期して、IN入力より情報ビットを u10, u9, ..., u0の順に入力します。このとき2つのスイッチはA側に接続しておきます。そうすると、OUT出力端子よりu10, u9, ..., u0がそのまま出力されると同時にr9, r8, ..., r0フリップフロップと排他的論理輪EXORで構成されるガロア体の割り算の余り計算回路で(3)式で示される係数が計算されます。
![]() ----(5)
----(5)
で割り算を行いますので、
![]() ----(6)
----(6)
なる式を用いて式の次数を下げることになります。すなわち、INからの信号は10次の係数に対応し、10次の係数が1の場合、0次、2次、4次、6次、7次の係数に’1’をEXORとることになります。回路をみるとまさに(6)式で示す計算をやっていることになります。結果的に、INに11個の値をすべて入力すると、r9, r8, ..., r0なるフリップフロップにガロア体の割り算の余りの係数が発生します。
その後にスイッチをB方向に接続すると、r9, r8, ..., r0なる係数は右方向へ順にシフトし、OUT端子から出力されます。この詳しい動作タイミングを図3に示します。
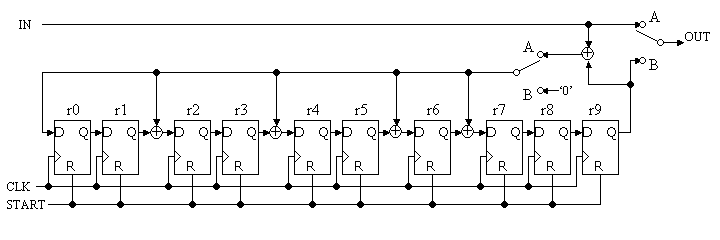
図2 送信機の回路図
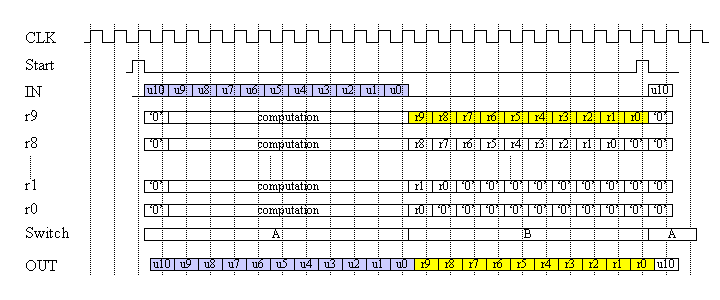
図3 送信機の動作タイミング図
図3では情報ビットの入力を示すために、Start信号を用い、Start信号によりr9, r8, ..., r0なるフリップフロップの同期リセットも行っています。Start信号は21サイクルごとに入力することにします。
表7および表8に情報ビットが(0,0,0,0,0,0,0,0,0,0,1) の場合と、(1,1,1,1,1,1,1,1,1,1,1) の場合のレジスタの値の時間的変化を示しておきます。
情報ビットが(0,0,0,0,0,0,0,0,0,0,1) の場合は、u0=1すなわち、10次の係数が1であり、
![]() ----(6)
----(6)
なる処理を1回やっていることが理解できると思います。
| Signal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| AB Switch | - | A | A | A | A | A | A | A | A | A | A | A | B | B | B | B | B | B | B | B | B | B |
| IN | - | u10 0 |
u9 0 |
u8 0 |
u7 0 |
u6 0 |
u5 0 |
u4 0 |
u3 0 |
u2 0 |
u1 0 |
u0 1 |
- | - | - | - | - | - | - | - | - | - |
| r9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||
| r8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||
| r7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | ||||||||||
| r6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | ||||||||||
| r5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||
| r4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | ||||||||||
| r3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||
| r2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | ||||||||||
| r1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||
| r0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | ||||||||||
| OUT | - | u10 0 |
u9 0 |
u8 0 |
u7 0 |
u6 0 |
u5 0 |
u4 0 |
u3 0 |
u2 0 |
u1 0 |
u0 1 |
r9 0 |
r8 0 |
r7 1 |
r6 1 |
r5 0 |
r4 1 |
r3 0 |
r2 1 |
r1 0 |
r0 1 |
表7 情報ビット=(0,0,0,0,0,0,0,0,0,0,1) を送信する場合の送信回路の動作
情報ビットが(1,1,1,1,1,1,1,1,1,1,1) の場合は、u10=1すなわち、20次の係数が1であり、
![]() ----(6)
----(6)
なる処理をサイクル1で行うことで、その後の10サイクルでシフト動作を行うことで等価的に、
![]() ----(8)
----(8)
やっていることが理解できると思います。
| Signal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| AB Switch | - | A | A | A | A | A | A | A | A | A | A | A | B | B | B | B | B | B | B | B | B | B |
| IN | - | u10 1 |
u9 1 |
u8 1 |
u7 1 |
u6 1 |
u5 1 |
u4 1 |
u3 1 |
u2 1 |
u1 1 |
u0 1 |
- | - | - | - | - | - | - | - | - | - |
| r9 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | ||||||||||
| r8 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | ||||||||||
| r7 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | ||||||||||
| r6 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | ||||||||||
| r5 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | ||||||||||
| r4 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | ||||||||||
| r3 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | ||||||||||
| r2 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | ||||||||||
| r1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | ||||||||||
| r0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | ||||||||||
| OUT | - | u10 1 |
u9 1 |
u8 1 |
u7 1 |
u6 1 |
u5 1 |
u4 1 |
u3 1 |
u2 1 |
u1 1 |
u0 1 |
r9 0 |
r8 0 |
r7 0 |
r6 1 |
r5 0 |
r4 0 |
r3 1 |
r2 1 |
r1 0 |
r0 0 |
表8 情報ビット=(1,1,1,1,1,1,1,1,1,1,1) を送信する場合の送信回路の動作
さて、いよいよ受信機の仕様を説明します。受信機では、表4で示したA1からA5のパリティチェックを行う必要があります。もちろん、表4に示したパリティチェックを行っても構いませんが、後ほどの性能改善のためにシンドロームを計算する方法を説明します。
先に説明したように、21ビットの送信信号は
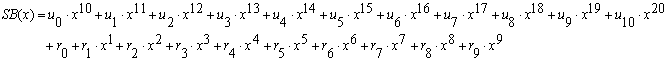 ----(2)
----(2)
のようになります。
![]() ---(9)
---(9)
R(x)はX(x)を(5)式のG(x)で割った余りであるので、SB(x)はG(x)で割り切れることになります。
今、送信信号SB(x)を送信して、RB(x)なる信号を受信したとします。送信中にエラーがなければ、RB(x)はSB(x)と同一であり、RB(x)をG(x)で割ると余りは0となります。もし送信中にエラーが発生すると、RB(x)をG(x)で割った余りは0ではなく、エラーの発生を検知することができます。
今、このRB(x)をG(x)で割った余りをS(x)シンドロームとすると、S(x)は以下のような9次の多項式となります。
![]() ---(10)
---(10)
実は前に説明した5つのパリティチェック式は(10)式のシンドローム係数により簡単に計算することができます。この方法を以下の表9に示します。
| パリティチェックA1 | A1 = s9 = SB(9) exor SB(12) exor SB(13) exor SB(18) exor SB(20) |
| パリティチェックA2 | A2 = s1 = SB(1) exor SB(11) exor SB(14) exor SB(15) exor SB(20) |
| パリティチェックA3 | A3 = s4 exor s6 =SB(4) exor SB(6) exor SB(16) exor SB(19) exor SB(20) |
| パリティチェックA4 | A4 = s0 exor s5 exor s7 = SB(0) exor SB(5) exor SB(7) exor SB(17) exor SB(20) |
| パリティチェックA5 | A5 = s2 exor s3 exor s8 = SB(2) exor SB(3) exor SB(8) exor SB(10) exor SB(20) |
表9 シンドロームによる5種類のパリティチェックの導出
シンドロームはRB(x)をG(x)で割った余りなので、送信機で用いた回路(正式名:リニア・フィードバック・シフトレジスタ)と同じ回路を用いることで、S(x)をすなわち、係数s0, s1, ... , s9を求めることができます。
以下に、リニアフィードバックレジスタにより余りを計算し、すなわちシンドロームを計算し、A1からA5のパリティチッケイを行い、3つ以上のパリティチェックが1になった場合にエラーを発見する(ERROR_FOUND信号を1とする)方式を用いた、受信機の回路例を示します。
21ビットの受信信号の入力が終了し、シンドローム値s0, s1, ... , s9が計算されると、最上位の受信信号ビットRB(20)用のパリティが計算され、多数決回路により、エラーが発生したかどうかが計算されます。そして、エラーが発生した場合、21ビットシフトレジスタの右側にEXORによりエラーが訂正されます。その後に、EN信号を’0’とし、ANDゲートの出力を’0’に固定して、シンドロームビットを同じ回路で1ビットシフトすると、RB(19)用のパリティが計算され、またRB(19)が21ビットシフトレジスタより出力され、RB(19)にのエラー訂正をすることができます。この処理を繰り返すことで、21ビットの受信信号すべてにエラー訂正処理を行うことができます。
図中、CLK信号の引き回しは省略しています。
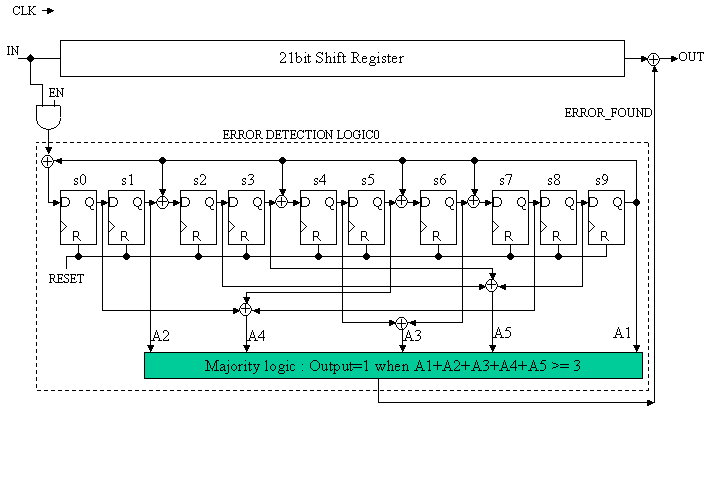
図4 初心者用受信回路の一例
今回設計するシステムの構成を図5に示します。システムは大きくわけて、TRANSMITTER(送信機)とRECEIVER(受信機)、そして受信機でエラー訂正された受信機の出力(RBEC)のエラーの数をカウントするためのERRORCNT(エラーカウント機)からなり、設計してもらうのは、RECEIVERとERRORCNTです。実際に回路合成を行い、回路規模やスピードを求めるのはRECEIVERだけとなり、ERRORCNTは自分で設計したRECEIVERのエラー訂正の能力の評価に使用します。
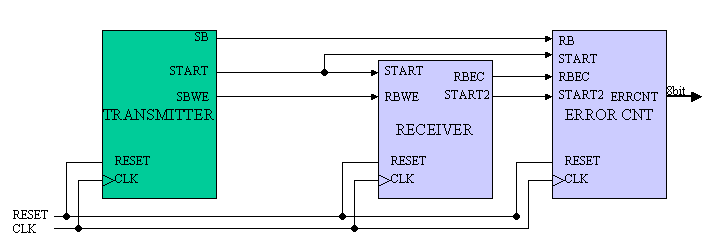
図5 システム構成図
(TRANSMITTER:送信機の説明)
TRANSMITTERは送信機であり、11ビットの情報ビット列U(x)を生成し、10ビットのエラー訂正用ビット列R(x)を付加して、21ビットの送信データSB(x)を生成します。
送信機は21ビットの送信データの前に同じく21ビットの決まったシーケンス(同期信号と呼ぶ)を付加します。この連続した値はMSB→LSBの順に示して’001101011110111000000’とします。送信機ではMSBから順に出力されます。
さらに送信機は同期信号が付加され42ビット長となった信号に適当なエラーを発生させ、その出力をSBWE端子に出力します。SBWEには連続的に1か0の信号がクロックCLKに同期して出力されます。説明したように、42サイクルで42ビットを送信し、この42サイクルごとに1つの11ビットの情報ビット列を送信することになります。この42ビットの送信は連続的に発生し、常に42サイクルごとに11ビットの情報ビット列が送信されることになります。
START信号は42サイクル中1サイクル期間のみ、1を出力し、21ビットの送信データの先頭位置を示します。
SBはRECEIVERによるエラー訂正がうまくできているかを調べる目的に用意された信号であり、SBWE端子の出力に対応したエラーが含まれてない正しい信号を出力します。実際の通信システムではこのような信号はありませんが、ここではエラー訂正の評価のために特別に用意します。
(RECEIVER:受信機の説明)
RECEIVERは受信機であり、クロックに同期して、TRANSMITTERからの送信信号SBWEを受け取ります。42サイクルごとにそこに含まれる21ビットの送信データを用いて、エラー訂正された11ビットの情報ビット列をRBEC端子に出力します。21ビットの送信データの先頭位置はSTART信号を用いて知ることができます。しかしながら、上級者用の課題ではRECEIVERはSTART信号を使用せず、RBWEに含まれる21ビットの決まった同期信号を用いてSTART信号を内部で発生させます。
ただし、21ビットの同期信号にもエラーが発生しているので、注意が必要です。
(ERRORCNT:エラーカウント機)
ERRORCNTは受信機の評価用のブロックであり、回路合成等は行いません。TRANSMITTERよりSTART信号とエラーのない送信信号SBを受け取ります。したがって、いつも正しい情報ビットを知ることができます。また、ERRORCNTはRECEIVERよりエラー訂正された情報ビットをRBEC端子より受け取ります。ERRORCNTは正しい情報ビットとエラー訂正された情報ビットを比較を行い、内部に持つ8ビットのレジスタに累積のエラーの発生回数を記憶し、外部へERRCNT端子を通して出力します。8ビットですので、255までのエラーをカウントできることにします。
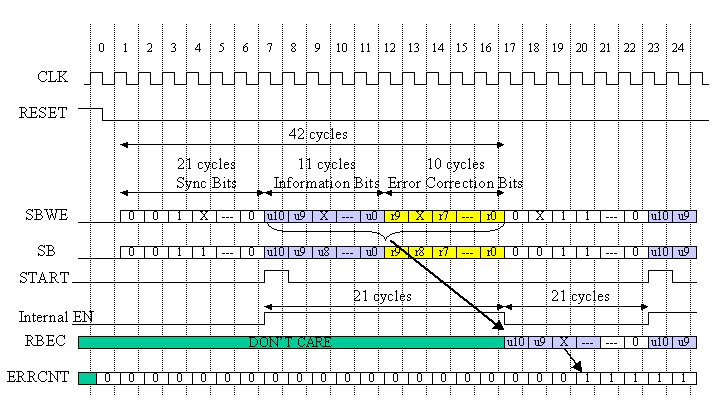
図6 システム動作タイミング図
図6に動作タイミング図を示します。RESET信号の解除の後、TRANSMITTERはSBWE(Sent Bits With Error)信号、SB(Sent Bits without error)信号、START信号を出力します。42サイクルがひとつの単位となっており、最初の21サイクルは決まった値が送信され、その後の11サイクルで情報ビットが、その後の10サイクルでエラー訂正用ビットが送信されます。SBWEはエラー付の信号であり、ある確率でエラーが発生します。詳しくは与えられたTRANSMITTERのVHDL記述を見てください。もちろん、最初の同期用の21サイクルの信号にもエラーが発生しますので、レベル3の上級者課題をやる方は注意が必要です。
この同期用の21ビットの値はMSB→LSBの順に示して’001101011110111000000’で、MSBを先頭に送信されます。
RECEIVERはSBWE信号を受信し、エラー訂正を行い、RBEC(Received Bits Error Recovered)にエラー訂正をした情報ビットを出力します。エラー訂正用ビットもエラー訂正処理を行うことが可能ですが、それを出力するしないは設計者の自由とします。
ERRCNTは11ビットの情報ビットに対するエラーの累積値を示すもので、一応8ビットすなわち、255までとしますが、自由に変更してもかまいません。
内部EN信号Internal EN信号は、STARTの入力サイクルから21サイクルの間’1’となり、その後の21サイクルは’0’となる信号である。この信号は図4、図7のEN信号と対応しており、EN='1'の区間はシンドロームレジスタへの値の取り込み、EN='0'の区間はエラー検知信号ERROR_FOUND信号の発生区間を意味する。
初心者用RECEIVERは以下のピン配置をもつこととします。
|
Receiver |
|||
| 信号名 | 入出力 | ビット幅 | 説明 |
| CLK | IN | 1 | クロック入力 |
| RESET | IN | 1 | ’1’でリセット |
| START | IN | 1 | 情報ビットの先頭位置を示す |
| RBWE | IN | 1 | エラー付の受信信号 |
| START2 | OUT | 1 | エラー訂正後の情報ビットの先頭位置を示す |
| RBEC | OUT | 1 | エラー訂正処理された受信信号 |
表10 RECEIVERの初心者用ピン配置
以下に送信機TRANSMITTER、エラーカウント機ERRORCNT、全体シュミレーション、ならびに受信機のテンプレートのVHDLファイルをリンクします。必要に応じて修正して使用してください。
送信機: transmitter.vhd
エラーカウント機: errorcnt.vhd
全体シミュレーション: test_dcc21.vhd
設計すべき受信機のテンプレート: receiver.vhd
中級者用RECEIVERは初心者用と同じピン配置をもつこととしますが、以下に示すエラー訂正回路に以下に示す改良を行います。
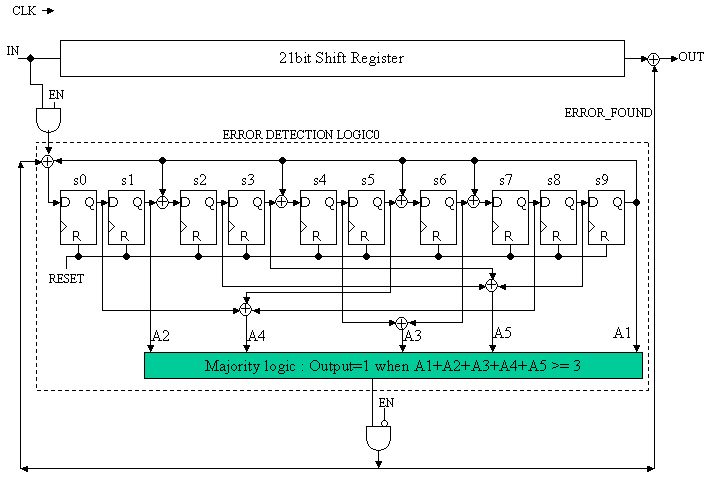
図7 改良されたERROR DETECTION LOGIC
図7は図4のERROR DETECTION LOGICのMajority logicからのエラー検知信号ERROR_FOUNDをシンドロームレジスタにフィードバックしたものである。すなわち、Majority Logicにてエラーの発生が検知されたら実際にエラー訂正をおこなうので、そのエラー訂正に対応してシンドロームを変更する。このようにすると、うまくすべてのエラーが訂正されたならば、すべてのシンドロームビット s0, s1, ... , s9はすべて0となる。
上記改良をすることで、エラーの修正能力が向上する。
上級者用はSTART信号入力がない、表11のピン配置でかつ、中級者用の改良されたエラー訂正方式とします。
START信号がないので、最初の21サイクルの同期信号によりSTART信号を発生させる必要があります。ただし、同期信号にもエラーが発生するのでやや工夫が必要です。
|
Receiver |
|||
| 信号名 | 入出力 | ビット幅 | 説明 |
| CLK | IN | 1 | クロック入力 |
| RESET | IN | 1 | ’1’でリセット |
| RBWE | IN | 1 | エラー付の受信信号 |
| START2 | OUT | 1 | エラー訂正後の情報ビットの先頭位置を示す |
| RBEC | OUT | 1 | エラー訂正処理された受信信号 |
表11 RECEIVERの上級者用ピン配置
琉球大学以外からの参加の場合、同一のシノプシスデザインコンパイラの論理合成用ライブラリを使用することが困難であるので、以下のような多段EXOR回路を例に従って合成し最適化して頂き、その1段あたりの遅延時間を単位時間としてスピードの単位とする。
多段EXOR回路のVHDLソース例:50入力のEXOR回路
この例では6段のEXOR段が合成され、クリティカルパス遅延はreport_timingコマンドにより7.17であったので、7.17/6=1.195を単位(UNIT)とする。
例えば、ある遅延が20ならば、20/1.195=17.74UNIT遅延とする。
琉大情報のライブラリ使用者は上記値で換算で換算すればよい。
ちなみに面積はreport_areaコマンドのtotal cell areaにある。
レポートには以下の内容を含めること。また、ページ数を少なめにコンパクトにまとめること。
| 表紙 | 1 | 代表者の氏名、チーム名、大学院修士/大学学部生/高専生の区別 |
| 2 | 共同設計者全員の名前(最高3名まで)、学籍番号、学年、学校名、住所、電話、email等連絡先 | |
| 3 | 全員のTシャツの希望サイズ | |
| 4 | 取り組んだ課題(LEVEL1/LEVEL2/LEVEL3) | |
| 内容 | 1 | 設計した回路ブロックの構成説明(ブロック図と説明) |
| 2 | 設計した回路ブロックの動作説明(動作波形図やパイプライン動作等の説明) | |
| 3 | 工夫した点、オリジナリティを出した点(アピールが重要!) | |
| 4 | クリティカルパスのスピード、論理合成後の回路規模 | |
| 5 | VHDLもしくはVerilogのコード | |
| 6 | 正常動作しているVHDL/Verilogシミュレーション波形 | |
| 7 | その他自由意見など |
レポートはPDFファイルにて下記にEMAILにて提出すること!
他の形式での提出希望あれば、相談してください。
締め切りは2002年2月15日(金)必着です。
ENJOY HDL! 沖縄で会おう!