AES課題用ガロア体の補足
琉球大学 情報工学科 和田知久
ガロア体
- 整数の集合は{..., -1, 0, 1, 2,
...}と無限の要素から成り立っているのに対して、
ガロア体とは整数を素数(たとえば5)で除算した余りの集合{0,
1, 2, 3, 4}のように
要素が有限で四則演算が閉じている集合である。
例(1) 整数を5で除算した余りの集合{0,1,2,3,4}
- 整数を5で除算した余りの集合{0,1,2,3,4}
- 加算のすべての組み合わせを以下に示す。
- 全組み合わせに対して、加算の結果は{0,1,2,3,4}の要素であり、加算に関して閉じている。
- 加算の結果の各行、列に{0,1,2,3,4}の要素がすべて含まれているので、減算に関しても閉じている。(加算の結果(表の右下の5x5の要素)から好きな数字(水色の数字)を減算した時の結果を表から読み取れる。)
| 加算 |
0 |
1 |
2 |
3 |
4 |
| 0 |
0 |
1 |
2 |
3 |
4 |
| 1 |
1 |
2 |
3 |
4 |
0 |
| 2 |
2 |
3 |
4 |
0 |
1 |
| 3 |
3 |
4 |
0 |
1 |
2 |
| 4 |
4 |
0 |
1 |
2 |
3 |
- 乗算のすべての組み合わせを以下に示す。
- 全組み合わせに対して、乗算の結果は{0,1,2,3,4}の要素であり、乗算に関して閉じている。
- 0以外の乗算の結果の各行、列に{0,1,2,3,4}の要素がすべて含まれているので、除算に関しても閉じている。(0では当然除算できない)
| 乗算 |
0 |
1 |
2 |
3 |
4 |
| 0 |
0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
1 |
2 |
3 |
4 |
| 2 |
0 |
2 |
4 |
1 |
3 |
| 3 |
0 |
3 |
1 |
4 |
2 |
| 4 |
0 |
4 |
3 |
2 |
1 |
- ということで、整数を5で除算した余りの集合{0,1,2,3,4}はガロア体です!
例(2) 整数を4で除算した余りの集合{0,1,2,3}
- 整数を4で除算した余りの集合{0,1,2,3}
- 加算のすべての組み合わせを以下に示す。
- 全組み合わせに対して、加算の結果は{0,1,2,3}の要素であり、加算に関して閉じている。
- 加算の結果の各行、列に{0,1,2,3}の要素がすべて含まれているので、減算に関しても閉じている。
| 加算 |
0 |
1 |
2 |
3 |
| 0 |
0 |
1 |
2 |
3 |
| 1 |
1 |
2 |
3 |
0 |
| 2 |
2 |
3 |
0 |
1 |
| 3 |
3 |
0 |
1 |
2 |
- 乗算のすべての組み合わせを以下に示す。
- 全組み合わせに対して、乗算の結果は{0,1,2,3}の要素であり、乗算に関して閉じている。
- 0以外の乗算の結果の各行、列に{0,1,2,3}の要素がすべて含まれていないので、除算に関して閉じていない。(この表から1÷2、3÷2は計算できない!!!)
| 乗算 |
0 |
1 |
2 |
3 |
| 0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
1 |
2 |
3 |
| 2 |
0 |
2 |
0 |
2 |
| 3 |
0 |
3 |
2 |
1 |
- ということで、整数を4で除算した余りの集合{0,1,2,3}はガロア体ではない!
- 除算を素数でやらないとだめです!
ここまでは非常に簡単!
GF(2)
- コンピュータやデジタル通信では、通常1と0の2つのシンボルが用いられる。これらに対して法2(mod
2、2で除算した余り)の加算、乗算は以下のようになります。
- すなわち、加算はEXORで、1+1=0ですので1=−1となることに注意してください。
- すなわち、乗算はANDということになります。
- 上記表より、減算、除算についても閉じていますので、この2つの元(要素)からなる体を2元体と呼び、GF(2)と表します。
GF(2w)
- 2^w(2のw乗)の要素(元)をもつ体は2^wのガロア拡大体と呼び、
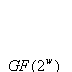 と表します。
と表します。
- GF(2)上の元{0,1}を係数にもつw次の既約多項式p(x)を考える。
- 新しくαという元を考え、p(α)=0と仮定します。
- 既約多項式p(x)をうまく選べば、
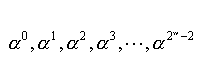
なる要素はすべて異なり、
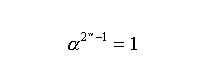
を成立させることができる。
- これに零元を加えてると、
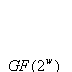 の元の集合となる。
の元の集合となる。
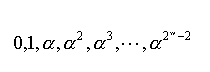
GF(24)
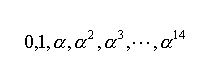
- 各要素は多項式に対応し、その係数は4桁の2進数となる。
- α^4+α+1=0なので、α^4=-α-1=α+1となります。(各係数はGF(2)ですので、1=−1です。)
- この関係をもちいてα^mは3次以下の多項式に変形できます。この多項式の係数が4ビットの2進数に対応します。
| 指数 |
|
α^3 |
α^2 |
α^2 |
α^0 |
対応する整数値 |
| -∞ |
0 |
0 |
0 |
0 |
0 |
0 |
| 0 |
1 |
0 |
0 |
0 |
1 |
1 |
| 1 |
α |
0 |
0 |
1 |
0 |
2 |
| 2 |
α^2 |
0 |
1 |
0 |
0 |
4 |
| 3 |
α^3 |
1 |
0 |
0 |
0 |
8 |
| 4 |
α^4=1+α |
0 |
0 |
1 |
1 |
3 |
| 5 |
α^5=α(1+α)=α+α^2 |
0 |
1 |
1 |
0 |
6 |
| 6 |
α^6=α(α+α^2)=α^2+α^3 |
1 |
1 |
0 |
0 |
12 |
| 7 |
α^7=α(α^2+α^3)=α^3+α^4=1+α+α^3 |
1 |
0 |
1 |
1 |
11 |
| 8 |
α^8=α(1+α+α^3)=α+α^2+α^4=1+α^2 |
0 |
1 |
0 |
1 |
5 |
| 9 |
α^9=α(1+α^2)=α+α^3 |
1 |
0 |
1 |
0 |
10 |
| 10 |
α^10=α(α+α^3)=α^2+α^4=1+α+α^2 |
0 |
1 |
1 |
1 |
7 |
| 11 |
α^11=α(1+α+α^2)=α+α^2+α^3 |
1 |
1 |
1 |
0 |
14 |
| 12 |
α^12=α(α+α^2+α^3)=α^2+α^3+α^4=1+α+α^2+α^3 |
1 |
1 |
1 |
1 |
15 |
| 13 |
α^13=α(1+α+α^2+α^3)=α+α^2+α^3+α^4=1+α^2+α^3 |
1 |
1 |
0 |
1 |
13 |
| 14 |
α^14=α(1+α^2+α^3)=α+α^3+α^4=1+α^3 |
1 |
0 |
0 |
1 |
9 |
| 15 |
α^15=α(1+α^3)=α+α^4=1 |
0 |
0 |
0 |
1 |
1 |
- 加算は以下のように、各桁ごとにEXORを行います。なぜなら、多項式なので、同じ次数の項のみ加算するのはあたりまえ。
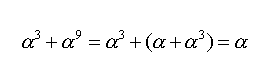
- 乗算は以下のように指数の加算になります。(ここでα^15=1が重要です!)
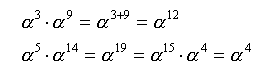
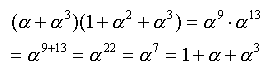
- すなわち、α+α^3(2進数で1010)をα^9(指数値で9)に変換し、加算を行い、
結果を逆変換(指数値から2進数)へ変換すると乗算ができます。
- この2進数→指数変換TABLEが gflog であり、
- 指数→2進数変換が gfilog になります。
- 2進数0000に対応する指数は”-∞”(負の無限大)であり、特別な処理が必要です。
AES用GF(28)用乗算器と逆数器の設計
http://www.ie.u-ryukyu.ac.jp/~wada/design04/spec_j.html
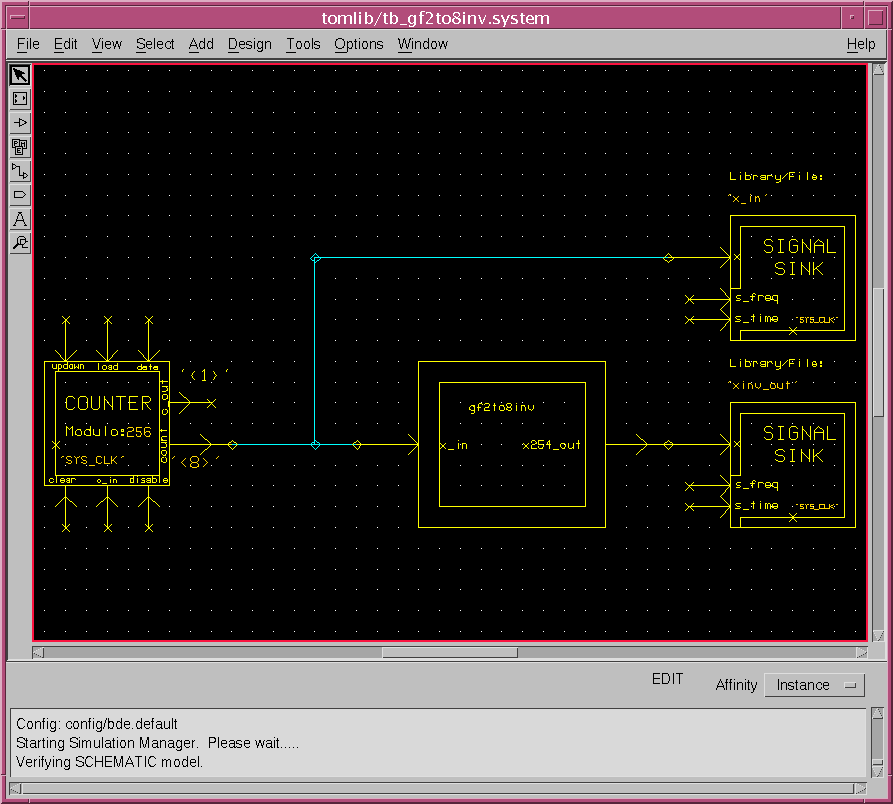
- セクション[4]に示したブール式をSPWのHDSを用いて設計してみました。分かりにくいですが、多数のANDとEXORで設計されています。(HDSはVHDLやVerilogHDLのようなハードウエア記述言語をグラフィカルに設計するツール)
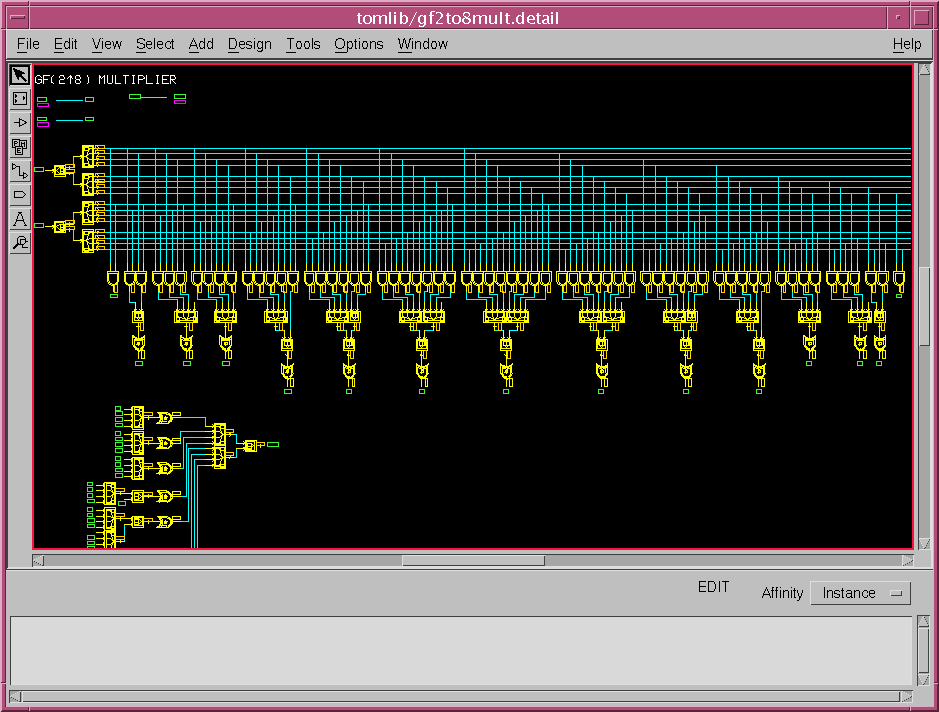
- 上記設計したGF(28)の乗算器をもちいて254乗の計算を、伊東・辻井のアルゴリズムによる逆元計算回路にて実装すると以下になります。
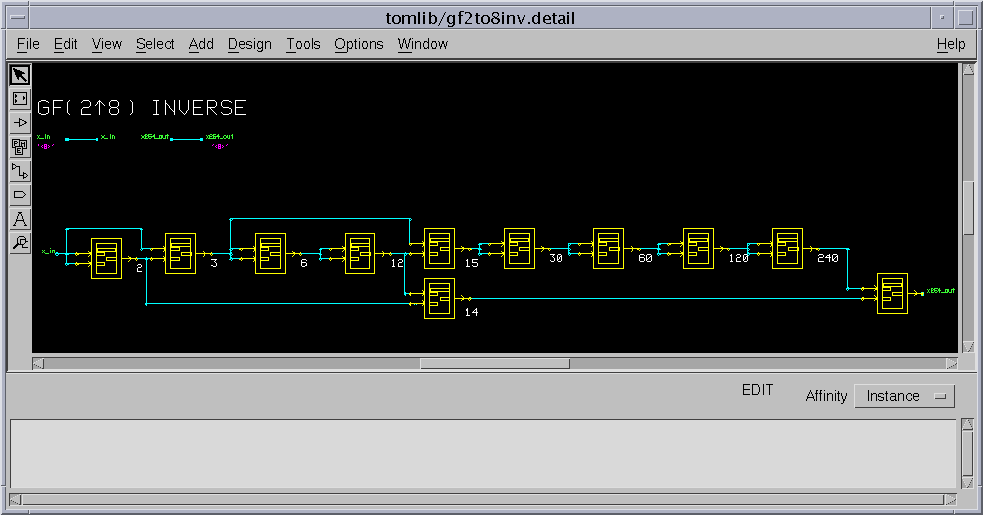
最終レポート事前課題1
1) http://www.ie.u-ryukyu.ac.jp/~wada/design04/spec_j.html の 表1 GF(28)の逆元テーブルをそのまま利用してGF(28)の逆数を計算する組み合わせ回路をVHDLにて設計し、最小面積とその時の動作スピードを求めよ
2) http://www.ie.u-ryukyu.ac.jp/~wada/design04/spec_j.html のセクション[3],
[4]で説明した(上記HDS設計の方式)方法を用いて、GF(28)の逆数を計算する組み合わせ回路をVHDLにて設計し、最小面積とその時の動作スピードを求めよ
3) 上記 1)と2)の結果を比較して議論せよ!
以上
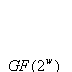 と表します。
と表します。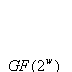 と表します。
と表します。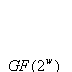 の元の集合となる。
の元の集合となる。