デジタルFMレシーバ　設計仕様書 (Ver 1.0)

琉球大学工学部情報工学科　和田　知久

[０]　はじめに

今回はデジタル方式のFMレシーバ回路の設計を行います。FMはFrequency Modulationすなわち、周波数変調の意味で、音声などのアナログ信号の値の変化（強弱）を正弦波の周波数の変化に変換して電波として伝送する方式です。FM変調は有名な方式なので多数の通信系の教科書に解説や回路に関する記述があります。しかしながら、よく教科書で紹介されている回路はアナログ方式の回路であり、今回はFM変調された正弦波信号をADC（アナログ−デジタル変換器）にてデジタル化したことを前提にデジタル方式のFM復調回路の設計を行います。

学生対象のコンテストですので小さめのデジタル回路を設計することを念頭に、なるべく簡単な回路構成要素を組み合わせてFM復調を行う回路を設計します。今回設計するデジタル方式のFMレシーバは入力信号に追随して同期する正弦波発生回路をベースとしています。一般的にはPLL（Phase Locked Loop）と言われる回路をデジタル回路で構成します。FM変調では正弦波の周波数が変化します。PLLはその周波数の変化する正弦波に同期するので、周波数値に比例する信号も同時に生成されます。まさにその信号を取り出せばFM復調を行えたことになります。

要求されている設計内容はHDL（VHDLもしくはVerilogHDL）による設計と論理合成です。特にシノプシス社の合成ツールを使用する必要はなく、FPGA等の合成ツールでも参加できます。HDL設計に興味のある学生はどしどし参加してください。また、余裕のある方はFPGA等で実装すれば、努力を認めて高い評価が得られると思います。FPGA等での実装もぜひトライしてみてください。

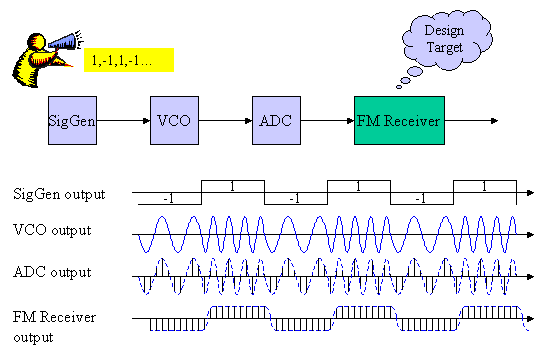
図１　システム図

図１に今回想定するシステムのブロック図を示します。システムは大きく分けて、送信信号生成部（SigGen）、そのSigGenの出力値に比例して周波数の変わるVCO (Voltage Controlled Oscillator）、アナログ−デジタル変換器（ADC）、そしてそのデジタル化されたFM信号を復調するFM Receiverから構成されます。図１では簡単のためにSigGenの出力は２値（１、−１）としていますが、0.5などのその他の値でもかまいません。その場合その値に対応する正弦波がVCOより出力されます。VCOは電圧制御型発振器であり、通常の回路構成では入力値は電圧信号で与えられるので、VCOという名前になっています。図１からわかるように、SigGenの値が”−１”の時にある低めの周波数の正弦波を生成し、”１”のときに高めの周波数の正弦波を出力しています。ADCはある一定のクロック周期ごとにアナログ波形の電圧値をデジタルの数値に変換します。図１ではデジタル化を示すために、波形を棒グラフで示しています。後に詳しく説明しますが、ADCの出力ビット幅を今回８ビットに設定していますので、棒グラフの棒の高さは28=256通りの値を取ることになります。FM Receiverはその８ビットの値を毎クロックごとに受け取り処理を行います。最終的にはFM復調した波形を出力します。

今回の課題はデジタル信号処理をデジタル回路を用いて実現します。デジタル回路で整数の演算を行うのは比較的分かりやすいのですが、ADC出力値は正、負の両方の値を取る小数点表現を用います。設計すべきことは比較的単純ですので、デジタル設計の知識のある学生は自信を持って、課題に取り組んでください。

[１]　フェイズ・ロック・ループ（Phase Locked Loop : PLL）

図２はPLLとそのループフィルター出力に低域通過フィルターLPFを接続したものであり、実はこれが今回設計するFM Receiverの全体回路構成になります。単純でしょう！

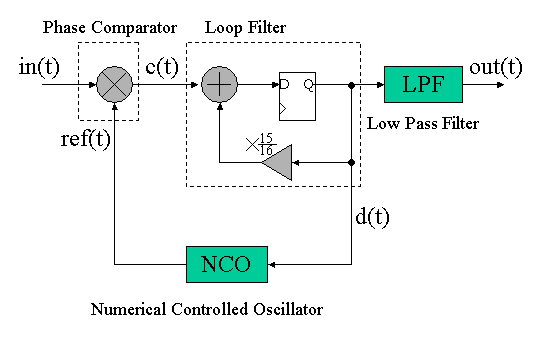
図2　PLL

ここでは幾つかの数式を用いてPLLの動作原理を説明します。まず入力信号はFM信号なので正弦波が入力されます。したがって、入力信号in(t)は

NCOはVCOと同様な発振器であり正弦波を出力します。ただし、その発振周波数は入力の値で制御されるので、値すなわちNumericalということで、NCOと呼ばれています。デジタル回路でのVCOとも言えます。PLL回路は図のようにフィードバックループを形成しており、ループ安定時にはNCO出力は入力とほぼ同じ周波数の正弦波を出力するので、出力信号ref(t)は以下のようになります。

ここでcosを用いているのは後の計算で、都合が良いからです。この２つの信号を乗算すると、以下のようにc(t)が求まります。

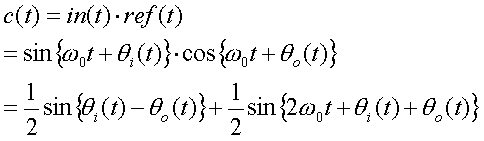
この１項目はin(t)とref(t)の位相成分の差であり、２項目は高周波の信号となります。ループフィルターでこの高周波成分を除去することにより、位相差成分を検知することができます。これが、位相比較器（Phase Comparator）の仕事です。

ループフィルターは乗算結果c(t)とDフリップフロップの値に固定値α（=15/16=0.9375）を乗算したものを加算する回路になっています。したがって、c(t)がループフィルターに入力された時のループフィルターの出力は以下の式で与えられます。αは１以下の値なので、c(t)のこれまで平均のような演算です。ただし、古いデータほど影響力は小さくなります。

平均処理ですので、高周波成分をカットする特性をもつので、上記位相比較器の２項目をキャンセルする作用があります。

[２]　Numerical Controlled Oscillator : NCO

図３にNCOの回路構成を示します。

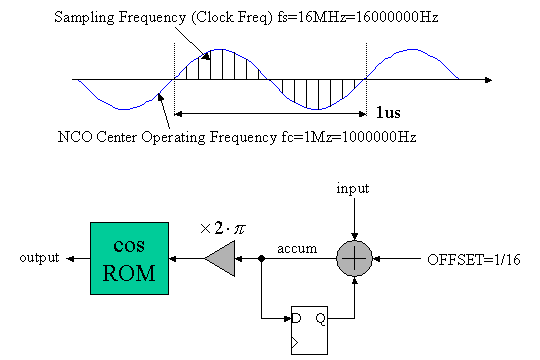
図３　NCO

詳細な説明を始める前に、システムの動作クロック周波数を16MHz=16,000,000Hzとし、NCOの出力する正弦波の中心周波数を1MHzとします。したがって、図中に示すように、１MHｚの正弦波（周期1us）では１周期の間に１６回のサンプリング点を持つことになります。

NCO回路はinput入力値＝０の場合に、１６クロック（サンプリング点）で１周期の正弦波を生成したいので、オフセット値として1/16をもつ回路になります。各クロックごとに、Dフリップフロップの値にオフセット値が加算されますので、ちょうど１６サイクルで1/16*16=1で加算器の出力accumは１増加します。これは累積計算なので、いわゆるアキュミュレータ(Accumulator)になっています。アキュミュレータ出力に対して2πを乗算し、cosの値をROM（ReadOnlyMemory）から取り出します。cos関数は2πで１周期なので、図中の正弦波をサンプリングした棒グラフのような出力が得られます。

ここでinputの値が正の値であれば、アキュミュレータの累積スピードは速くなり、１６サイクル以下でaccumは１増加し、１周期の正弦波が生成されるので、高い周波数を生成したことになります。また逆に、inputの値が負の値であれば、アキュミュレータの累積スピードは遅くなり、低い周波数を生成したことになります。すなわち、inputの値によって１MHｚ中心周波数を変化させることができます。

[３]　低域通過フィルタ（Low Pass Filter : LPF）

一般的にデジタルフィルターとして有名なのはFinite Impulse Response (FIR)フィルタです。図４(a)に１６TAPのFIRフィルターの構成を図示します。

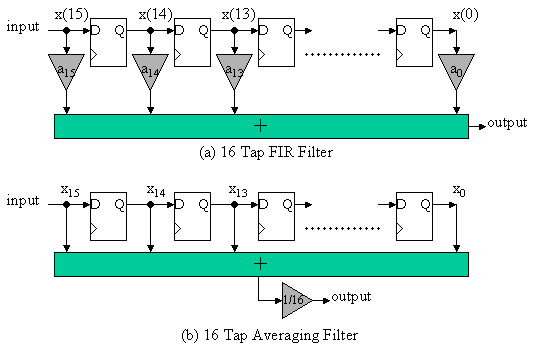
図４　FIR Filter

したがって、FIRフィルターの一般式は以下のように与えられます。

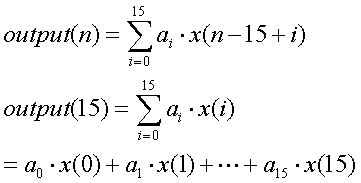
ここでa0, a1, ..., a15の乗算係数を適切に定めれば特性の良い低域通過フィルター（Low Pass Filter）を作ることができます。

しかしながら、これらの係数を最適すると図からも分かるように乗算器が１６個必要となり、回路規模面積がかなり増加します。今回の設計課題ではあまり良い特性ではないですが、回路の単純化のためにすべての係数を1/16＝0.0625に固定した平均フィルターを代用として使うことにします。

図４(b)にこの移動平均フィルターの回路図を示します。1/16の係数乗算は加算の後で共通化しています。実際には1/16はシフト操作で実現できるので、乗算器は不要となります。

[４]　固定小数点フォーマット

今回の課題では上記の1/16＝0.0625のような小数点以下の数をデジタル回路で取り扱う必要があります。たとえば４ビットの２進数”０１１１”ですが、小数点をどこの位置に置くかで表す値が変わってきます。たとえば、”０１．１１”ならば１０進数表現では＋１．７５、”０１１１．”ならば、１０進表現では＋７です。

また、４ビットの２進数ですが、それが符号無し数すなわち正または０の数を表しているか、２の補数表現で正または負の数を表しているかを区別する必要があります。”１１．１０”は符号無し数であれば、１０進表現で+3.50となり、２の補数表現であれば、１０進表現で-0.50となります。

すなわち、同じ４ビットの２進数でも、「小数点の位置」と「符号無し表現か２の補数表現か」を明確にしないとまったく異なった数に対応してしまいます。

ここではSignal Processing Workbenchで用いられている固定小数点の属性表記方法を解説し、用います。

<8,2,t>

と表記すると、その信号は

８　：　全体のビット数が８ビット
２　：　整数ビットが２ビット
ｔ　：　two's complement ということで２の補数表現、すなわち最上位ビットは符号ビットとなる

という意味です。したがって、”０１１０１１１１”なる８ビットの数の属性が<8,2,t>とすると、

0 1 1 0 1 1 1 1
符号ビット 整数部

小数部

ということになり、小数部は５ビットとなり、１０進表現では＋３．４６８７５に対応します。

<8,2,u>

と表記すると、その信号は

８　：　全体のビット数が８ビット
２　：　整数ビットが２ビット
u　：　unsignedということで、符号無し数すなわち負の数を表さない

という意味です。したがって、同じ８ビットの数”０１１０１１１１”の属性が<8,2,u>とすると、

0 1 1 0 1 1 1 1
整数部 小数部

ということになり、小数部は６ビットとなり、１０進表現では＋１．７３４３７５に対応します。

整数部のビット数が多いほど表現できる最大数すなわちレンジが大きくなり、小数部のビット数が多いほど表現できる最小数が小さくなり、解像度が向上します。

以下の表１に４ビットの数が<4,2,u>の属性を持つ場合と<4,1,t>の属性を持つ場合の１０進表現を示します。

表１　属性による値の違い

4ビットの数 属性<4,2,u>の場合の
１０進表現		 属性<4,1,ｔ>の場合の
１０進表現
0000 +0.00 +0.00
0001 +0.25 +0.25
0010 +0.50 +0.50
0011 +0.75 +0.75
0100 +1.00 +1.00
0101 +1.25 +1.25
0110 +1.50 +1.50
0111 +1.75 +1.75
1000 +2.00 -2.00
1001 +2.25 -1.75
1010 +2.50 -1.50
1011 +2.75 -1.25
1100 +3.00 -1.00
1101 +3.25 -0.75
1110 +3.50 -0.50
1111 +3.75 -0.25

以下の表２に４ビット長の固定小数点の属性の幾つかの例と、対応する２進数、値のレンジ、解像度を示します。表２からもわかるように同じ４ビット長を用いて多様なレンジと解像度の数値を表現できます。当然のことですが、解像度を悪く大きな値にすると、より広いレンジを表すことができます。

表２　４ビット長の固定小数点の属性の幾つかの例と、対応する２進数、値のレンジ、解像度

　 属性 ２進数表現
Sは符号ビット
Xはデータビット		 レンジ 解像度
整数 <1,1,u> X. 0 to 1 1
<4,4,u> XXXX. 0 to 15 1
<4,3,t> SXXX. -8 to 7 1
小数 <4,0,u> .XXXX 0.0 to 0.9375 0.0625 (1/16)
<4,0,t> S.XXX -1.00 to +0.875 0.125 (1/8)
その他 <4,2,u> XX.XX 0.0 to 3.75 0.25 (1/4)
<4,2,t> SXX.X -4.0 to + 3.5 0.5 (1/2)
<4,5,u> XXXX0. 0 to 30 2
<4,5,t> SXXX00. -32 to 28 4
<4,-1,u> .0XXXX 0.0 to 0.46875 0.03125 (1/32)
<4,-1,t> S.SXXX -0.5 to +0.4375 0.0625 (1/16)

[５]　デジタルFMレシーバー回路構成

図５にデジタルFMレシーバの全体回路構成の一例を示します。以下の回路構成で正常に動作することは確認済みです。すでにこれまでのセクションで各回路の動作原理を紹介したので、各回路の意味は理解できると思います。

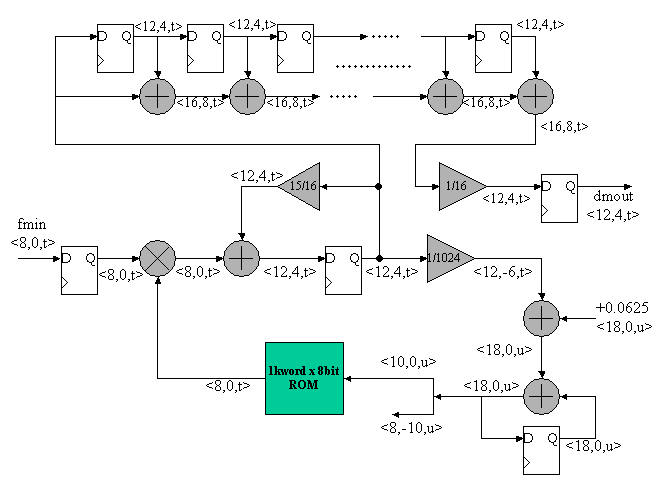
図５　デジタルFMレシーバの回路図の一例

図６にシミュレーション波形を示します。

上段から、１，−１の送信データの繰り返し、それをFM変調したもの、デジタルFMレシーバが生成した正弦波形（１Kwx8bit ROMの出力）、Phase comparatorすなわち乗算器の出力、アキュミュレータの出力、そしてFIRフィルターの出力であるdmoutの波形を示している。本来サンプリングされた値であるが、表示上ではその値を直線でつないで表示しています。

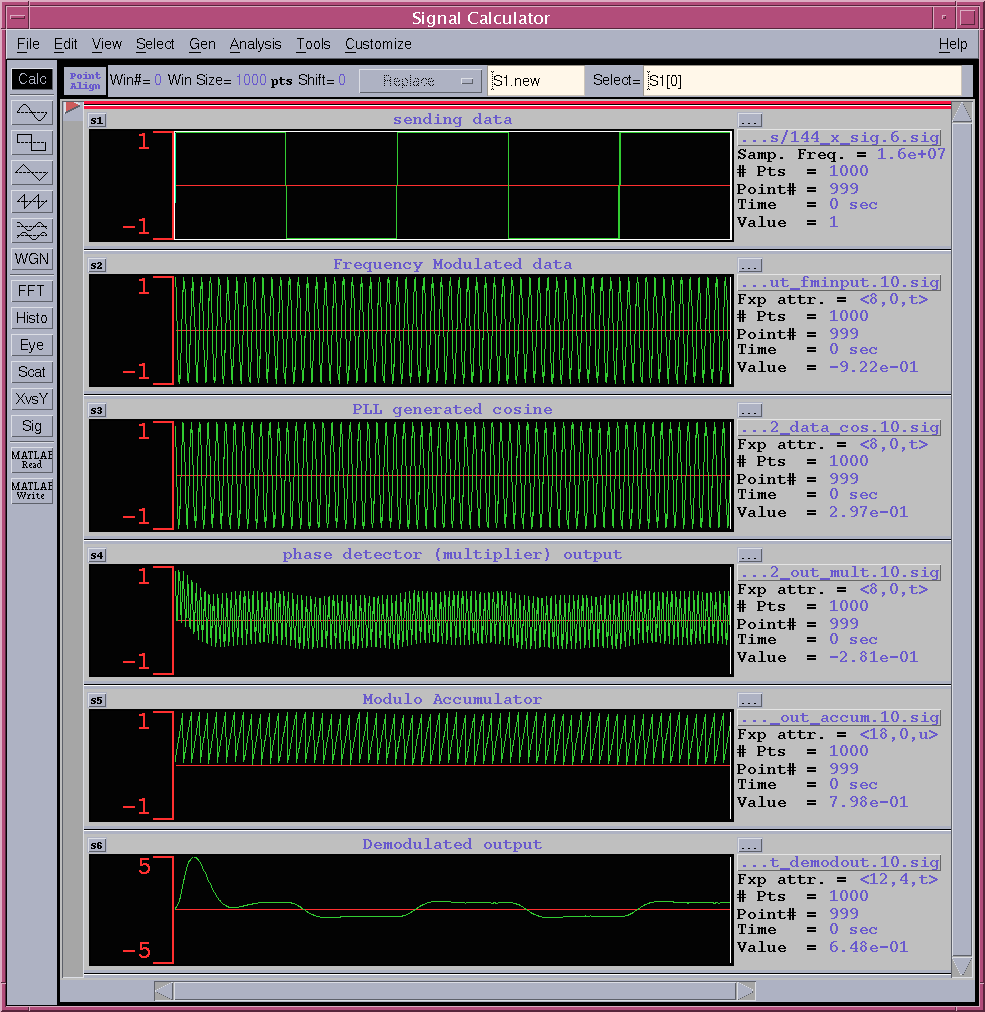
図６　シミュレーション波形

　

シミュレーションの初期にdmoutの値が大きくオーバーシュートしていますが、これは同期途中であり、その後正常な復調動作をしていることがわかります。図７に一部の拡大図を示します。

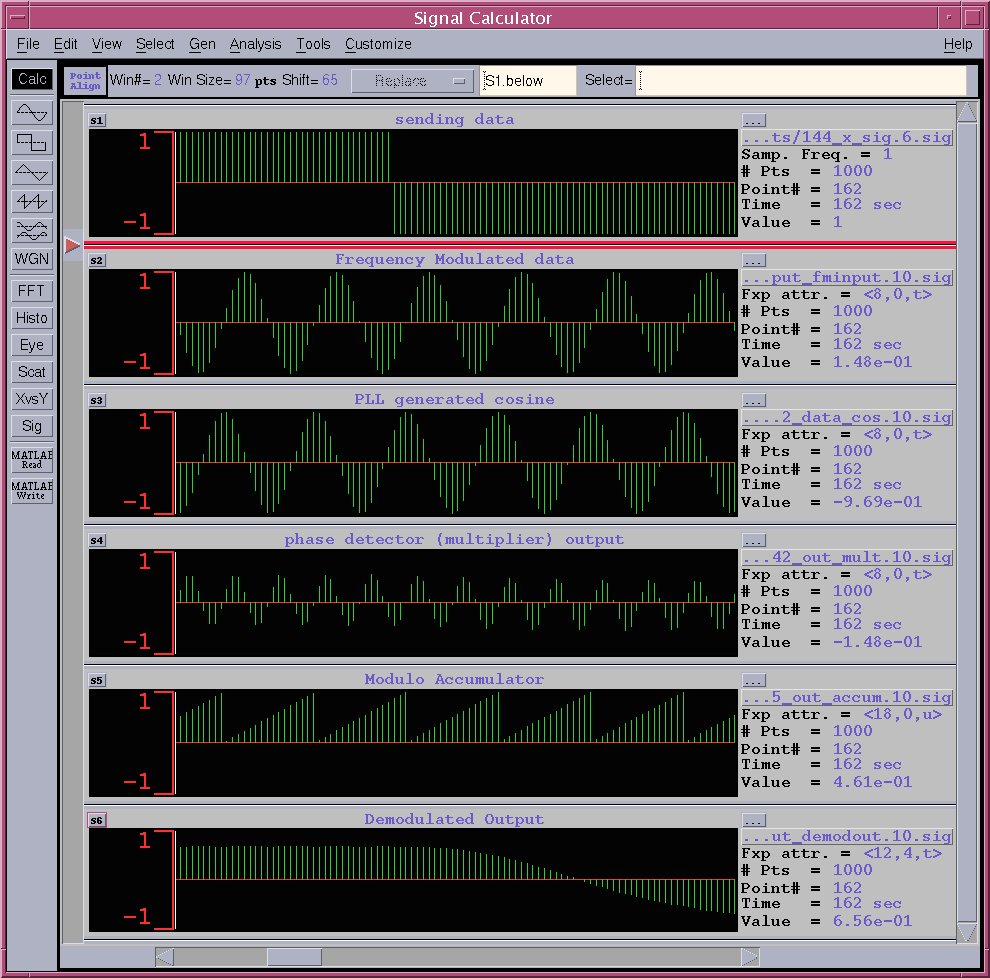
図７　拡大シミュレーション波形

図７ではデジタルの値を棒グラフ表示し、デジタル処理らしい表示にしています。

[６]LEVEL1：基本課題

基本課題では図６に示すように、送信データとして１、−１の繰り返しデータを変調したFM波形の復調が正常動作することが最低条件です。表３にFMReceiverの入出力信号ビット幅を示します。これを基本としますが、変更してもかまいません。

表３　基本課題用ピンリスト

FMRX
信号名 入出力 ビット幅 説明
CLK IN １ クロック入力
RESET IN １ ’１’でリセット
FMIN IN ８ 入力データ　属性は<8,0,t>
DMOUT IN １２ 復調波形出力　属性は<12,4,t>

　

以下に図６の上から２段目に対応するFM変調データをリンクます。各行に属性<8,0,t>の８ビットデータが1000点分あります。

また、以下に1024w X 8bitのROMのデータをリンクします。address=0 〜 1023に対応して、一周期分のcosの値すなわち、data = cos (2*π*address/1024)の８ビットの値が属性<8,0,t>で格納されています。COSINEの値ですので、簡単に生成することもできますが、念のためにリンクしておきます。

図５の回路をベースに回路数を削減したり、高速化などを行ってください。一応表３の入出力ピンを決めていますが、必要に応じて変更してもOKです。

　

[７]LEVEL2:上級課題

上級編では送信データとして、−１から１の範囲で変化する連続値（三角波形）をFM変調したものの復調ができることが最低条件です。図８に三角はの送受信のシミュレーション波形を示します。FM復調出力がほぼ三角波になっていることが確認できます。図８の上から２段目に対応するFM変調データをリンクます。

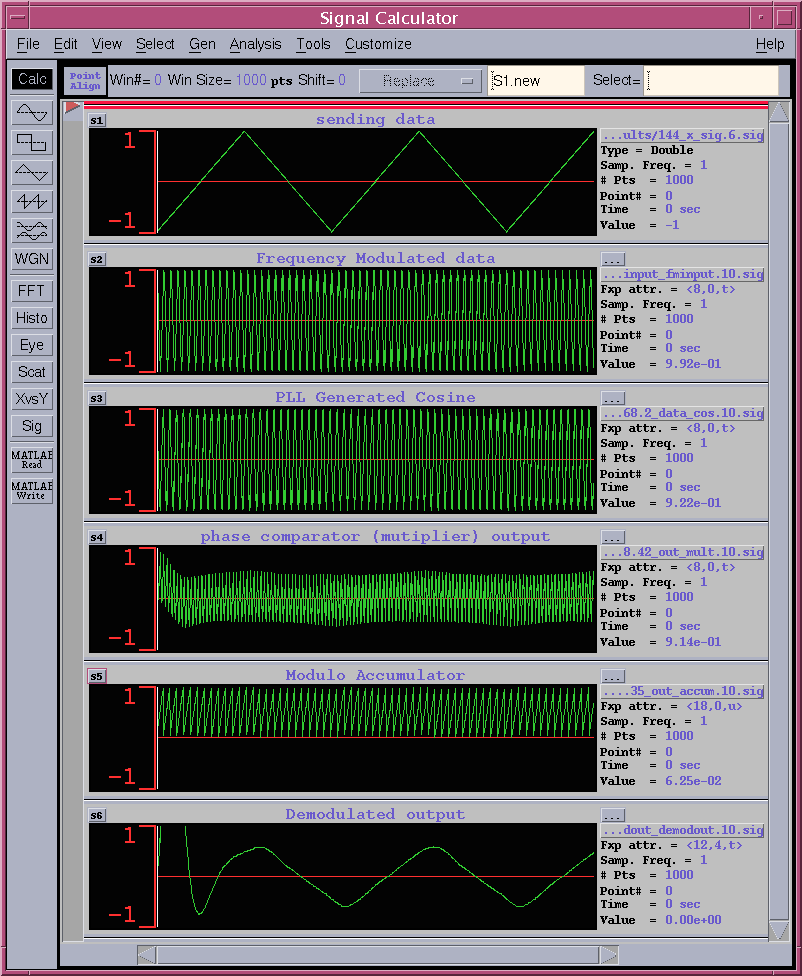
図８　三角波のFM送受信

　

[８]　スピードと面積の単位

琉球大学以外からの参加の場合、同一のシノプシスデザインコンパイラの論理合成用ライブラリを使用することが困難であるので、

とします。

具体的には、以下のような多段EXOR回路を例に従って合成し最適化し、その１段あたりの遅延時間を単位時間としてスピードの単位とします。

多段EXOR回路のVHDLソース例：５０入力のEXOR回路

合成語の回路図　PDF,　PS

この例では６段のEXOR段が合成され、クリティカルパス遅延はreport_timingコマンドにより７．１７であったので、７．１７/６＝１．１９５を単位（1UNIT_DELAY）とします。

また、面積はreport_areaコマンドのtotal cell areaは147.0であり、EXORゲイト数は49個であるので、１４７．０/４９＝３．０を単位（1UNIT_AREA）とします。

[９]　レポート

レポートには以下の内容を含めるてください。また、ページ数を少なめにコンパクトにまとめてください。

表紙 １ 代表者の氏名、チーム名、大学院修士/大学学部生/高専生の区別
２ 共同設計者全員の名前（最高３名まで）、学籍番号、学年、学校名、住所、電話、email等連絡先
３ 全員のTシャツの希望サイズ
４ 取り組んだ課題（LEVEL1／LEVEL2）
内容 １ 設計した回路ブロックの構成説明（ブロック図と説明）
２ 設計した回路ブロックの動作説明（動作波形図やパイプライン動作等の説明）
３ 工夫した点、オリジナリティを出した点（アピールが重要！）
４ クリティカルパスのスピード、論理合成後の回路規模
５ VHDLもしくはVerilogのコード
６ 正常動作しているVHDL/Verilogシミュレーション波形
７ その他自由意見など

レポートはPDFファイルにて下記にEMAILにて提出すること！

他の形式での提出希望あれば、相談してください。

wada@ie.u-ryukyu.ac.jp

締め切りは２００５年１月３１日（月）必着です。

[１０]　審査のポイント

[１１]　謝辞

今回の課題作成にあたり、回路案をご提供頂いた（株）トヨタIT開発センター　横山　明久様に感謝いたします。

本LSI設計コンテストの学生部門の企画・実行、および沖縄での発表会は

主催：LSIコンテスト実行委員会
共催：株式会社沖縄産業振興センター
協賛： ソニーLSIデザイン株式会社、九州経済局

です。

ENJOY　HDL!　沖縄で会いましょう！

コンテストTOPページへ戻る