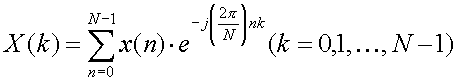
2006/8/30 ver 1.0作成
琉球大学工学部情報工学科 和田 知久
「LSIデザインコンテストin沖縄」も早いもので、今回で10年目を迎えることになりました。1998年に第一回のLSIデザインコンテストが開始された時は、琉球大学工学部情報工学科内部での学生コンテストでしたが、回を重ねるごとに、学外、国外と参加者の枠が広がりました。最近数年には、約100名の学生の参加があり、3月の沖縄での発表会では10件前後の優秀デザインの発表会を行い、みんなで大いに盛り上がっています。2001年度よりCQ出版社と協力を開始し、デザインウエーブ設計コンテストとしては第7回となります。
そして設計するテーマも時代を反映した内容を努めて出題するように心がけてきました。第1回の「LSIデザインコンテストin沖縄」を立ち上げてくださったのは、当時、琉球大学工学部情報工学科学科長の翁長健治教授(現琉球大学名誉教授)であり、LSI関連教育担当の尾知博教授(現九州工業大学教授)でした。当時、和田は三菱電機の社員であり1999年5月に琉球大学に転職してから、このコンテストを引き継ぎ運営させていただいています。今回10年目ということで、以下表1に過去の「LSIデザインコンテストin沖縄」設計課題を示します。
| 回 | 西暦 | 設計テーマ | 応用 |
| 第1回 | 1998年 | KUE-チップ | マイクロプロセッサ |
| 第2回 | 1999年 | RSA暗号デコーダ | 暗号 |
| 第3回 | 2000年 | リードソロモンCODEC演算エンジン | CD、デジタル通信/放送用エラー訂正 |
| 第4回 | 2001年 | デジタルCDMAレシーバー | 携帯電話、無線LAN |
| 第5回 | 2002年 | 差集合巡回符号エラー訂正回路 | TVの文字放送、地上デジタル放送 |
| 第6回 | 2003年 | 静的ハフマン符号用可変長デコーダ | 音声圧縮、画像圧縮、動画圧縮 |
| 第7回 | 2004年 | 共通鍵暗号AES用SubByte変換回路 | 無線LAN、通信暗号化 |
| 第8回 | 2005年 | デジタルFMレシーバー | 無線通信・放送 |
| 第9回 | 2006年 | 2次元積符号繰り返しデコーダ | 広域無線LAN |
| 第10回 | 2007年 | 64点高速フーリエ変換回路 | 信号解析、OFDM通信、無線LAN |
さて、第10回の設計テーマですが、デジタル信号処理では必ず登場する高速フーリエ変換回路(Fast Fourier Transform Circuit)の設計です。高速フーリエ変換は離散フーリエ変換(DFT)を高速に計算する手法であり、計算式自体は単純であり、以下に示す式になります。今回は802.11a/g/nなどのワイヤレスLANでよく使われているサイズということで、64点のFFTすなわち、以下の式でN=64の場合になります。
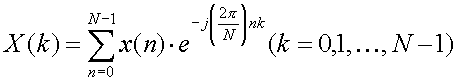
離散フーリエ変換の定義式は単純ですが、入力となるx(n)信号は、64点あり、またすべて複素数であり、出力X(k)も64点の複素数ということになります。このコンテストは学生対象のコンテストですので、学生対象対象としては64点は丁度良いサイズと考えています。以下にFFTについての詳細や、デジタル回路での実現方法を丁寧に説明しますので、これまで、上記式は知っていても物理的イメージが湧かなかった学生にも良い教材になると思います。要求されている設計はHDL(VHDLもしくはVerilogHDL)による設計と論理合成です。特にシノプシス社の合成ツールを使用する必要はなく、FPGA等の合成ツールでも参加できます。HDL設計に興味のある学生はどしどし参加してください。また、余裕のある方はFPGA等で実装すれば、努力を認めて高い評価が得られると思います。FPGA等での実装もぜひトライしてみてください。
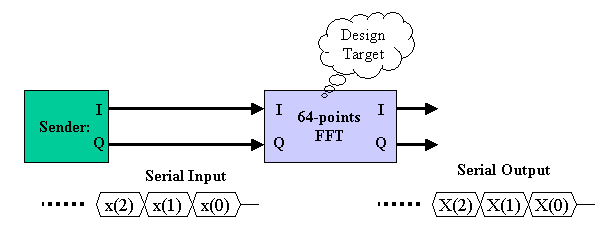
図1 システム図
図1に今回想定するシステムのブロック図を示します。システムは大きく分けて、送信信号生成部(Sender)、そのSenderの出力信号を高速フーリエ変換するFFT部から構成されます。複素数の信号はそれぞれ、実数部分をIポート、虚数部分をQポートを使用します。64ポイントの信号入力が必要で、図に示すように64点がシリアルに入力されることを想定し、FFTされた出力信号もシリアルに出力されます。
図1では、示されていませんが、64点の先頭の信号を示すフラグ信号も与えられ、64点の先頭位置をFFT回路は把握することができます。
離散フーリエ変換は通常スペクトル解析に使用されます。イメージとしては以下のようになります。x(n)は解析するN点の区間で、ほぼ1周期の正弦波となっています。これを離散フーリエ変換(DFT)を行うと、右の図のようにk=1に大きな成分が現れ、元信号x(n)にはk=1の周波数成分が多く含まれることがわかります。このような解析をスペクトラム解析と呼びます。よく見るとk=N-1の部分にも大きな成分があります。DFTでは、N点の点が周期的に繋がっている関係にあり、k=N-1は実はk=-1の周波数を示すことになります。負の周波数とは理解が困難かも知れませんが、x(n)の1周期の波形は、K=-1の周波数とK=1の周波数成分からできていると考えることができます。
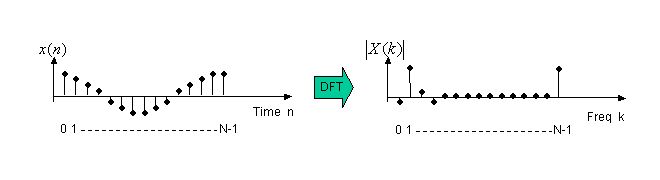
図2 DFTによるスペクトラム解析
以下に離散フーリエ変換(DFT)とその逆変換である逆離散フーリエ変換(IDFT)の式を示しておきます。N点のx(n)信号をN点のX(k)信号に変換するのが、DFTであり、その逆がIDFTです。DFTを高速に演算する方式がFFTであり、IDFTを高速に演算する方法がIFFTですので、以下、DFTをすべてFFT、IDFTのことをすべてIFFTと呼ぶことにします。ただし、FFTではNは2の指数乗である制約があります。
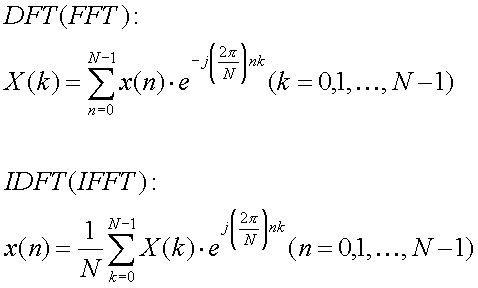
2つの式をよく見ると以下の2つの違いがあります。
1) 最初に1/Nがあるかないか
2) 指数のjの前の符号
したがって、2つの変換は非常に良く似たものであり、以下の図に示すように、FFT回路があれば、IFFTを簡単に実現することができます。
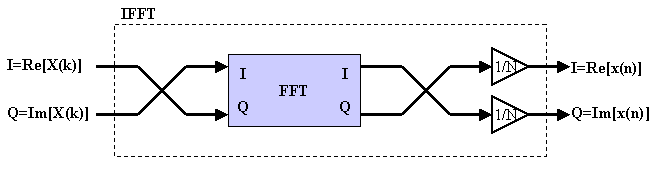
図3 FFT(DFT)によるIFFT(IDFT)の実現
さて、今回設計するFFTの式を見て行くことにしましょう。ここでは式をTwiddle Factor WNを用いて変形しています。
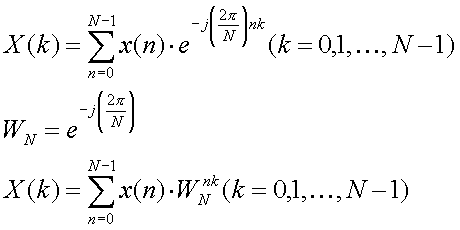
Twiddleとは指でぐるぐる回すという意味ですので、回転を示すものです。ここで2次元平面を用いて、このTwiddle Factor WNを説明します。
Eulerの公式より以下が成立します。これをX軸を実数(Real)軸、Y軸を虚数(Imaginary)軸とする2次元平面に示すと以下のようになります。
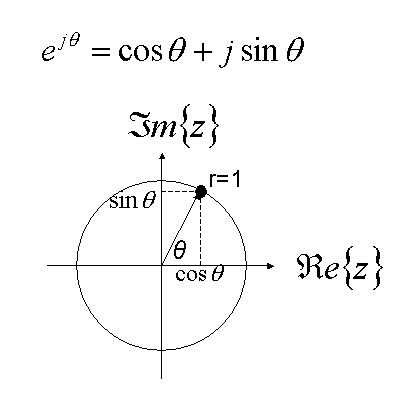
図4 Eulerの法則と2次元複素平面での表示
すなわち、ejθという関数はθを変化させることによって、半径1の円周を回転する点を示すことになります。フーリエ変換ではこの複素平面での回転を使って、波を解析します。したがって、半時計回りの回転は正の周波数に対応し、時計回りの回転は負の周波数に対応することになります。
したがって、Twiddle Factor WNを複素平面に示すと図5のようになります。実際FFTの式ではこのTwiddle Factor WNは指数乗されますので、指数が増加すると、図に示すように、複素平面で時計方向の回転をすることになります。
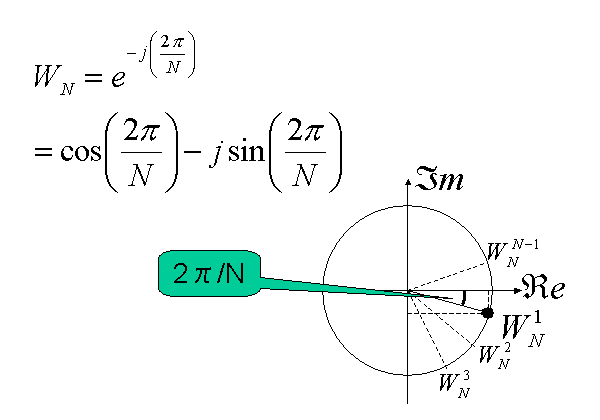
図5 Twiddle Factorの意味
以下のFFT演算の内容をさらに理解するために、4点FFTを行列表現したものを図6に示します。N=4ですので、行列表現では4X4のTwiddle Factorが並ぶ行列ができます。Twiddle Factorは図6右に示すように、W0, W1,....の順で複素平面状の半径1の円周を回転します。
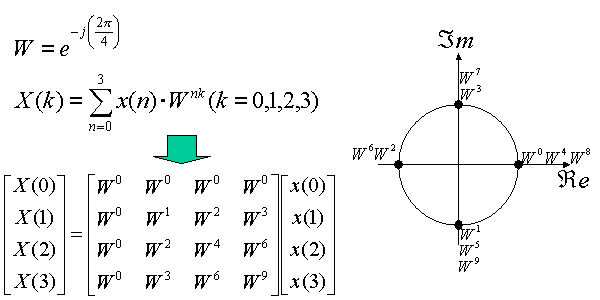
図6 4点FFTの行列表現
このTwiddle
Factorの行列に数値を入れたものを図7に示します。一行目は1が並び、これは同じ値が続く周波数0の回転に対応しています。2行目は、1,
-j, -1,
jとなり、これは複素平面状での負の方向への1回転を示しています。3行目は1,
-1, 1,
-1となり、これは複素平面状での2回転を示しています。3行目は、1,
j, -1,
-jとなり、これは負の方向への3回転ですし、正の方向への1回転と考えることもできます。
すなわち、FFT演算とは複素数による回転を示す波形の周波数の異なるものそれぞれと、入力信号x(n)の内積計算をしていることになります。
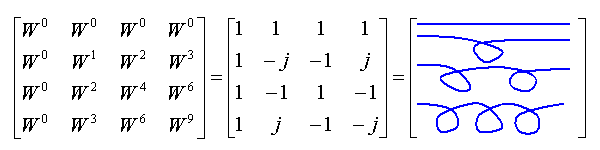
図7 4点FFTの行列表現
通常FFT演算で教科書を見れば、バタフライ演算が使われています。特にRADIX-2バタフライという演算が使用されています。しかしながら、このLSI設計コンテストでは、現実的に実装の観点から効率の良いRADIX-4(基底4)バタフライ演算を前提に、64点FFT回路の演算方式を紹介します。
64=43であるので、FFTにインデックスを以下のように変数変換します。各Σの加算個数は4個で、3重のΣからなる式に変形できます。この一つのΣが1ステージの処理となり、3段で全体の処理が行えます。
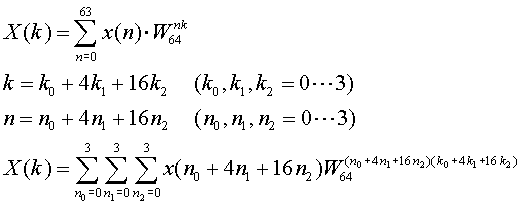
まず最初にn2に関するΣを展開し、変形ます。ここで、Twiddle Factor WNの性質、(WN)0=1, (WN)1N/4=-j, ( WN)2N/4=-1, ( WN)3N/4=j が用いられています。
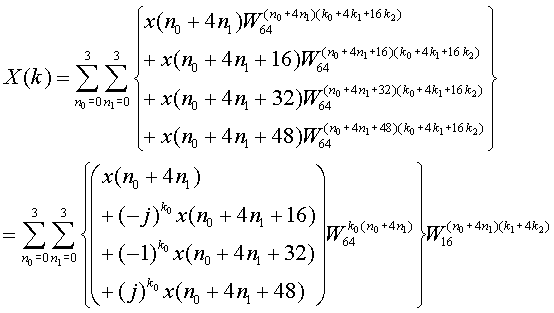
ここで、以下のようにx1をおくと、以下のようになります。
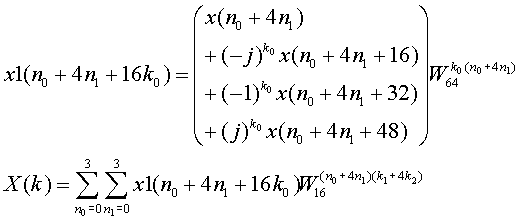
x1は4つの値に、jや-1などを掛けて、加算した後にTwiddle Factor を乗算しています。このx1の計算が第1ステージの演算となります。次に、このx1を入力として、上記計算を行えばX(k)が求まりますが、これは16点FFTの式となります。ただし、k0=0, 1, 2, 3の場合があり、16点FFTを4回計算する必要があります。
さらに上式を同様に変形します。
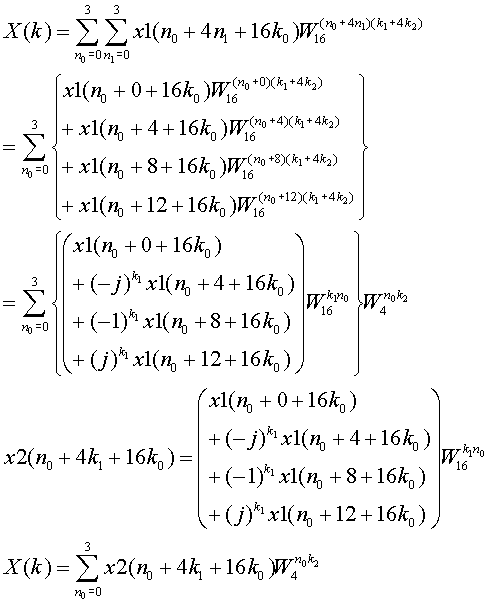
したがって、第2ステージの計算は上記x2を求めることになりますが、これはステージ1で求めた計算方法と同じであり、これをRADIX-4バタフライ回路と言います。
さらに上式を変形すると以下のようになり、同様のバタフライ演算になりますが、ただし、Twiddle Factor の乗算が不要となっています。
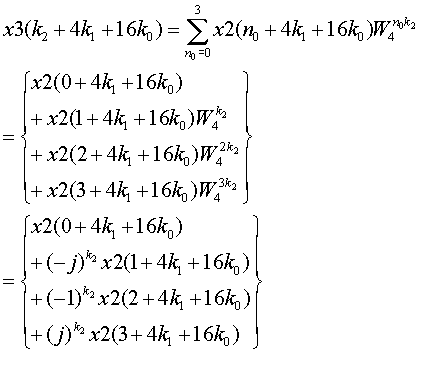
ここでx3(k2+4K1+16K0)が計算されましたが、本来のINDEX値は(k0+4K1+16K2)であり、INDEXの数値が入れ替わっています。したがって、INDEXの正しい出力を求めるためには、
以下で示されるような、関係で数値を並べ替える必要があります。
![]()
この計算アーキテクチャを図8に図示します。
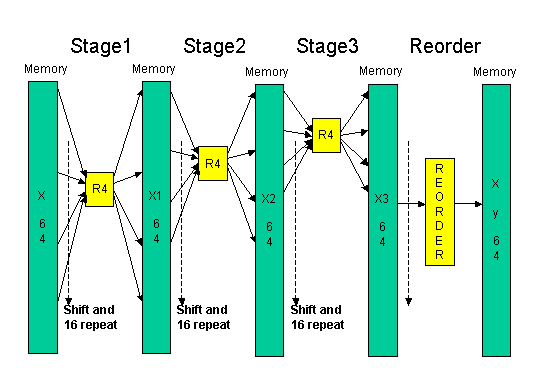
図8 RADIX-4 64点FFTアーキテクチャ
以下にここで説明したRADIX4による64点FFTの処理を行うMATLAB関数ファイルをリンクします。
MATLABによるRADIX4 64点FFT : myfft64.m
このFFT処理を理解するには、MATLABコードを読む方が容易です。また、MATLABでは配列のINDEXが0ではなく、1から始まるので、x, x1, x2, x3, yの値はINDEX=1が最初であることに注意してください。
今回のデザインコンテストでは、要はこのMATLABコードを回路で実現するので、FFTを完全に理解しなくても、このmyfft64.mを仕様として設計を進めることもできます。
以下にSCILABによるRADIX4による64点FFTの処理を行う関数をリンクします。
SCILABとはフリーの科学技術演算ソフトウエアで、
より入手することができます。
SCILABによるRADIX4 64点FFT : myfft64.sce
以下に英語による簡単なマニュアルをリンクしておきます。 : HowToScilab.pdf
64点FFTのひとつの実装方法として、シフトレジスタを用いるシリアル処理のFFTを説明します。
上記セクションの64FFTの処理アルゴリズムから、3つのステージで処理し、そしてリオーダーが必要なことは理解されたと思います。
STAGE1では、16点ずつ離れた4点から、16点ずつ離れた4点の出力を計算しています。また、STAGE2では4点ずつ離れた4点から、4点ずつ離れた4点の出力を計算し、STAGE3では隣接の4点から隣接の4点を計算します。
このような処理をシフトレジスターを用いた方式で処理することができます。以下の図9はSTAGE3の連続4点のFFT処理を示したものです。左側の正方形はフリップフロップによるシフトレジスタを示しており、計7段のシフトレジスタを構成しています。毎クロックごとにx2入力がシフト入力され、中断の切り替え回路(マルチプレクサ)により、RADIX-4バタフライ回路の入力に4つのx2入力信号が渡されます。RADIX-4バタフライ回路はこの入力に対してステージ3に必要な演算を行います。図中に演算を示していますが、各入力に1、j、−1、−jを乗算して加算を行っています。虚数単位jの乗算は複素数のReal成分とImaginary成分の交換や符号反転で実現できるので、RADIX-4バタフライ回路には乗算は必要なく加算器などで構成されます。最終出力に複素数のTwiddle Factorが複素乗算されていますが、STAGE3では実際にはTwiddel Factorは1なので、乗算の必要はありません。
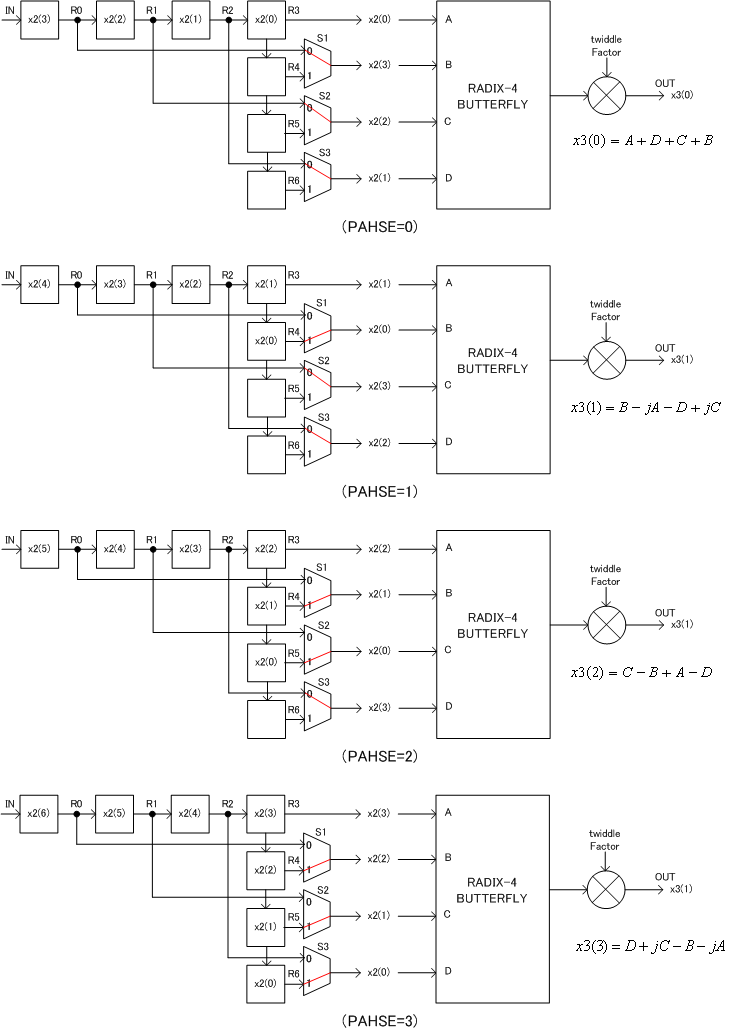
図9 STAGE3 4入力FFTシリアル処理アーキテクチャ
以下図10に図9の動作波形を示します。まず、HEAD信号は’1’で入力の開始を示します。黄色で示される4点が最初のFFT処理すべき入力値です。R0からR6はシフトレジスタの値で、値がシフトしていることがわかります。PHASEはHEAD信号から生成され、S1, S2, S3のスイッチ信号を生成します。結果的に、A, B, C, Dに黄色で示される4点がシフトして現れ、RADIX-4バタフライ回路にて、OUTが計算されます。また、OUT出力の先頭を示すために、OUT_HEADなる信号が示されます。OUT_HEADはHEAD信号をこの処理のレイテンシーのサイクル遅延したものになっています。
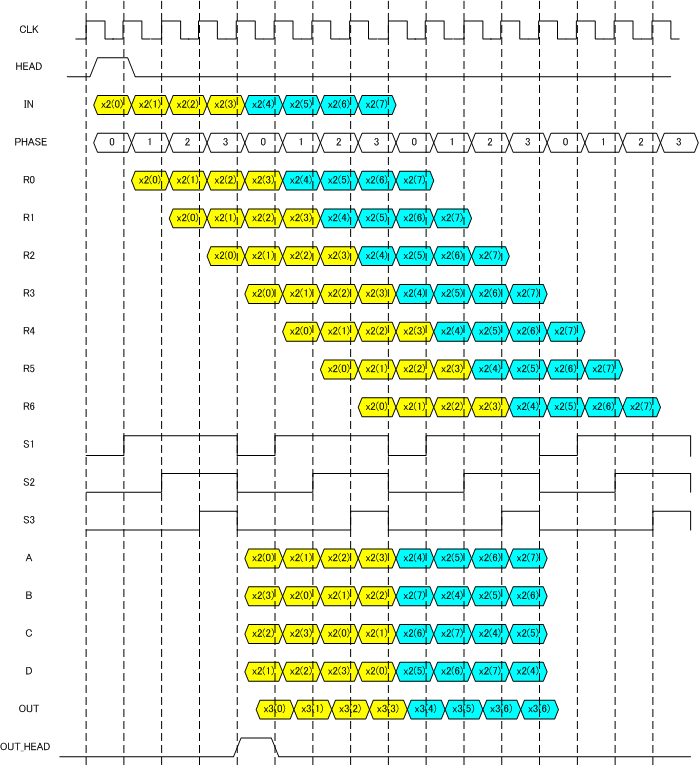
図10 STAGE3 4入力シリアルFFT動作波形
他のステージの処理は、上記STAGE3のシフトレジスタの長さを変更し、やや制御を変更することで実現することができます。また、Twiddle Factorの複素数を生成して、複素乗算することも必要です。以下に参考までに、STAGE2の場合を示しておきます。これから容易にSTAGE1の処理が類推できます。
STAGE2の場合4点おきの入力点を使用するので、シフトレジスタのR0, R1, R2, R3, R4, R5, R6間の段数は4段となります。また、連続の4点を処理している間はPHASE同じであり、4入力点ごとにPHASEをカウントUPします。後は、STAGE3と同じですが、最終段にてTwiddle Factorを乗算します。
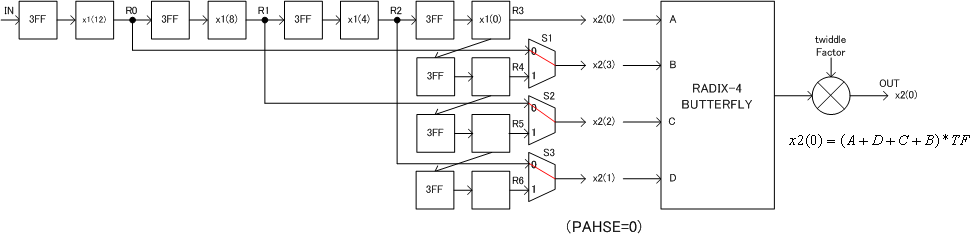
図11 STAGE2 の処理回路
STAGE1では、シフトレジスタのR0, R1, R2, R3, R4, R5, R6間の段数は16段となります。
STAGE3の出力は
![]()
のx3(0), x3(1), x3(2), x3(4), ...の順に出力され、これは本来のFFT出力に変換すると、X(0), X(16), X(32), ...のような出力になります。以下に対応表を示します。このリオーダーを実装するには、FFなどのフリップフロップが必要です。しかしながら、下図表を良く見ると規則性があり、ランダムアクセスメモリやシフトレジスタなどで、リオーダーの実装ができそうなことがわかります。
| x3(k2+4k1+16k0) | X(k0+4k1+16k2) | x3(k2+4k1+16k0) | X(k0+4k1+16k2) | x3(k2+4k1+16k0) | X(k0+4k1+16k2) | x3(k2+4k1+16k0) | X(k0+4k1+16k2) | |||
| 0 | 0 | 16 | 1 | 32 | 2 | 48 | 3 | |||
| 1 | 16 | 17 | 17 | 33 | 18 | 49 | 19 | |||
| 2 | 32 | 18 | 33 | 34 | 34 | 50 | 35 | |||
| 3 | 48 | 19 | 49 | 35 | 50 | 51 | 51 | |||
| 4 | 4 | 20 | 5 | 36 | 6 | 52 | 7 | |||
| 5 | 20 | 21 | 21 | 37 | 22 | 53 | 23 | |||
| 6 | 36 | 22 | 37 | 38 | 38 | 54 | 39 | |||
| 7 | 52 | 23 | 53 | 39 | 54 | 55 | 55 | |||
| 8 | 8 | 24 | 9 | 40 | 10 | 56 | 11 | |||
| 9 | 24 | 25 | 25 | 41 | 26 | 57 | 27 | |||
| 10 | 40 | 26 | 41 | 42 | 42 | 58 | 43 | |||
| 11 | 56 | 27 | 57 | 43 | 58 | 59 | 59 | |||
| 12 | 12 | 28 | 13 | 44 | 14 | 60 | 15 | |||
| 13 | 28 | 29 | 29 | 45 | 30 | 61 | 31 | |||
| 14 | 44 | 30 | 45 | 46 | 46 | 62 | 47 | |||
| 15 | 60 | 31 | 61 | 47 | 62 | 63 | 63 |
今回の課題では0.0625のような小数点以下の数をデジタル回路で取り扱う必要があります。たとえば4ビットの2進数”0111”ですが、小数点をどこの位置に置くかで表す値が変わってきます。たとえば、”01.11”ならば10進数表現では+1.75、”0111.”ならば、10進表現では+7です。
また、4ビットの2進数ですが、それが符号無し数すなわち正または0の数を表しているか、2の補数表現で正または負の数を表しているかを区別する必要があります。”11.10”は符号無し数であれば、10進表現で+3.50となり、2の補数表現であれば、10進表現で-0.50となります。
すなわち、同じ4ビットの2進数でも、「小数点の位置」と「符号無し表現か2の補数表現か」を明確にしないとまったく異なった数に対応してしまいます。
ここではSignal Processing Workbenchで用いられている固定小数点の属性表記方法を解説し、用います。
<8,2,t>
と表記すると、その信号は
8 : 全体のビット数が8ビット
2 : 整数ビットが2ビット
t : two's complement
ということで2の補数表現、すなわち最上位ビットは符号ビットとなる
という意味です。したがって、”01101111”なる8ビットの数の属性が<8,2,t>とすると、
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 符号ビット | 整数部 |
小数部 |
|||||
ということになり、小数部は5ビットとなり、10進表現では+3.46875に対応します。
<8,2,u>
と表記すると、その信号は
8 : 全体のビット数が8ビット
2 : 整数ビットが2ビット
u : unsignedということで、符号無し数すなわち負の数を表さない
という意味です。したがって、同じ8ビットの数”01101111”の属性が<8,2,u>とすると、
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 整数部 | 小数部 | ||||||
ということになり、小数部は6ビットとなり、10進表現では+1.734375に対応します。
整数部のビット数が多いほど表現できる最大数すなわちレンジが大きくなり、小数部のビット数が多いほど表現できる最小数が小さくなり、解像度が向上します。
以下の表1に4ビットの数が<4,2,u>の属性を持つ場合と<4,1,t>の属性を持つ場合の10進表現を示します。
表3 属性による値の違い
4ビットの数 属性<4,2,u>の場合の
10進表現属性<4,1,t>の場合の
10進表現0000 +0.00 +0.00 0001 +0.25 +0.25 0010 +0.50 +0.50 0011 +0.75 +0.75 0100 +1.00 +1.00 0101 +1.25 +1.25 0110 +1.50 +1.50 0111 +1.75 +1.75 1000 +2.00 -2.00 1001 +2.25 -1.75 1010 +2.50 -1.50 1011 +2.75 -1.25 1100 +3.00 -1.00 1101 +3.25 -0.75 1110 +3.50 -0.50 1111 +3.75 -0.25
以下の表2に4ビット長の固定小数点の属性の幾つかの例と、対応する2進数、値のレンジ、解像度を示します。表2からもわかるように同じ4ビット長を用いて多様なレンジと解像度の数値を表現できます。当然のことですが、解像度を悪く大きな値にすると、より広いレンジを表すことができます。
表4 4ビット長の固定小数点の属性の幾つかの例と、対応する2進数、値のレンジ、解像度
属性 2進数表現
Sは符号ビット
Xはデータビットレンジ 解像度 整数 <1,1,u> X. 0 to 1 1 <4,4,u> XXXX. 0 to 15 1 <4,3,t> SXXX. -8 to 7 1 小数 <4,0,u> .XXXX 0.0 to 0.9375 0.0625 (1/16) <4,0,t> S.XXX -1.00 to +0.875 0.125 (1/8) その他 <4,2,u> XX.XX 0.0 to 3.75 0.25 (1/4) <4,2,t> SXX.X -4.0 to + 3.5 0.5 (1/2) <4,5,u> XXXX0. 0 to 30 2 <4,5,t> SXXX00. -32 to 28 4 <4,-1,u> .0XXXX 0.0 to 0.46875 0.03125 (1/32) <4,-1,t> S.SXXX -0.5 to +0.4375 0.0625 (1/16)
複素数は2つの実数をa, bとすると a+jb で複素数を示すことができます。
![]()
であり、虚数単位です。
したがって、2つの複素数 a+jb と c+jd を加算するのは、実数成分と虚数成分のそれぞれの和になりますので、
![]()
となり、2つの実数加算器(通常の加算器)で実現することができます。
(乗算)
2つの複素数 a+jb と c+jd の乗算は以下のようになります。
![]()
したがって、複素乗算は4つの実数乗算と1つの減算と1つの加算で実現できます。
以下に回路構成を図12に示します。複素数a+jbと示しますが、回路の中では2つの信号a, bが存在するだけで、複素加算器は2セットの2つの実数が入力され、それぞれが加算されて、2つの実数を出力する組み合わせ回路であり、複素乗算器も同様です。
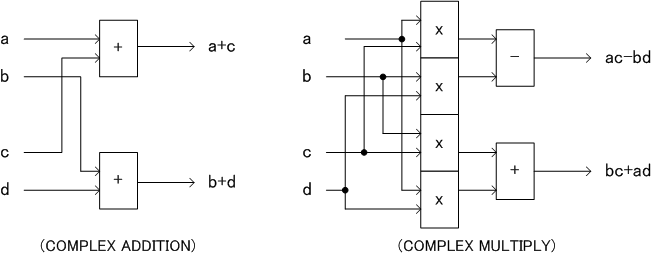
図12 複素演算回路
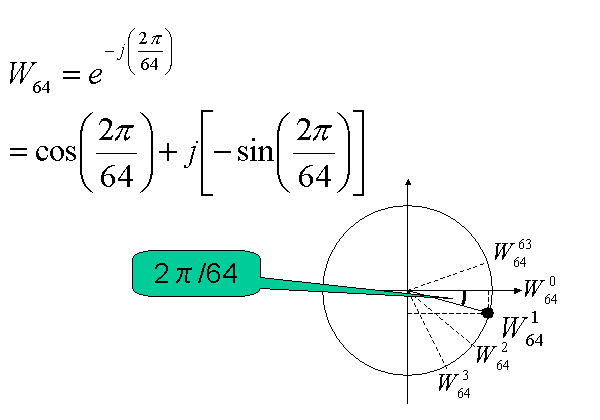
今回以下図13に示されるW64の0乗から63乗までの値がTwiddle Factorとして必要です。Real成分はcos関数で、虚数成分は(-sin)関数ですが、それそれ64種類ですので、アドレスとして6ビットの入力をもつROM2個で実現することができます。
以下に64word X 8bitのROMのデータをリンクします。address=0 〜 63に対応して、一周期分のcosと-sin)の値すなわち、real = cos (2*π*address/64), imag = -sin (2*π*address/64) の10ビットの値が属性<10,0,t>で格納されています。三角関数の値ですので、簡単に生成することもできますが、念のためにリンクしておきます。
基本課題では図14に示すように、シリアルにやってくるFFTINとHEAD信号をもとに、FFT出力FFTOUTとその先頭位置を示すOUTHEAD信号を出力します。図中の太い矢印はFFT計算のレイテンシー(遅延)を示していますが、レイテンシーは任意です。
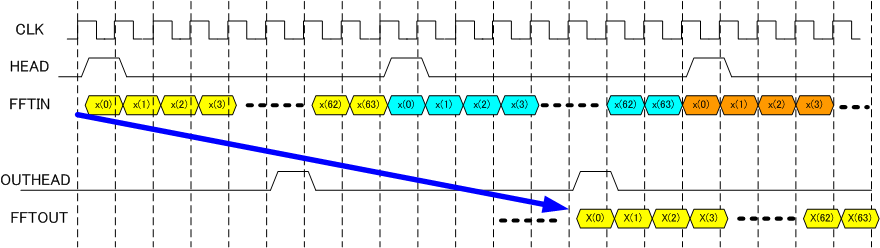
図14 入出力波形
図14のように、64ポイントの入力が休み無く入力され、その先頭位置はHEAD信号で示されます。
表5 基本課題用ピンリスト
|
FFT |
|||
| 信号名 | 入出力 | ビット幅 | 説明 |
| CLK | IN | 1 | クロック入力 |
| HEAD | IN | 1 | ’1’で先頭を示す |
| FFTIN_I | IN | 8 | 入力のREAL成分、<8,0,t>フォーマットとする |
| FFTIN_Q | IN | 8 | 入力のIMAGINARY成分、<8,0,t>フォーマットとする |
| OUTHEAD | OUT | 1 | ’1’で先頭を示す |
| FFTOUT_I | OUT | 14 | 出力のREAL成分、<14,6,t>フォーマットとする |
| FFTOUT_Q | OUT | 14 | 出力のIMAGINARY成分、<14,6,t>フォーマットとする |
以下に、5種類の入力波形とそのFFT結果を例として示します。
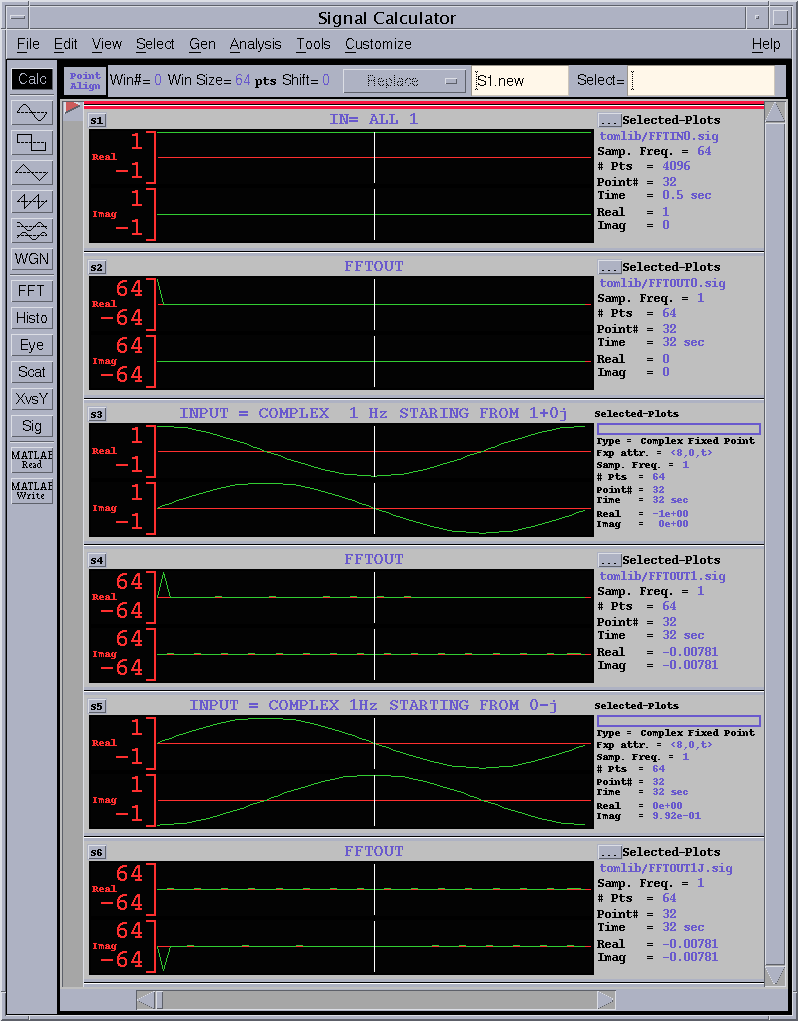
図15 動作波形例(1)
図15の上から1番目の波形は、入力として 1+0j を64点入力した例です。そのFFT出力は2番目の波形であり、INDEX=0番におおよそ64.0の値が出力され、INDEX=2以降は0です。
3番目の波形は、ちょうど1周期の複素回転波形を入力した場合です。FFT出力はINDEX=1に、おおよそ64.0の値が出力されています。回転の初期値が1+0jですので、FFT出力はこの64倍の値になっています。
5番目の波形も、ちょうど1周期の複素回転波形を入力した場合です。ただし、2)とは初期値が異なっています。FFT出力はINDEX=1に、おおよそ-64.0の値が出力されています。回転の初期値が0-1jですので、FFT出力はこの64倍の値になっています。
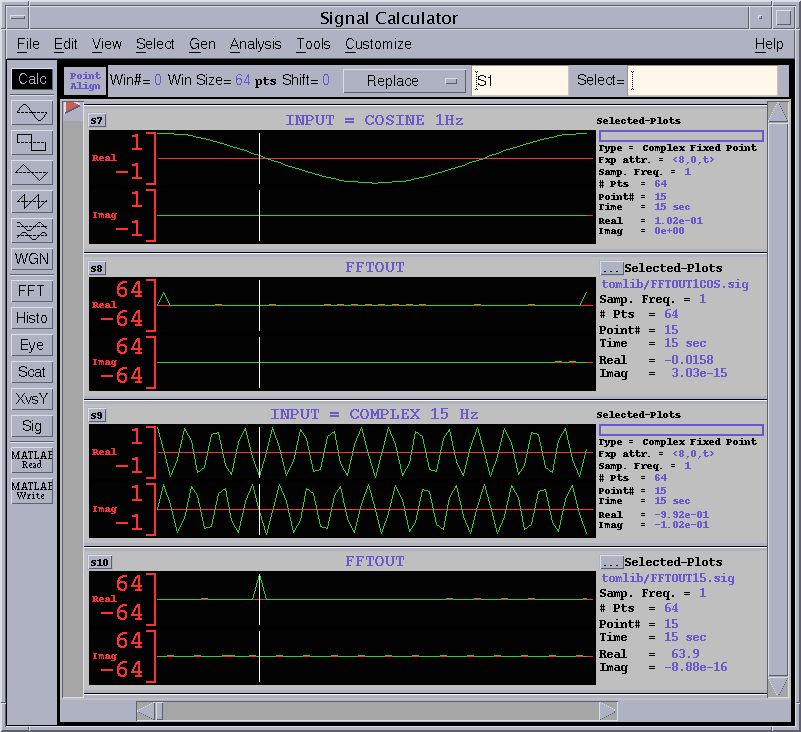
図16 動作波形例(2)
図16の上から1番目の波形は実数のCOS信号で、虚数成分は0です。
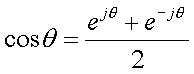
となりますので、1Hzのcos関数は1Hzと-1Hzの成分をもち、それぞれの大きさが0.5である2つの複素の回転の合成と考えることができます。したがって、FFT出力はINDEX=1番とINDEX=63番にこれまでの半分の大きさの32.0の値が出力されています。
FFTでは周期(=64)性より、INDEX=63は-1Hzに対応すると考えることができます。
図16の上から3番目の波形は、ちょうど15周期の複素回転波形を入力した場合です。FFT出力はINDEX=15に、おおよそ64.0の値が出力されています。回転の初期値が1+0jですので、FFT出力はこの64倍の値になっています。
以下に上記5つの入力波形のREAL成分とIMAGINARY成分の値を<8,0,t>フォーマットで以下にリンクします。テスト動作の時に用いてください。
ALL 1 入力: REAL成分 FFTIN0REAL.txt IMAGINARY成分 FFTIN0IMAG.txt
1周期する複素回転信号 初期値=1+0j :REAL成分 FFTIN1REAL.txt IMAGINARY成分 FFTIN1IMAG.txt
1周期する複素回転信号 初期値=0−1j :REAL成分 FFTIN1JREAL.txt IMAGINARY成分 FFTIN1JIMAG.txt
1周期するCOS信号:REAL成分 FFTIN1COSREAL.txt IMAGINARY成分 FFTIN1COSIMAG.txt
15周期する複素回転信号:REAL成分 FFTIN15REAL.txt IMAGINARY成分 FFTIN15IMAG.txt
基本課題では、毎クロックごとに入力信号が与えられていますが、自由課題では、図14の波形などを自由変更してください。
案としては、
クロック周波数をあげて、数クロックごとに1データ入力を行い、クロック周波数の高さを利用して、回路削減をする。
上記例では、シフトレジスタを用いた設計例を示していますが、RAMを用いて設計する。
などです。要は64点FFTを実行するユニークな回路を設計してください。
琉球大学以外からの参加の場合、同一のシノプシスデザインコンパイラの論理合成用ライブラリを使用することが困難であるので、
とします。
具体的には、以下のような多段EXOR回路を例に従って合成し最適化し、その1段あたりの遅延時間を単位時間としてスピードの単位とします。
多段EXOR回路のVHDLソース例:50入力のEXOR回路
この例では6段のEXOR段が合成され、クリティカルパス遅延はreport_timingコマンドにより7.17であったので、7.17/6=1.195を単位(1UNIT_DELAY)とします。
例えば、ある遅延が20ならば、20/1.195=17.74UNIT_DELAYとします。
琉大情報のライブラリ使用者は上記値で換算すればよいです。
また、面積はreport_areaコマンドのtotal cell areaは147.0であり、EXORゲイト数は49個であるので、147.0/49=3.0を単位(1UNIT_AREA)とします。
レポートには以下の内容を含めるてください。また、ページ数を少なめにコンパクトにまとめてください。
| 表紙 | 1 | 代表者の氏名、チーム名、大学院修士/大学学部生/高専生の区別 |
| 2 | 共同設計者全員の名前(最高3名まで)、学籍番号、学年、学校名、住所、電話、email等連絡先 | |
| 3 | 全員のTシャツの希望サイズ(S,M,L,XLのいずれか) | |
| 4 | 取り組んだ課題(LEVEL1/LEVEL2) | |
| 内容 | 1 | 設計した回路ブロックの構成説明(ブロック図と説明) |
| 2 | 設計した回路ブロックの動作説明(動作波形図やパイプライン動作等の説明) | |
| 3 | 工夫した点、オリジナリティを出した点(アピールが重要!) | |
| 4 | クリティカルパスのスピード、論理合成後の回路規模 | |
| 5 | VHDLもしくはVerilogのコード | |
| 6 | 正常動作しているVHDL/Verilogシミュレーション波形 | |
| 7 | その他自由意見など |
レポートはPDFファイルにて下記にEMAILにて提出すること!
他の形式での提出希望あれば、相談してください。
締め切りは2007年1月26日(金)必着です。
本LSI設計コンテストの学生部門の企画・実行、および沖縄での発表会は
主催:LSIコンテスト実行委員会
共催:琉球大学工学部情報工学科、株式会社沖縄産業振興センター、九州半導体イノベーション協議会
協賛: ソニーLSIデザイン株式会社
です。
ENJOY HDL! 沖縄で会いましょう!