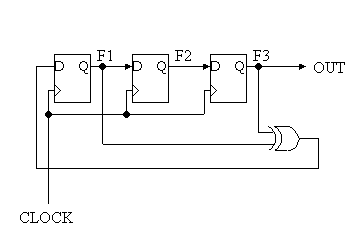
(例題)以下の回路の状態遷移図を完成させよ。但し、各D−FFの初期値はすべて1とする。


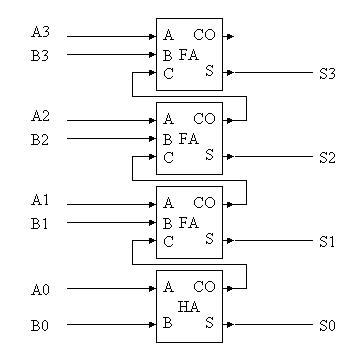
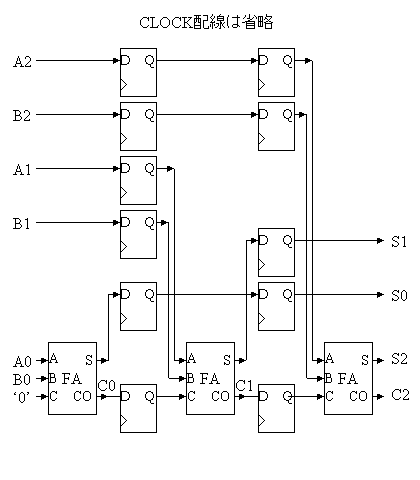
次にこれを以下のように、すべてフルアダーのみで構成する。
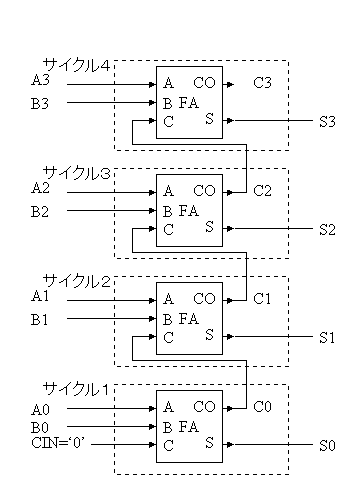
そうすると、各桁ですべて同じ回路が使われていることになる。したがって、この4つのフルアダーを1つにし、1サイクル目でS0,C0を計算し、次サイクルでS1,C1を計算し、3サイクル目でS2,C2を計算し、4サイクル目でS3,C3を計算することが可能である。
ここで、1サイクル目の出力C0を2サイクル目の入力にする必要があります。ここで、D−FFにC0を記憶させる必要があります。
ということで、以下のようにすると、4サイクルで4ビットの加算が可能である。
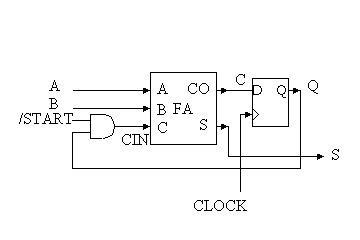
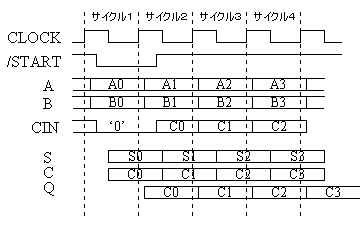
以下の図が動作波形図である。
| サイクル1 | /START=0であるので、CIN=0となり、A0,B0,CIN入力より、S0,C0が計算される。 |
| サイクル2 | /START=1であるので、CIN=C0となり、A1,B1,C0入力より、S1,C1が計算される。 |
| サイクル3 | サイクル2と同様に、A2,B2,C1入力より、S2,C2が計算される。 |
| サイクル4 | サイクル2と同様に、A3,B3,C2入力より、S3,C3が計算される。 |
ちょと複雑であるが、以下のようなことも可能です。
これは3ビットの加算器で、A=(A2,A1,A0)、B=(B2,B1,B0)の2入力を入れた後、
2サイクル後に結果S=(S2,S1,S0)とC2が出力されます。
入力は実は毎サイクル入れてもOKです。以下に動作概念図を示します。

クイズ9 学籍番号 名前 日付 を書いて 提出すること。
1)右下の図は、4ビットの数A=(A3,A2,A1,A0)とB=(B3,B2,B1,B0)からA−Bを計算する減算器である。これを4サイクルで動作する繰り返し型の4ビット減算器に設計変更せよ。
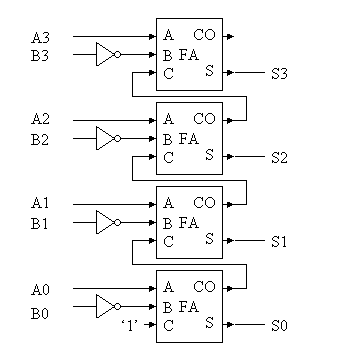
2)上記設計変更した回路の動作波形を示せ。
宿題9 学籍番号 名前 日付 を書いて 提出すること。
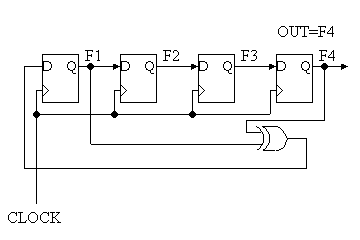
1)下記のリニア・フィードバック・シフト・レジスタの状態遷移図を示せ。全部で何種類の状態が存在するか?
但し、各D−FFの初期値はすべて1とする。
2)フルアダーもしくはハーフアダーを1つと少しの基本ゲートを用いて、4サイクルで動作する繰り返し型の4ビットの2の補数発生器を設計せよ。(ヒント: 2の補数器は以下のようになる。)

以上