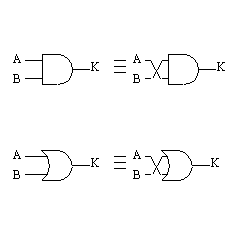
A・B = B・A (1−1)
A+B = B+A (1−2)
1.ブール代数の定義
公理1 可換則 A・B=B・A
A+B=B+A公理2 結合則 A・(B・C) = (A・B)・C
A+(B+C) = (A+B)+C公理3 吸収則 A・(A+B) = A
A+(A・B) = A公理4 分配則 A・(B+C) = (A・B)+(A・C)
A+(B・C) = (A+B)・(A+C)公理5 相補則 最小限φと最大限Iが存在し、任意のAに対し
A・A'=φ
A+A'=I
A'(教科書の表記と異なる)はAの補元
2.ブール代数の公式集
| 1.可換則 | 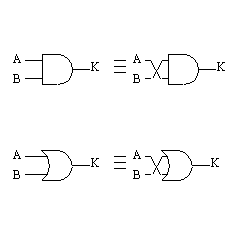 |
|
A・B = B・A (1−1) A+B = B+A (1−2) |
|
2.吸収則 |
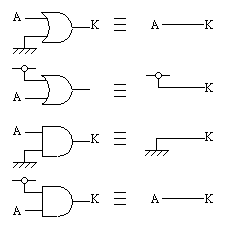 |
|
A+0 = A (1−3) A+1 = 1 (1−4) A・0 = 0 (1−5) A・1 = A (1−6) |
|
3.相補則 |
|
|
A+A' = 1 (1−7) A・A' = 0 (1−8) |
|
4.ニ重否定則 |
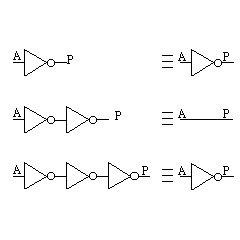 |
|
A'' = A (1−9) NOTゲート2段で、 |
|
5.べき等則 |
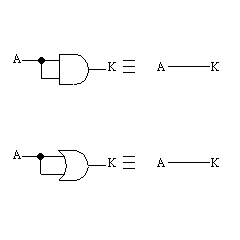 |
|
A・A = A (1−10) A+A = A (1−11) |
|
6.分配則 |
|
|
A・(B+C) = (A・B)+(A・C) (1−12) A+(B・C) = (A+B)・(A+C) (1−13) |
|
7.結合則 |
|
|
A・(B・C) = (A・B)・C (1−14) A+(B+C) = (A+B)+C (1−15) |
|
8.吸収則1 |
AND-OR/OR-ANDで |
|
A・(A+B) = A (1−16) A+(A・B) = A (1−17) A・(A'+B) = A・B (1−18) A+(A'・B) = A+B (1−19) |
|
9.ド・モルガンの定理 |
|
|
(A+B)' = A' ・B' (1−20) (A・B)' = A' + B' (1−21) |
3.例題
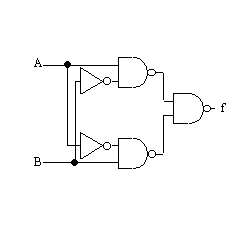
| f = (A+B)・(A・B)' を実現すると | 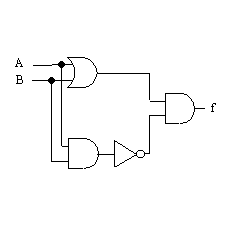 |
トランジスタ数= 6(NOR)+6(AND)+2(NOT)+6(AND) =20 |
|
式を変形する、 f = (A+B)・(A・B)' |
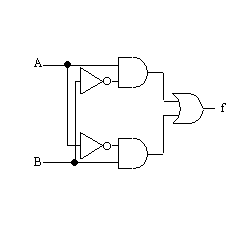 |
トランジスタ数= 6+6+6+2+2 =22 トランジスタ数は増えてしまった! |
|
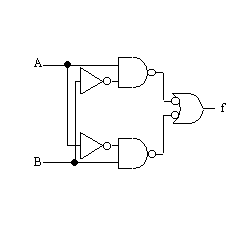
上記回路に対して、NOT2つを挿入 |
ドモルガンの定理適用(16トランジスタで実現) |
 |
 |
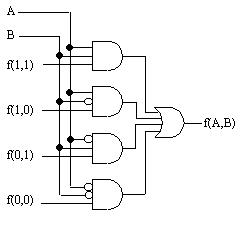
4.シャノンの展開定理
(加法標準形)
f(X1, X2, ..., Xi, ...Xn) = Xi ・ f(X1, X2, ..., Xi-1, 1, Xi+1, ..., Xn) + Xi ' ・ f(X1, X2, ..., Xi-1, 0, Xi+1, ..., Xn)
したがって、
f(A, B) = A・f(1, B) + A'・f(0, B) = A・(B・f(1,1)+B'・f(1,0) ) + A'・(B・f(0,1) +
B'・f(0,0) )
f(A, B) = A・B・f(1,1) + A・B'・f(1,0) + A'・B・f(0,1) +
A'・B'・f(0,0)
|
このような形 (加法標準形:入力信号またはその反転信号をANDし、 に展開することができる。 結果的にf(A,B)=1の項のみ残る。 |
 |
したがって、以下のような真理値表が与えられたら、
| 入力A | 入力B | 出力 f(A, B) |
| 0 | 0 | f(0,0) = 0 |
| 0 | 1 | f(0,1) = 1 |
| 1 | 0 | f(1,0) = 1 |
| 1 | 1 | f(1,1) = 0 |
f(A,B) = A・B・f(1,1) + A・B'・f(1,0) + A'・B・f(0,1) + A'・B'・f(0,0) = A・B' + B'・A
となる。
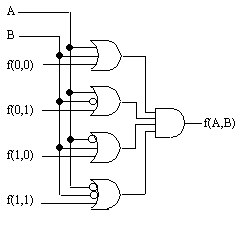
(乗法標準形)
f(X1, X2, ..., Xi, ...Xn) = (Xi + f(X1, X2, ..., Xi-1, 0, Xi+1, ..., Xn) ) ・ (Xi ' + f(X1, X2, ..., Xi-1, 1, Xi+1, ..., Xn) )
f(A,B) = (A+B+f(0,0)) ・ (A+B'+f(0,1)) ・ (A'+B+f(1,0)) ・ (A'+B'+f(1,1))
|
このような形 (乗法標準形:入力信号またはその反転信号をORし、 に展開することができる。 結果的にf(A,B)=0の項のみ残る。 |
 |
クイズ3 学籍番号 名前 日付 を書いて 提出すること。
(注意:回路を設計する場合、特に明記しないが、なるべく少ないゲート数で実現せよ。)
A) 2入力NANDゲートのトランジスタレベルの回路図を書け
B) 2入力ANDの真理値表が書け
C) 2入力ORの真理値表が書け
D) n入力NAND、NORゲートのトランジスタ数はいくらか?
E) n入力AND、ORゲートのトランジスタ数はいくらか?
1) 式 f(A, B, C) = A' ・B・C + A・B'・C + A・B・C' +
A・B・C
をAND、OR、NOTゲート用いて回路図を実現せよ。総トランジスタ数はいくつか?
2)上記式をNAND、NOR、NOTを用いて実現せよ。総トランジスタ数はいくつか?
3)上記式を以下のように変形する。最後の式はどうなる?
f(A, B, C) = A' ・B・C + A・B'・C + A・B・C' + A・B・C
= (A' ・B・C+A・B・C) + (A・B'・C+A・B・C) + (A・B・C' +A・B・C)
=????????????????????
4)上記3)の結果式を、AND、OR、NOTゲートだけを用いて回路図を実現せよ(AND, OR, NOTの全てを用いる必要はない)。総トランジスタ数はいくつか?
5)上記3)の結果式を、NAND、NOR、NOTゲート用いて回路図を実現せよ(NAND, NOR, NOTの全てを用いる必要はない)。総トランジスタ数はいくつか?
宿題3 学籍番号 名前 日付 を書いて 提出すること。
(注意:回路を設計する場合、特に明記しないが、なるべく少ないゲート数で実現せよ。)
1) A・C + B・C' + A・B = A・C + B・C' をブール代数の公式を用いて、証明せよ。
(左辺を変形してゆき、右辺にする)
2) 以下の真理値表で与えられる論理関数を乗法標準形で表せ。
| 入力A | 入力B | 出力 f(A, B) |
| 0 | 0 | f(0,0) = 0 |
| 0 | 1 | f(0,1) = 1 |
| 1 | 0 | f(1,0) = 1 |
| 1 | 1 | f(1,1) = 0 |
3) 上記2)の乗法標準形をAND、OR、NOTゲートを用いて回路図を実現せよ(AND, OR, NOTの全てを用いる必要はない)。総トランジスタ数はいくつか?
4) 上記2)の乗法標準形をNAND、NOR、NOTゲートを用いて回路図を実現せよ(NAND, NOR, NOTの全てを用いる必要はない)。総トランジスタ数はいくつか?
5) 以下の真理値表で与えられる回路をNAND、NOR、NOTだけを用いて設計せよ(NAND, NOR,
NOTの全てを用いる必要はない)。
(ヒント:この回路は加算器で、3つの入力の1の数を数えて、2桁の2進数(上位:C、下位:S)として出力する回路)
それぞれの出力Cと出力Sに関する論理式を加法標準形で求めて、回路図を作成すればよい。
2つの回路で同じ信号を共通に使用してもよい。
| 入力A | 入力B | 入力C | 出力C | 出力S | |
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | 1 | |
| 0 | 1 | 0 | 0 | 1 | |
| 0 | 1 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 1 | 0 | |
| 1 | 1 | 0 | 1 | 0 | |
| 1 | 1 | 1 | 1 | 1 |
6) 上記5)で設計した回路の総トランジスタ数はいくらか?
以上