状態遷移マシン
簡単な順序回路の例
- 以下の図はD-FF 2個とEXOR(排他的論理和)ゲートからなる順序回路である。
- 回路の内部の状態はDフリップフロップに記憶される。
- このDフリップフロップの値は入力データDINがシフトしてきたものであり、状態の遷移の方法は最も単純である。
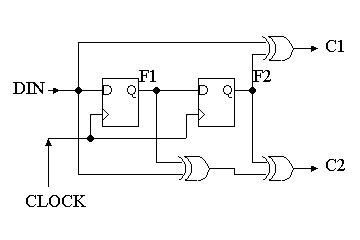
- 2入力EXORゲートは半加算器にも使用されるゲートであり、入力の2つのビットを加算して、その結果を2で割ったあまりに対応する。
- 真理値表を書くと以下のようになる。
| 入力 |
|
出力 |
| 入力A |
入力B |
|
EXORゲートの出力 |
| 0 |
0 |
|
0 |
| 0 |
1 |
|
1 |
| 1 |
0 |
|
1 |
| 1 |
1 |
|
0 |
- この順序回路のデータ入力端子DINに 0,1,0,0,1,1の順にCLOCKに同期して以下の図のようにデータを入力すると、1段目のD-FFの出力F1と、2段目のD-FFの出力F2は以下のように変化する。
- 回路から明らかなように、F1は入力データを1サイクル遅らせたものになり、F2はF1を1サイクル遅らせたものとなる。
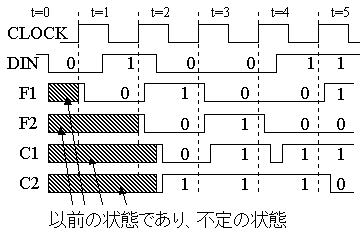
- C1、C2はDIN、F1、F2からEXORでそれぞれ計算される。
ここで注目すべきことは、
- 回路には2つのD-FFがあり、F1とF2はそれぞれ’0’もしくは’1’の値を保持するので、組み合せれば計4種類の状態を持つことになる。
- 図のt=2とt=3のサイクルでは同一の入力データ’0’が入力されているが、出力(C1,C2)=(0,1)と(1,1)であり、入力データが同じでも出力データは異なる。これが、組み合せ回路との相違である。
状態遷移表
- 先ほどのt=2の時に(F1,F2)=(1,0)であり、その時にDIN=0を入力したので、(C1,C2)=(0,1)となる。
- また、t=3の時には、(F1,F2)=(0,1)である。
- ということでこのような関係を表に書くことができる。
| t=nの時の状態 |
t=n+1の時の状態F1、F2 |
t=nの時の出力C1,C2 |
| F1 |
F2 |
入力DIN |
入力DIN |
| 0 |
1 |
0 |
1 |
| 0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
| 0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
| 1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
| 1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
- ここで、t=nの時の状態を示しているが、t=nの時とはt=nのサイクルで値等がすべて安定した時の値であり(t=nサイクルの後半の方の値)これはすなわち、t=n+1になる時のクロックの立ち上がりの瞬間の値を言う。(これは重要です。)
状態遷移図
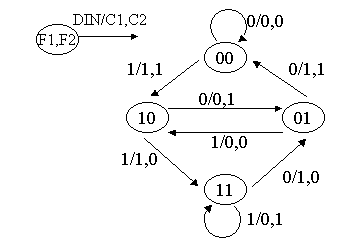
- また、状態遷移表を以下のような状態遷移図を用いて表すこともできる。
- ここで、○は状態を表し、4つの状態があることがわかる。
- また、矢印で各入力データに対する状態の遷移を示す。
- その時に、出力データ矢印の横に示されている。
同期式4ビットカウンタの設計
- 4ビットすなわち、"0000", "0001", "0010", ..., "1111", "0000",
... と言うように数字を数えるカウンタを設計する。
- 10進法で示すと、0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 0, 1,
...のように数える。
- カウンターは単純な機能であるが、マイクロプロセッサのプログラムカウンタや、パソコンのメインメモリのリフレッシュカウンター等、色々なところに用いられている。
- プログラムカウンタとは、実行すべき命令のアドレスを示すカウンタ
- パソコンのメインメモリに使われているDRAM(ディーラム)は、定期的に内容を書き直さないとデータが消えてしまう。リフレッシュカウンタは、この定期的なデータの書き直し(リフレッシュ)を指示する。
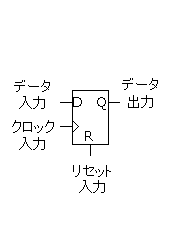
(1)今回、初期値を設定するためにリセット(RESET)端子付D-FFを用いる。
| リセット付D−FFシンボル |
リセット付D−FFの動作波形 |
 |
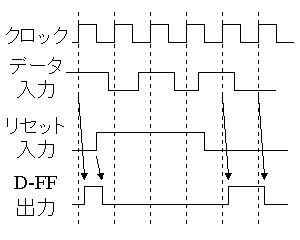 |
- リセット入力がHIGHであれば、クロックに関係なく、データ出力は’0’となる。
(2)4ビットの値を保持する必要があるので、リセット付D−FFを4つ用いる。下図のように、それぞれのD−FFは2進数の各桁に対応する。リセットを’1’にすれば、4つのD−FFの出力は’0’となるので、"0000"からカウントすることができる。
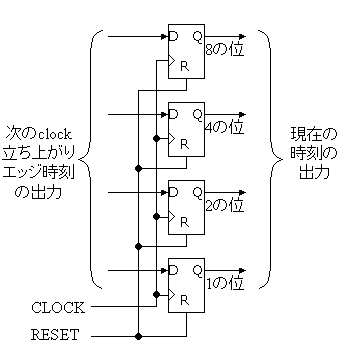
(2)ある時刻に4つのリセット付D−FFにある値が入っているとすると、次の時刻にD−FFの値は前の値+1になればよい。これは、D−FFの4つの入力が現在の出力+1になればよいことを示す。
- +1をつくる回路を特に、インクリメンタという。以下に4ビット加算器と、4ビットのインクリメンタを示す。
| 4ビット加算器 |
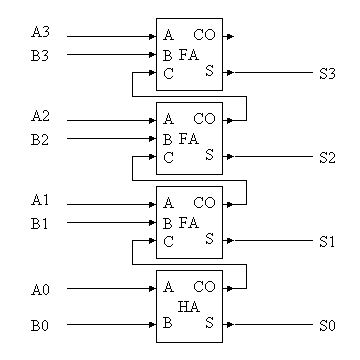 |
| 4ビットインクリメンタ |
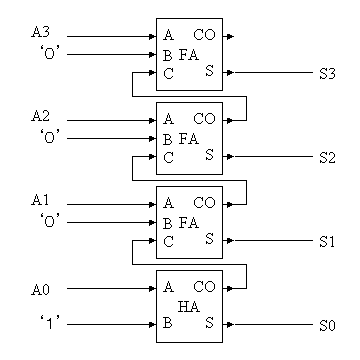 |
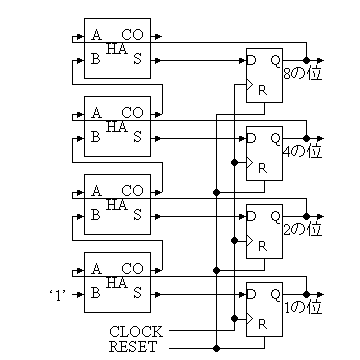
(3)結果的に、4ビットカウンタは以下のようになる。’0’が入力されるフルアダーはハーフアダーで実現できるので、FAをHAに変更してます。
宿題6 学籍番号 名前 日付 を書いて 提出すること。
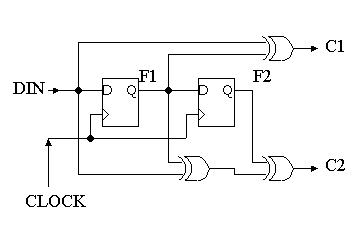
1) 以下の回路図の状態遷移図を描け
2) 10進数で示すと、0,3,6,9,12,15,2,5,8,11,14,1,4,7,10,13,0、なる順で3ずつ上昇する4ビットカウンターを設計せよ。
3) 以下の回路図の状態遷移図を描け
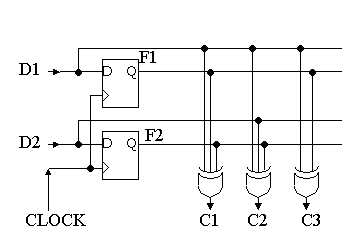
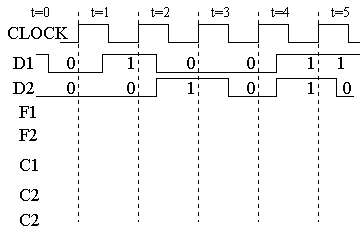
4) 同じ回路に以下の図に示されるD1,D2波形を入力した時のF1,F2,C1,C2,C3の波形を描け!
但し、F1,F2の初期値はともに’0’とする。
5) 10進数で示すと、0,15,14,13,12,11、10,9,8,7,6,5,4,3,2,1,0、のように1ずつ値が現減少する4ビットのカウンタを設計せよ。
今回示した、単純な順序回路は実は携帯電話や衛星TV放送などのデジタル通信での、伝送エラーを訂正するために用いられている「畳み込み符号器」です。
以上












