(1)
f=(A+B)・(A・B)' = A・B' + A'・B を証明する。
前回説明した公理や公式をもちいる。
| f=(A+B)・(A・B)' | |
| ドモルガンの定理を適用すると | =(A+B)・(A'+B') |
| 分配則で展開すると | =A・(A'+B') + B・(A'+B') |
| さらに、分配則で展開すると | =A・A' + A・B' + B・A' + B・B' |
| 相補則で変形すると、 | =0 + A・B' + B・A' + 0 |
| 吸収則により’0’は消えるので | =A・B' + B・A' |
(2)
A + A'・B = A + B を証明する。
| A + A'・B | |
| 吸収則でAをA・1と考える | = A・1 + A'・B |
| 相補則により1=B+B'と考える | = A・(B+B') + A'・B |
| 分配則により展開する | = A・B + A・B' + A'・B |
| べき等則によりA・Bを2項にする | = A・B + A・B + A・B' + A'・B |
| 可換則により計算順序をかえる | = (A・B+A・B') + (A・B+A'・B) |
| 分配則で因数分解すると | =A・(B+B') + B・(A+A') |
| 相補則により | =A・1 + B・1 |
| 吸収則により | =A + B |
以下の真理値表から加法標準形のブール式の作り方。
| 入力A | 入力B | 入力C | 出力f | |
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 1 | |
| 0 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 0 | |
| 1 | 1 | 0 | 0 | |
| 1 | 1 | 1 | 1 |
f = A'・B'・C + A'・B・C' + A・B'・C' + A・B・C
となる。
f = (A+B+C)・(A+B'+C')・(A'+B+C')・(A'+B'+C)
となる。
これを展開すると、ちゃんと f = A'・B'・C + A'・B・C' + A・B'・C' + A・B・C になります。
カルノー図による論理関数の簡単化
| ORの真理値表 | ||
| 入力A | 入力B | 出力f(A、B) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
f = A'・B + A・B' + A・B Aでくくると、 =A・(B+B') + A'・B 相補則により、 =A + A'・B うまくORの形にならない。 再度挑戦 f = A'・B + A・B' + A・B べき等則 = A'・B + A・B' + A・B + A・B = (A・B+A'・B) + (A・B+A・B') 分配則で因数分解すると、 =(A+A')・B + A・(B+B') =B+A
そこでカルノー図を用いて式の簡単化をする。
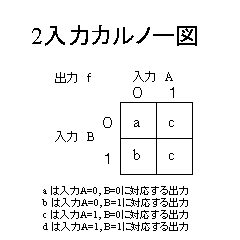
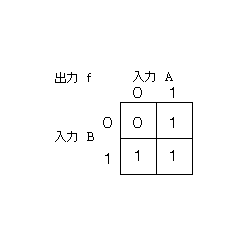
| 2変数のカルノー図 | 2入力ORのカルノー図 | |||
 |
 | |||
| 2入力ORのカルノー図 | 2入力ORのカルノー図 |
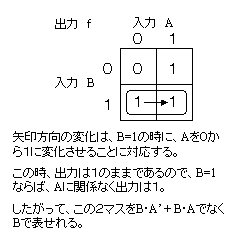 |
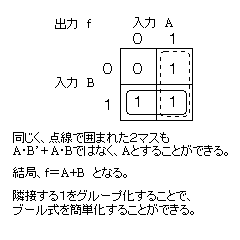 |
3入力のカルノー図
| 3変数のカルノー図 |
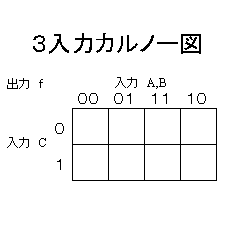 |
(注意:回路を設計する場合、特に明記しないが、なるべく少ないゲート数で実現せよ。)
1) A・(A' + B) = A・B をブール代数の性質をもちいて証明せよ。
(ヒント:これはめちゃ簡単!)
2) (A・B + A'・B')' = A・B' + A'・B をブール代数の性質をもちいて証明せよ。
(ヒント:ドモルガンの定理を用いる)
3)以下の真理値表をカルノー図で表し、隣接する1があれば○で囲み、その結果より出力関数fのブール式を求めよ。
| ???の真理値表 | ||
| 入力A | 入力B | 出力f(A、B) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
以上