カルノー図の続きと基本機能ブロック

カルノー図による論理関数の簡単化（続き）

４入力のカルノー図

４変数のカルノー図

例題

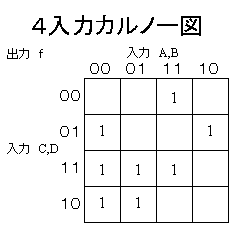
f(A,B,C,D) = A･B･C'･D' + A'･B'･C'･D + A･B'･C'･D + A'･B'･C･D +
A'･B･C･D + A･B･C･D + A'･B'･C･D' + A'･B･C･D'

を簡単化する。以前やった、ブール式の性質だけでは難しそうでが、
カルノー図でやると以下のようになります。

４変数のカルノー図	隣接する2n個（１,２,４、...） の’１’をグループ化する

• 四角で囲った部分はANDゲートとなり、全体をORすることになる。
• オーバーラップしてでも、四角で多くの１を囲む方が良い、
  １の数が１つでは４入力ANDゲート、２つでは３入力ANDゲート、
  ４つでは２入力ANDゲートとゲートが単純（トランジスタ数が少ない）になる。
• 点線の四角の囲みはなくても、すべての１を囲めているので、不要である。

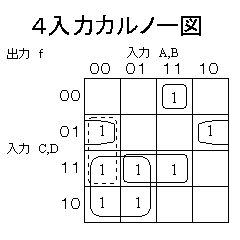ということで、

f(A,B,C,D) = A･B･C'･D' + B'･C'･D + A'･C + B･C･D

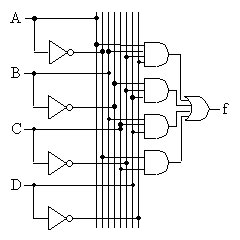
と簡単化される。回路図は以下のようになる。

簡単化したあとの回路図	NAND,NOR,NOTを使って トランジスタ数を減らすと、
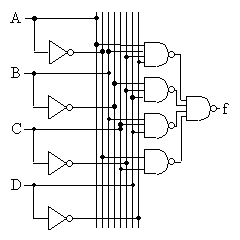トランジスタ数は 2*4 + 10 + 2*8 + 6 + 10 = 50	トランジスタ数は 2*4 + 8 + 2*6 + 4 + 8 = 40

禁止項を利用した簡単化

• まず、禁止項とはなにか？
  --> そのような入力の組み合わせが発生せず、出力がどうでもよい。
• 英語では　DON'T　CARE　（ドントケア）と言い、「気にしない、どうでも良い」の意味

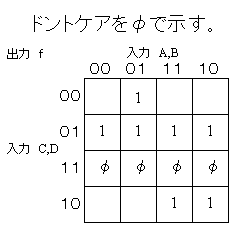
例題

４変数のカルノー図	隣接する2n個（１,２,４、...） の’１’をグループ化する

• ドントケア（φの部分）はそのような入力はされなくて、そのときの出力はどうでもよいので、必要であればそれを１と考えることで、四角で囲まれたグループを大きくする。
• 説明したように、囲みが大きいほど、対応するANDゲートの入力数は減り、トランジスタ数が減る。
• 一般的に、トランジスタ数が少ない方が、LSI上の面積が小さく、かつ動作スピードも速い。
• もちろん、すべてのドントケアを囲む必要はない。

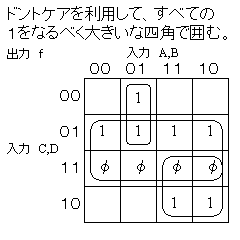ということで、f(A,B,C,D) = A'･B･C' + D + A･C

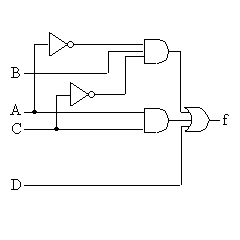
と簡単化される。回路図は以下のようになる。

簡単化したあとの回路図	NAND,NOR,NOTを使って トランジスタ数を減らすと、
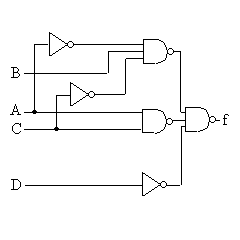トランジスタ数は 2*2 + 8 + 6 + 8 = 26	トランジスタ数は 3*2 + 6 + 4 + 6 = 22

基本的な組み合わせ回路

• 今まで、組み合わせ回路の設計方法を見てきたが、ここでは代表的な組み合わせ回路をみる。

（１）半加算器（教科書４．４．１）

• １ビットの数２つを加算する回路。

半加算器の真理値表					半加算器のシンボル
入力A	入力B		桁上がり 出力CO	和 出力S
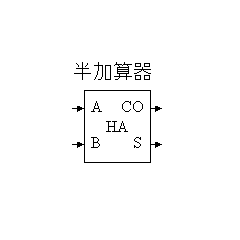０	０		０	０
０	１		０	１
１	０		０	１
１	１		１	０

（２）全加算器

• 多ビットの２進数の加算を行う場合、２つの１ビットの加算の他に、下位のビット加算で生じた桁上がりの加算も行う必要がある。したがって、１ビットの数３つを加算する必要があり、これを全加算器という。

全加算器の真理値表						全加算器のシンボル
入力A	入力B	入力C		桁上がり 出力CO	和 出力S
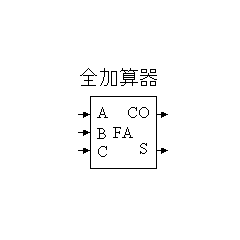０	０	０		０	０
０	０	１		０	１
０	１	０		０	１
０	１	１		１	０
１	０	０		０	１
１	０	１		１	０
１	１	０		１	０
１	１	１		１	１

（３）マルチプレクサ

• 複数の入力から１つをえらぶ回路

選択制御信号Sが’０’でAを出力、’１’でBを出力

２入力１出力マルチプレクサの真理値表					２入力１出力マルチプレクサのシンボル
入力S	入力A	入力B		出力Y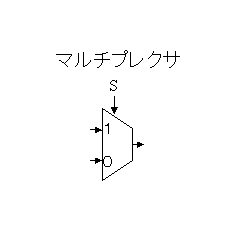
０	０	０		０
０	０	１		０
０	１	０		１
０	１	１		１
１	０	０		０
１	０	１		１
１	１	０		０
１	１	１		１

（４）デマルチプレクサ

• １つの入力を複数の出力へ振り分ける回路

選択制御信号Sが’０’で入力をXに出力、’１’で入力をYに出力

１入力２出力デマルチプレクサの真理値表					１入力２出力デマルチプレクサのシンボル
入力S	入力A		出力X	出力Y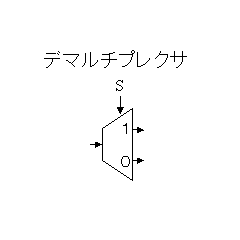
０	０		０	０
０	１		１	０
１	０		０	０
１	１		０	１

HW-5　　学籍番号　名前　日付　を書いて　提出すること。

１）以下をカルノー図を用いてブール式を簡単化せよ。

f = A'･B'･C'･D' + A'･B･C'･D + A･B･C･D + A･B'･C'･D
+ A'･B'･C･D' + A･B･C'･D + A'･B･C･D + A･B'･C･D

２）前問でA'･Dが禁止項の場合、ｆはどのように簡単化されるか示せ。

３）上記２）の論理関数ｆを回路図を実現せよ。（なるべく少ないトランジスタ数で実現せよ。）
また、そのときのトランジスタ数はいくつか？

４）二つの２ビットの２進数A、Bがあるとき、
(i) A>Bのとき、出力が１となる論理関数ｆの真理値表を描け
(ii)　(i)で得られた真理値表より加法標準形で論理関数を表せ
(iii) (ii)の論理関数について、カルノー図を描き簡単化を行え。
(vi) 簡単化された論理関数を実現せよ。
この時、２進数AのMSBをA1、LSBをA0、BのMSBをB1、LSBをB0とせよ。

５）上記１）の論理関数の回路図をなるべく少ないトランジスタ数で実現せよ。
また、そのときのトランジスタ数はいくつか？

６）上記４）でA=Bの時だけ、出力が１となる回路を同様の手順で設計せよ。
この時、２進数AのMSBをA1、LSBをA0、BのMSBをB1、LSBをB0とせよ。

７）講義で示した２入力１出力マルチプレクサをなるべく少ないトランジスタ数で回路を実現せよ。
また、そのときのトランジスタ数はいくつか？

８）半加算器と全加算器を用いて、４ビットの数A=(A3,A2,A1,A0)、B=(B3,B2,B1,B0)の加算器を設計せよ。
半加算器と全加算器として、下記のシンボルをもちいよ。

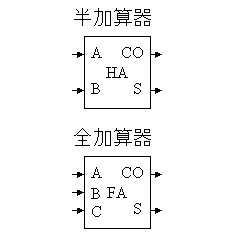
以上