状態遷移マシン（２）

宿題５のD-FFによる状態遷移マシンの復習

（１）

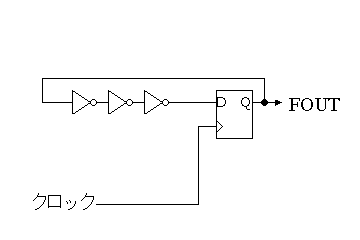
宿題５−１のＦＦ部分の回路図
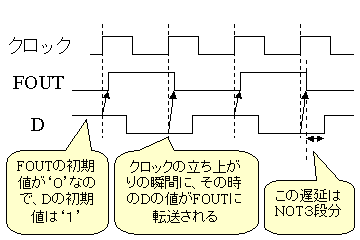
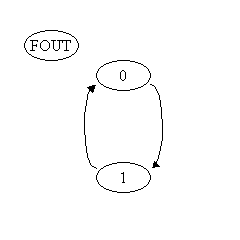
動作波形図	状態遷移図

（２）

宿題５−２の回路図
動作波形図

以下の内容が重要！！！

• ＦＦの出力はクロックの立ち上がりエッジのみで変化する。
• ＦＦの出力と外部からの入力信号で、ＦＦの入力信号Ｄが決まる。
• 次のクロックエッジで、そのＤが新たなD-ＦＦの出力となる。
• 状態遷移図の状態とはＦＦの出力の値の組み合せである。

Ｄフリップフロップを用いて状態遷移マシンを設計する
（ディジタル回路の後半の講義で最も重要な内容）

(例題１）整数で書いて、０、１、２、３、４、５、０、１、２、３、４、５、と０から５を繰り返すカウンタを設計する。
実際には、２進法で"000", "001","010", "011", "100", "101"を繰り返すようにする、ＲＥＳＥＴ信号で"000"に戻せるようにする。

（ＳＴＥＰ１）　"000", "001","010", "011", "100", "101"　なる６つの状態をもつ必要があるので、３つのDフリップフロップが必要である。また、ＲＥＳＥＴ信号が’１’の時に、３つのＤ−ＦＦの出力を’０’にする必要があるので、ＲＥＳＥＴ付のＤ−ＦＦを用いると、以下のようになりそう。

（ＳＴＥＰ２）　上記回路では、ＣＬＯＣＫの立ち上がりエッジにてD0はQ0へ、D1はQ1へ、D2はQ2へ転送される。

したがって、組み合せ回路は入力Q0, Q1, Q2から次の状態を作り出し、それをD0, D1, D2へ出力すれば良い。

したがって、以下の真理値表に示される組み合せ回路を設計すれば良い。’Ｘ’はＤＯＮ’Ｔ　ＣＡＲＥです。

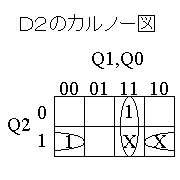
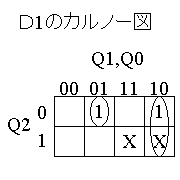
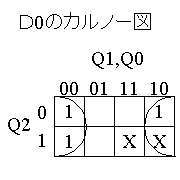
（ＳＴＥＰ３）　上記真理値表からカルノー図を作成して、組み合せ回路を設計する。

Ｄ２のカルノー図	Ｄ１のカルノー図	Ｄ０のカルノー図

• ということで、簡単化されたブール式は

D2 = Q1･Q0 + Q2･Q0'

D1 = Q1･Q0' + Q2'･Q1'･Q0

D0 = Q0'

• したがって、組み合せ回路は以下のようになる

もし、Ｄ−ＦＦの出力が整数で６="110"や７="111"になったらどうなるのか？

• Ｑ２＝１，Ｑ１＝１，Ｑ０＝０の時、組み合せ回路出力Ｄ２＝１、Ｄ１＝１、Ｄ０＝１となるので、
• ６の次は７になる。
• Ｑ２＝１，Ｑ１＝１，Ｑ０＝１の時、組み合せ回路出力Ｄ２＝１、Ｄ１＝０、Ｄ０＝０となるので、
• ７の次は４になる。

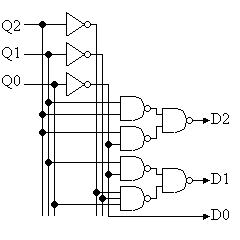
すなわち、もし雷等のノイズでＤ−ＦＦの出力が整数値で６になると、以下のように動作する。

６　⇒　７　⇒　４　⇒　５　⇒　０　⇒　１　⇒　２　⇒　３　⇒　４　⇒　５　⇒　０

• もし上記真理値表で、’Ｘ’をすべて’０’で設計すれば、

６　⇒　０　⇒　１　⇒　２　⇒　

もしくは

７　⇒　０　⇒　１　⇒　２　⇒　

となるように設計できる。

雷などのノイズを考えれば、ＤＯＮ’Ｔ　ＣＡＲＥ　を使わない設計も重要である。

クイズ８　　学籍番号　名前　日付　を書いて　提出すること。

１）整数で書いて、０、１、２、３、４、０、１、２、３、４、と０から４を繰り返すカウンタを設計する。
実際には、２進法で"000", "001","010", "011", "100", "000"を繰り返すようにする、ＲＥＳＥＴ信号で"000"に戻せるようにする。DONT' CAREを用いて、設計せよ。

宿題７　　学籍番号　名前　日付　を書いて　提出すること。

１）整数で書いて、０、５、４、３、２、１、０、５、４、３、２、１、０と繰り返すカウンタを設計する。
実際には、２進法で"000", "101","100", "011", "010", "001", "000"を繰り返すようにする、ＲＥＳＥＴ信号で"000"に戻せるようにする。例題と同様にＤＯＮ'T CAREを利用して、回路を小さくすること。

２）上記カウンタでは３ビットのＤ−ＦＦを用いたので、Ｄ−ＦＦの出力が、整数で、６，７になることはないが、実際の電子機器では雷等のノイズで、Ｄ−ＦＦの出力が６，７に誤動作で変化することがある。
このようなノイズに対応するために、Ｄ−ＦＦの出力が整数で、６もしくは７になっても、次のサイクルで０に変化し、以下のように動作するように設計し直せ。

• ６⇒０⇒５⇒４⇒３⇒２⇒１⇒０⇒５⇒４⇒３
• ７⇒０⇒５⇒４⇒３⇒２⇒１⇒０⇒５⇒４⇒３

以上