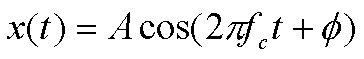
4−1 コンスタレーション (星座のことですが。。。)
変調の3つのパラメータ:
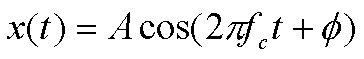
(1)振幅:A
(2)周波数: fc (Hz) 周期: Tc=1/fc (s)
(3)位相ずれ: Φ
の内の2つ(1)と(3)を2次元平面状の点であらわす。
図4−1
X軸からの角度が位相、原点からの距離が振幅
「クイズ1」 BPSKとQPSKのコンスタレーションはどうなるか?
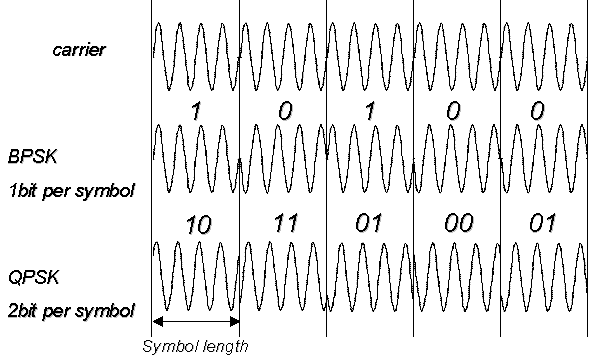
「クイズ2」I相(In Phase)の波とQ相(Quadrature Phase)の波とはなにか? (P79)
波の直交とは
EVMとは
ここからは教科書に無い補足事項
無線信号処理では、三角関数の代わりに以下の
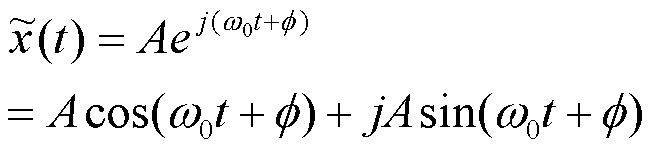
複素指数関数を使用する。
〇これは、I軸を実数、Q軸を虚数とする平面での回転を示す関数となる。 (回転関数)
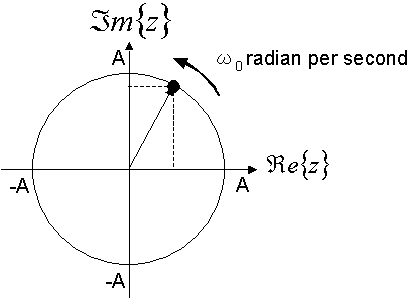
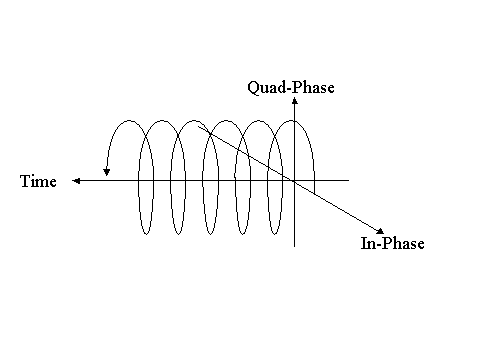
〇無線信号処理では、三角関数x(t)のかわりに、x(t)を使って処理をする。これを解析的信号とよぶ。
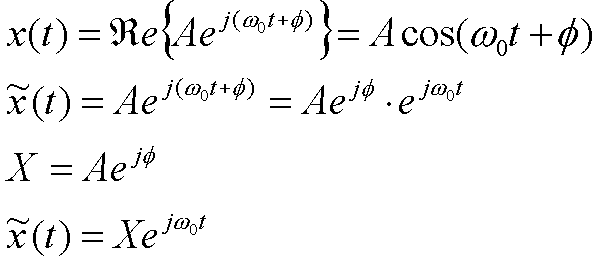
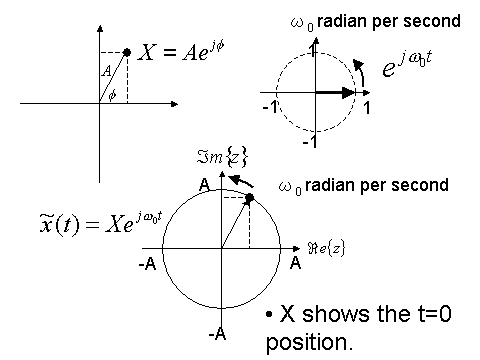
〇この複素指数関数のX(複素振幅という)は振幅と位相を示すもので、上記コンスタレーションと同じものである。
宿題3
(1)キャリア周波数が1KHzとして、以下の図のコンステレーションA,B,Cで示されるように変調された波を図示せよ!
図は、キャリア波形、と変調波形を2段で図示し、第1シンボルがA、第2シンボルはB、第3シンボルはCとせよ。
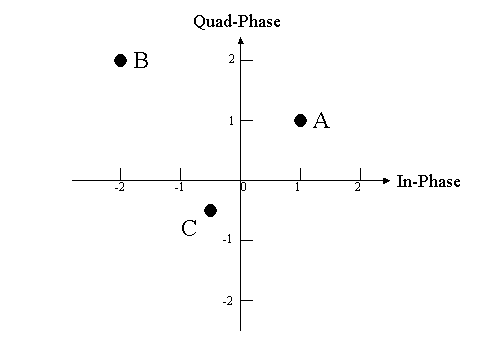
(2)上記A,B,CのコンスタレーションからEVM=50%となる軌跡を図示せよ。
(3)解析的信号は複素数であり、虚数成分を含むが、その実部をとれば実数信号で、私たちが扱う波となる。
解析的信号x(t)が与えられた時にRe[]演算をすればよいのだが、実際にはどのように計算すればよいか?
以上