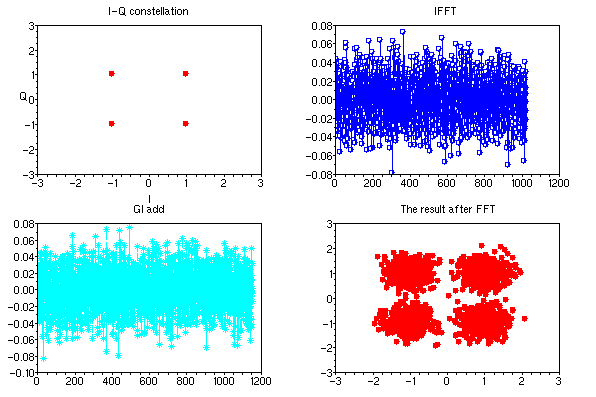
以下にあるノイズを与えた時のシンボルエラーレイトを測定するOFDM通信システムシミュレーションのSCILABコードを示す。
コードのリンク: qpsk_ofdm1.sce
| //Program: //Simple OFDM system //Fire Wada Lab // //Usage: //Execute-> Load into Scilab (or Ctrl L) clear; num_symbol = 2 ; // number of symbols num_point = 1024; // points in symbol M = 4; // size of signal constellation modqpsk= [1+%i, -1+%i, 1-%i, -1-%i]; //1 . create random data rand("uniform"); data = floor(rand(num_point,num_symbol)*M); //data = [0 1 2 3]; |
clear により以前の状況をクリアする。
modqpsk(1)=1+%i を設定し、後ほどデータ値からコンスタレーションへの変換に用いる。
[0..1)の一様乱数を使用する。一様uniform 1024*2個の0から3の整数をデータとして生成する。 |
| //2. mapping into I-Q constellation data_1 = matrix(modqpsk(1+data),num_point,num_symbol); subplot(2,2,1); a = get("current_axes"); a.data_bounds = [-3,-3;3,3]; xtitle("I-Q constellation","I", "Q"); plot(real(data_1),imag(data_1),'r.'); |
dataを1024*2の行列の形で、コンスタレーション値に対応させる。
コンスタレーションをPLOTする。 |
| //serial to parallel data_2 = data_1; //3. IFFT data_3 = ifft(data_2); subplot(2,2,2); a = get("current_axes"); xtitle("IFFT"); plot((real(data_3)),'ob-'); //4. GI add data_4 = [data_3(897:1024,:);data_3] ; |
IFFTを実行してOFDM波形とする。
波形をプロットする。ここでは、複素数なので、実成分のみPLOTしている。 ガードインターバルを追加する。 |
| //4.1 Add Noise sigpower=mean(abs(data_4).^2); sn= 10; // 10dB rand("normal"); awgn = (rand(num_point+128,num_symbol)+%i*rand(num_point+128,num_symbol)); awgnpower=mean(abs(awgn).^2); awgn = awgn/sqrt(awgnpower)*10^(-sn/20)*sqrt(sigpower); data_4=data_4+awgn; subplot(2,2,3); a = get("current_axes"); xtitle("GI add"); plot(real(data_4),'*cya--'); |
信号のパワーを計測する。 sigpower 正規分布の乱数を用いて、ノイズ信号を発生する。 ベースバンド処理であり、ノイズの複素数である。 ノイズパワーを計測する。awgnpower sn比に応じてノイズ信号振幅を調整する。 ノイズを信号に加算する。
|
| //5. GI remove data_5 = data_4(129:1152,:); //6. FFT |
受信信号のガードインターバル部分を消去する。
FFTして復調を行う。 |
| //Parallel to serial data_7 = data_6; subplot(2,2,4); a = get("current_axes"); xtitle("The result after FFT"); a.data_bounds = [-3,-3;3,3]; plot(real(data_7),imag(data_7),'r.'); |
復調シンボルのコンスタレーションを表示する。 |
| // data decode for j=1:num_symbol for i=1:num_point if (real(data_7(i,j))>=0 & imag(data_7(i,j))>=0) then decdata(i,j)=0; elseif (real(data_7(i,j))<0 & imag(data_7(i,j))>=0) then decdata(i,j)=1; elseif (real(data_7(i,j))>=0 & imag(data_7(i,j))<0) then decdata(i,j)=2; else decdata(i,j)=3; end end end |
コンスタレーションの値より、0から3の元データに変換する。 |
| // calculate number of different data diff1 = data - decdata; diff2 = sign(abs(diff1)); serr = sum(diff2) // error symbols tsym = num_point*num_symbol // total number of symols mprintf(' SNR(dB)= %3d SYMBOL ERROR RATE = % 5.4e \n', sn, serr/tsym); |
元データと受信データの違う個数を数える。
全データ数との比がシンボルエラー率となる。 |

宿題8
(1)上記SCILABプログラムを利用して、1KFFT、QPSKを用いるOFDM伝送での、
シンボルエラー率 vs SN比の関係を示すSEMILOGのグラフを作成せよ。
SN比は0から10dBで1dBステップとする。
(2)上記SCILABプログラムを利用して、変調方式がBPSKでコンスタレーションが”1”もしくは”−1”の場合の
シンボルエラー率 vs SN比の関係を示すSEMILOGのグラフを作成せよ。
(3)上記2つのシミュレーションの結果から言えることを全て述べよ。
以上