（7）電波伝搬とZ変換

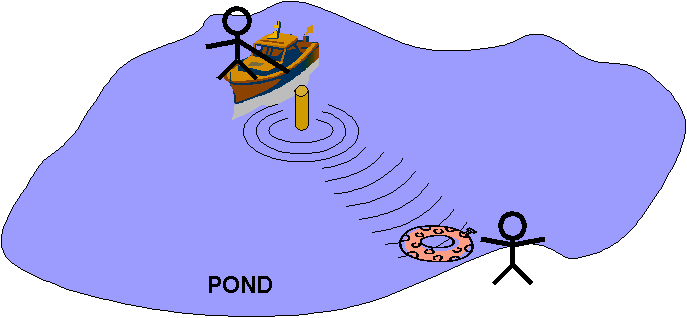
〇　電波伝搬とは　：　電波が空間を伝わること

１）送信アンテナから離れると　電波のパワーが減衰　図６−１�@

２）壁や物質を通過するときに減衰　図６−１�A

３）物陰の奥では減衰　（シャドウイング）　図６−３�B

周波数が高くなると電波が回り込みにくくなる（回折率が周波数に反比例）

〇マルチパス

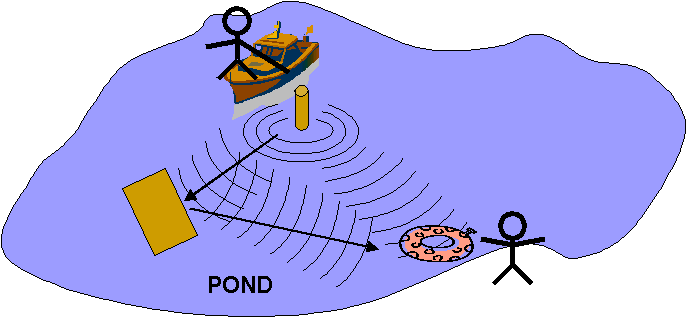
• 無線通信ではかならずマルチパス(Multipath)が発生する。

• やまびこ　「音声波が山などから反射して時間差で聞こえる現象」

• マルチパスとは複数の経路から伝わる反射波

• 特徴：

  1. 同じ波が時間差で送れて到着する

  2. 受信アンテナで足し合わされる　（波は基本的に周期的な正弦波なので、足し合わさったり、消しあったりする。）

教科書　図６−４　：　白い部分：強めあう、黒い部分：弱めあう、約電波の半波長

　　光速C=3x10⁸(m/s)、f=100MHz、波長λ=C/f=3m

教科書　図６−５

　　ワイヤレスLAN　f=2.45GHz、波長λ=C/f=12.2cm

室内のワイヤレスLANでは5-6cmごとに電波の強度が変化している。

　　地上デジタル放送：　ch1(UHF=13)=473MHz、波長λ=C/f=63cm

約30cmごとに電波の強度は変化している。

〇マルチパスの表現

例　

送信アンテナから受信アンテナの直接距離　10Km

反射波の経路が12Kmとすると、

時間差Δｔ1は　2Km = C * Δｔ1より、Δｔ1=66.7us (μ秒　10^-6秒)

直接波と３つの遅延波のある場合　：　図６．７、縦軸はその信号のパワー（その経路を通過するときの減衰量）

お風呂の話：　P199　｢実生活における現象｣

〇マルチパス合成波形    SAILABによるプログラム　　channel.files/multipath1.sce

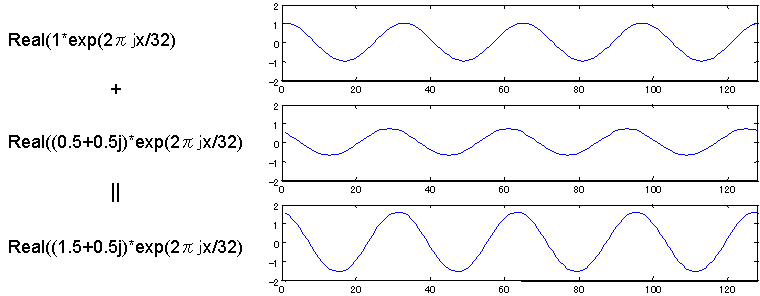
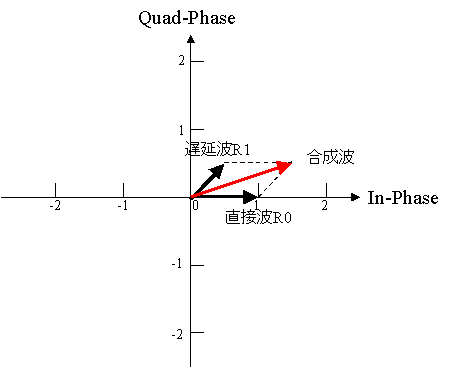
〇直接波と遅延波の合成はフェーザー（複素振幅表示を使用すれば非常に簡単にやることができる）

直接波R0の複素振幅　＝ 1.0

遅延波R1の複素振幅　＝ 0.5 + 0.5 j

合成波の複素振幅　＝　1.5 + 0.5j  

合成波の振幅は（赤線の長さ）＝sqrt(1.5² + 0.5²)=1.58

宿題６

（１）以下の複素振幅をもつ多数はの合成後の振幅はいくらか, 上記例のようにSAILABで波形で確認もせよ。

R0: 1+0j

R1: 0.5 -0.5j

（２）以下の複素振幅をもつ多数はの合成後の振幅はいくらか, 上記例のようにSAILABで波形で確認もせよ。

R0: 1+0j

R1: -0.5 -0.5j

R2: 0.3+0.7j

（３）450MHzの正弦波が無線伝送されている。

その電波を振幅の変化無しでどの程度の時間遅延させて合成すると、合成後の振幅は０となるか？また、振幅をが丁度sqrt(2)になる遅延量はいくらか？、また丁度振幅が２倍になる遅延量はいくらか？

上記解答をSCILABで確認せよ。

以上