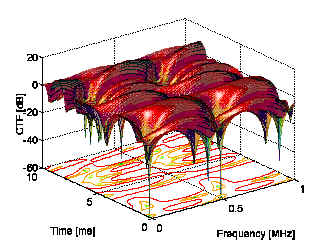
縦軸はパワーであり、移動しているので、時間方向に受信パワーが変動している。
〇マルチパスでは、波の重なりにより、空間の場所により波が強めあったり、消しあったりする。
縦軸はパワーであり、移動しているので、時間方向に受信パワーが変動している。
〇マルチパス・フェージングの解決方法 P202 表6−1
空間ダイバーシティ: 複数のアンテナを 1/2波長以上離して配置し、切り替えたり、合成したりする。
周波数ダイバーシティ: 通信する周波数チャネルを切り替える
偏波ダイバーシティ:
スペクトラム拡散(CDMA)を使う:
〇シンボル間干渉や歪の軽減
通信路等化
パイロットシンボル
OFDM
〇マルチパスの定式化 P203 6−4
一定遅延要素によるモデル : 電波が伝送される空間のモデル
図6−11 このような回路を FIRデジタルフィルターという。 Finite Impulse Response Filter
遅延演算子 Z-1
送信電波を インパルスで表す
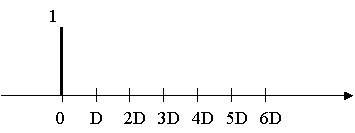

受信電波
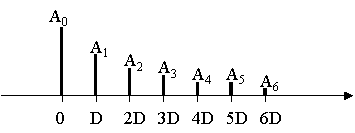
〇通信路のチャネル応答(伝達関数) P205
![]()
FIRフィルター
〇伝達関数の逆数
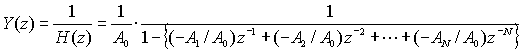
IIRフィルター
〇 IIRフィルターにより 遅延波を消すことができる。 ゴーストキャンセル!

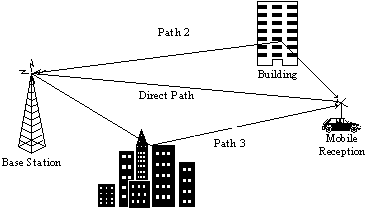
教科書の例にしたがって、上記通信経路で、Path2はDirect
PathよりTs遅れて
電波が到達し、その電波の振幅は0.5倍とし、
Path3はDirect Pathより2Ts遅れて
電波が到達し、その電波の振幅は0.2倍とすると
伝達関数をZ変換で表すと
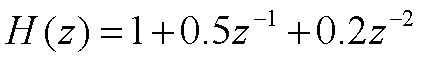
となる。
このチャネル(伝搬路)を [ 1 1 1 1 1] なる振幅1の信号が5個連続で通過すると仮定すると
その信号を以下のように表すことができる。
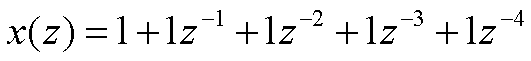
そうすると、車側での受信信号を以下のように計算することができる。
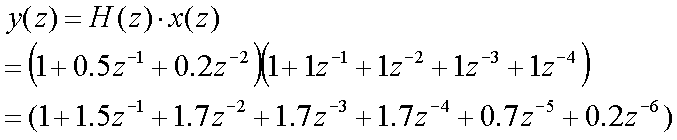
受信側では、マルチパスにより [1 1 1 1 1]
なる信号が[1 1.5 1.7 1.7 1.7 0.7 0.2]のようにエコーがかかった
信号となる。
以下に3種類入力信号にたいするSCILABシミュレーションの結果を示す。
コードはこちら channel2.files/multipath2.sce
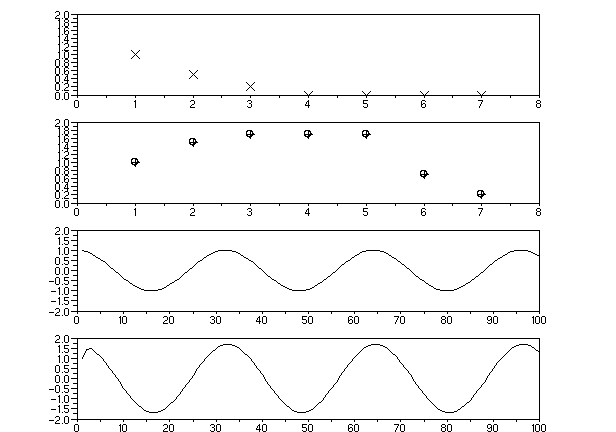
〇受信レベルの分布(変化)
レイリー分布 : 直接波がなく、同じレベルの複数の反射波がある。
仲上ライス分布 : 直接波があるか、特定の強いレベルの波はがある場合。
P210 図6−17: 受信レベル(振幅)が大きく変動する。
宿題7
(1)以下の伝達関数に(0,0,0,0,1,0,0,0.0)なる波形を入れるとどのような波形が出力されるか?
(0,0,0,0,1,1,1,1,0,0,0,0)なる波形を入力した場合どのような波形が出力されるか?
![]()
Z変換での多項式での計算結果と、SCILABでのシミュレーション結果の両方を示せ!
(2)上記伝達関数の逆数関数Y(z)を求め、図6−15、6−16と同様に遅延波をキャンセルできるかどうか検証せよ!
以上