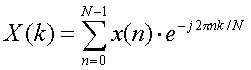
【離散フーリエ変換】
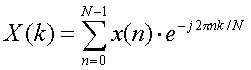
【Z変換】
離散時間信号x(nT)の複素数zに関する変換
すなわち、x(nT)なる離散時間信号を複素数zの関数に変換できる
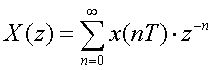
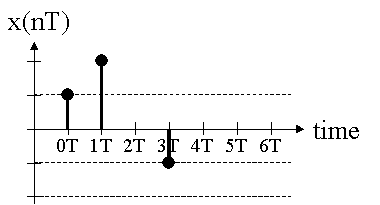
(例1)
(1) 時間nT=0, T, 3Tでの単位インパルス関数の和
![]()
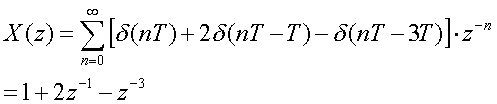
(2)単位ステップ関数
![]()
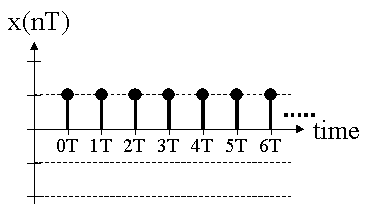
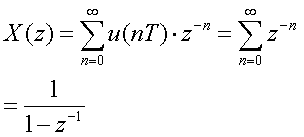
●主な離散時間信号のz変換
| (1)単位インパルス関数 | 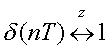 |
| (2)単位ステップ関数 | 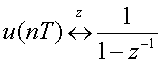 |
| (3)ランプ関数 | 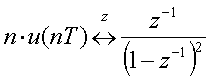 |
| (4)指数関数 | 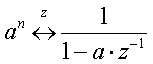 |
| (5)正弦波 | 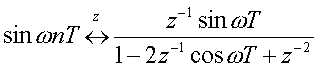 |
●Z変換のおもな性質
| (1)時間シフト | 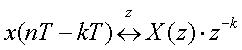 |
| (2)時間領域畳み込み | 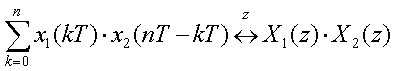 |
〇COLUMN4
通信路の応答は、時間軸では畳み込み、周波数軸では掛け算になります。
z変換で通信路をH(z)で示すと、周波数の意味をあいをもつ伝達関数を表しており、畳み込みではなく、掛け算で計算できます。
●上記のように、z変換の世界では、K時間の遅れはz-kを掛けることになり、単位時間の遅延はz-1を掛けることになります。
したがって、単位時間の遅延を素子を以下のように示すと分かりやすいです。
![]()
●因果性を満たす、線形時不変システムの応答
インパルス応答がh(nT)で示されるシステムにx(nT)の入力信号を入力するとき、出力y(nT)は畳み込みで表現される。
![]()
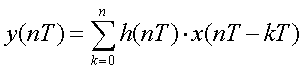
これをZ変換で表すと、上記性質より
![]()
となり、伝達関数H(z)
が以下のように定義できる。
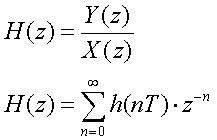
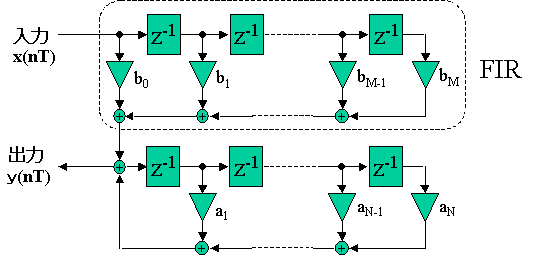
そして、教科書P205-207に示したように、伝達関数H(z)からすぐに、FIRやIIR型のフィルター回路を実現することができる。
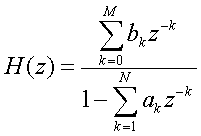
以上