Compiler Construction Lecture 12/09

先週の復習

先週は、

分割コンパイル
変数のscopeと型
Micro-C の記号表管理

について勉強したのであった。これを思い出しながら、今日は構文解析の実際について勉強しよう。

再び構文解析

今までは、再帰下降法(Recursive Decent)という構文解析方法を使ってきた。この方法は十分に高速だし、十分に一般的である。また、プログラマにとって、コンパイラの処理状況が直接的に見えるという利点もある。しかし再帰下降法では、文法規則そのものを、そのままプログラムの構造とすることが必ずできるわけではない。例えば、左再帰は、while などを使わなくてはいけなかった。

文法規則は、一般的に以下のような形で表される。

aexpr  :   aexpr '-'  mexpr 
       |   aexpr '+'  mexpr ;

このように、: の左が一つのシンボル(non-terminal symbolという)しかない文法は、Conext Free Grammar(CFG, 文脈自由文法)と呼ばれる。これは構文解析のアルゴリズムがあることが知られている。左のシンボルが複数あるようなものは、Contex Dependent Grammar(文脈依存文法) と呼ばれる。Context Dependent Grammarを一般的に構文解析することは決定不能(undecidable)であることもわかっている。もし、文脈自由文法で、再帰呼び出しがないのならば、それはFinite State(有限状態遷移) であり、その場でただちに構文解析される。高度な文法を使用したから、構文が読みやすくなるわけでもないが、有限状態遷移で表現されるような文法では、例えば、「()の対応」などを記述することはできない。これは若干不便だといわれても仕方がない。

したがって、ここで扱うコンパイラは基本的には、CFG(のsubset)を対象とすることになる。CFGのsubsetを自動的に構文解析するプログラムを生成することは可能であり、 Unixのyacc、GNU projectのbisonなどが知られている。yacc では、shift-reduce によるLR grammarの構文解析プログラムを生成することができる。再帰下降法を思い出そう。前出の文法は以下のようなプログラムで構文木の生成を実現できるのだった。

node *
aexpr()
{
    node *d;

    d = mexpr();
    while(last_token!=EOF) {
	switch(last_token) {
	case '-': 
	    d = new_node('-',0,d,mexpr());
	    break;
	case '+': 
	    d = new_node('+',0,d,mexpr());
	    break;
	default:
	    return d;
	}
    }
    return d;
}

ここでは、以下のことに注目して欲しい。

文法規則一つについて、一つの木が返される
この手続きからreturnする場合と、他の手続きを呼び出す場合がある

ごく当り前のことだ。この手続きからreturnする場合は、文法要素が確定した時であり還元(reduce)と呼ばれる。他の手続きを呼び出す場合は、遷移 shift と呼ばれる。reduce はスタックが減り、shift はスタックが増す。CFGのあるsubsetでは、このshift, reduce の組を状態遷移で表すことができる。すると、構文解析プログラムは、その状態遷移を行う機械となる。そして、reduce をおこなう部分に木を返す手続きを記述すれば良い。これが、yacc の原理である。例えば、この構文解析を yacc で記述すると以下のようになる。

aexpr :  aexpr '+' mexpr { $$ = new_node('+',0,$1,$3); }
    |    aexpr '-' mexpr { $$ = new_node('-',0,$1,$3); }
    |    mexpr {$$ = $1; }
    ;

$$ が返す木を表し、$1,$2,$3... などが文法規則中に現われた要素の木を表す。返す木の型(ここではnode *)は、YYSTYPEを#defineすることによって定義できる。実際には、木以外のものでも構わない。C の union などを使ってより自由度をあげることもできる。構文解析部分以外は、 s-tree-compile.c と、まったく同じものを使うことができる。例えば、 s-yacc.y のように記述することができる。yacc に -v option を付けてコンパイルすることにより、生成された状態遷移を見ることができる。

曖昧な文法

それでは、これで yacc を使えば、構文解析はすべてOkなのだろうか? 実際のコンパイラでは、さまざまな問題がある。例えば、

statement :  if ( expr ) statement
          |  if ( expr ) statement else statement
          |  a | b | c
          ;

という文法を考えて見よう。if (x==y) if (z==w) a else b は、どのように解釈されるべきだろうか?

if (x==y) { if (z==w) a else b  }
if (x==y) { if (z==w) a } else b

の2種類の解釈が可能である。(これは、間違いやすい部分でもある。僕だったら、 {}は省略しない。) これは、曖昧な文法と呼ばれる。CFGは、曖昧さを許す文法であり、実は人間は曖昧な文法の方が読みやすいし書きやすいと感じるようである。

実際には、このような文は、適当な規則により適当な解釈に固定される。逆にいえば、yacc がこのような曖昧な文法にであった時には、それを解決しなければならない。(状態遷移には曖昧さは許されない) このような曖昧さに出会った時に yacc は、shift reduce conflict とか、reduce reduce conflict という文句をいう。

yacc では、この場合は先に書いてある文法規則が優先される。つまり、二つ目の解釈になる。しかし、それが常に望ましいとは限らない。このためのいろいろなオプションがyaccには用意されている。

例えば、演算子の順位を指定することにより曖昧さを解決することもできる。例えば、四則演算だったら、

%left '+' '-'
%left '*' '/'
expr :  expr '+' expr { $$ = new_node('+',0,$1,$3); }
    |   expr '-' expr { $$ = new_node('-',0,$1,$3); }
    |   expr '*' expr { $$ = new_node('-',0,$1,$3); }
    |   expr '/' expr { $$ = new_node('-',0,$1,$3); }
    |   term   /* $$=$1 は省略可能 */
    ;

と記述することもできる。%leftが、左再帰を表し、その出現順序が演算子の優先順位を表している。

ここでは、yaccの実現や他の機能にはあまり深入りしないことにしよう。ただ、yacc の conflict はエラーではなく、曖昧な文法を表していて、yacc が勝手にそれを解決しているということは覚えておこう。conflict は文法の間違いを表していることも多いが、特に直す必要がない場合も多い。

モードに依存する文法

文法規則だけでは解釈する情報が足りない場合がある。例えば、

Cのtypedefのように、文法要素をプログラム中で定義する場合
演算子と、その順位をプログラム中で決める場合
global変数とlocal変数のように、同じ文法要素でも、出て来る位置により意味が違う場合

このような場合は、文法解釈の途中で、さらに文法構造とは別のモード(mode)を用意する。あるいは、いったん曖昧なまま構文木を作ってしまい、その後に解釈を行う方法もある。しかし、いったん木を作った後、木の構造を操作すると見通しが悪く間違いを起こしやすい。構文解析の途中で、mode を設定する方法が直観的で分かりやすいことも多い。例えば、 Cの文法は、かなり複雑であるが、modeを使うと簡単になる部分がある。

例えば、Micro-C では、Cの以下の宣言を一つの文法で済ましている。

global変数/関数の宣言
関数の引数の宣言
local変数の宣言
構造体の宣言

これらは、mode 変数の、

    45	#define TOP	0
    46	#define GDECL	1    /* global 変数 */
    47	#define GSDECL	2    /* global struct */
    48	#define GUDECL	3    /* global union */
    49	#define ADECL	4    /* argument 変数 */
    50	#define LDECL	5    /* local 変数 */
    51	#define LSDECL	6    /* local struct */
    52	#define LUDECL	7    /* local union */
    53	#define STADECL 8    /* static */
    54	#define STAT	9    /* function の最初 */
    55	#define GTDECL	10   /* global typedef */
    56	#define LTDECL	11   /* local typedef */

によって区別されている。getsym() では、このmodeを見ながら、どの処理を変えている。ただし、このmodeによる区別はプログラムの見通し悪くするので使い方には気を付けよう。

型のコンパイル

C では、変数の宣言は以下のように行われる。

     int i,*ptr;

これが、表れる場所によって、global変数やlocal変数となる。シンボル表の登録は、getsym()によってglobalとlocalに分けて、行われるので、getsym() が呼ばれる前に、 mode が決まっていなければならない。シンボルのsymbol classやdispの設定は、def() でやはりmodeを見て行われる。def() では、初期値の設定もおこなわれる。

ここで型名には、いろいろなものがくる。

前もって定義されている型 char,int,short,long,unsigned
* pointer 型
[]配列、()手続。これらは()でくくられる場合が多い
struct, unicon さらに中身の定義がある場合とない場合がある
typedef で定義された型名

しかも、この型名の構文は、通常の関数の定義と、cast (型変換の場合で異なる。例えば、関数へのポインタの宣言と、関数へのポインタの大きさを取る場合では以下のようになる。

int (*func)();
j  = sizeof(int (*)());

前者は typespec()とdecl0()で処理され、後者は、typename()とndecl0() で処理される。これを例えば以下のように使うことができる。(まるでアセンブラのようだ...)

func  = (int (*)())i;
return (*func)(j);

二つの処理がどのように異なるのかを調べて見よう。

制御構造のコンパイル

コンパイラ全体の中から見ると制御構造のコンパイルは、それほど大きくない。 statement()という一つの構文要素の中で閉じている。例えば、doif()では、 if文の処理をおこなう。

   742  doif()
   743  {int l1,l2,slfree;
   744          getsym();
   745          checksym(LPAR);
   746          slfree=lfree;
   747          bexpr(expr(),0,l1=fwdlabel());
   748          lfree=slfree;
   749          checksym(RPAR);
   750          statement();
   751          if(sym==ELSE)
   752          {       if (l2 = control) jmp(l2=fwdlabel());
   753                  fwddef(l1);
   754                  getsym();
   755                  statement();
   756                  if (l2) fwddef(l2);
   757          }
   758          else fwddef(l1);
   759  }

l1=fwdlabel()というのが未来に使うラベルの生成を行っている。ラベルの位置が決まった時点でfwddef(l1)を行う。 if文にはelse 節がある場合があり、その場合には、ラベルは二つ必要である。 (controlの役目はなにか?)

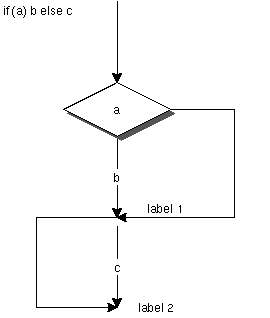
これと、ラベルにjumpするjump(label)を使えば、ほとんどの制御構造のコード生成が可能となる。残りは、switch文やreturn文、そして、関数呼び出しである。

条件分岐の取り扱い

条件分岐は、構文解析はexpr()を使うが、コード生成がgexpr()とは異なり、 bexpr()により処理がおこなわれる。bexpr()は、引き数として、構文木、条件、ラベルを取り、構文木の一番上が条件比較だったら、それお条件分岐に書き換えている。

  1560  bexpr(e1,cond,l1)
  1561  int e1,l1;
  1562  char cond;
  1563  {int e2,l2;
  1564          if (chk) return;
  1565          e2=cadr(e1);
  1566          switch(car(e1))
  1567          {case LNOT:
  1568                  bexpr(e2,!cond,l1);
  1569                  return;
  1570          case GT:
  1571                  rexpr(e1,l1,cond?"GT":"LE");
  1572                  return;
  1573          case UGT:
  1574                  rexpr(e1,l1,cond?"HI":"LS");
  1575                  return;

宿題

木曜日までに提出して下さい。E-Mailでもいいです。答案用紙を提出すれば出席とします。

(1)
```
    j  = sizeof(int (*)());
```
が、どのようにコンパイルされるかを、文字列と手続名と行番号の対応で示せ。 (ヒント、sizeof は、expr13()にあります。dbx とかを有効に使うと楽勝) 単なるtraceだと何が何だか分からないと思います。
(2)
doif() の処理中で、control という変数を見ているが、これは、どこで、何のために設定されているのかを示せ。

prev
next

lecture top