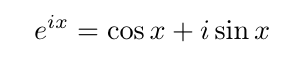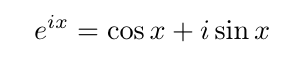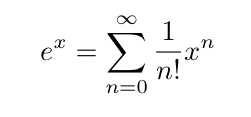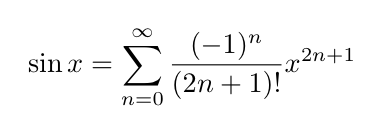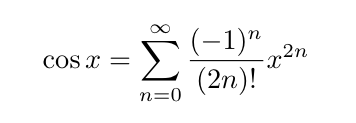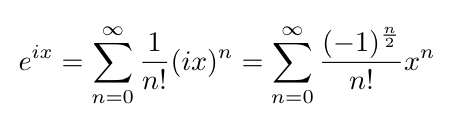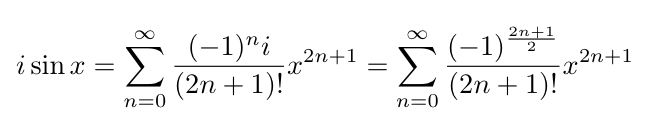2007/06/06更新
オイラーの公式
ここでは、オイラーの公式について説明します。
事前にテイラー展開(Talor Expansion)を理解しておく必要があります。
オイラーの公式とは
指数関数と三角関数は、複素数空間において可換であることを示す。
指数関数は一見すると三角関数と無関係に思える。しかし、これらの関数を複素関数と捉えることで、
以下のような置き換えが可能である。
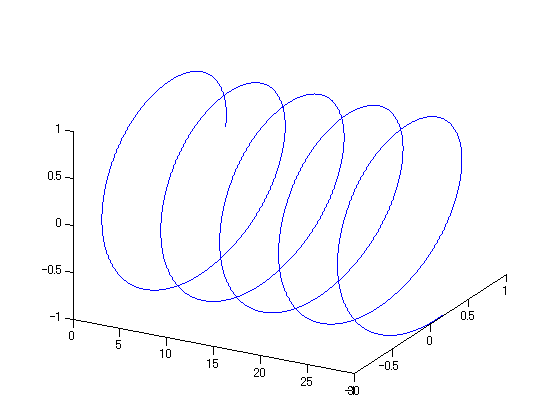
これを可視化すると、下のようにソレノイド(ばね)グラフになる。
指数関数と三角関数のベキ級数展開
指数関数e^xと、sin(x)、cos(x)のベキ級数展開は、それぞれ、
となる。
よって、e^ixは以下のようになる。
また、isin(x)は次のようになる。
ここで、各関数の係数の複素数レベルでの正負を比較する。
e^ixの係数の正負の変化は、
+1,+i,-1,-i,....
というパターンの繰り返しである。
cos(x)は、
+1,-1,+1,-1,....
の繰り返しである。
isin(x)は、
+i,-i,+i,-i,....
の繰り返しである。
よって、cos(x)+isin(x)の正負の出現パターンは、
+1,+i,-1,-i,....
となり、e^ixと完全に等くなる。
その後、e^ixとisin(x)のシグマを展開すれば、オイラーの公式が正しいということがわかる。