2005/9/30 ver 1.1修正 1箇所赤字で修正
琉球大学工学部情報工学科 和田 知久
最近では携帯電話、地上デジタル放送など移動体での無線通信の発達が著しく、またLSIの進歩に伴って非常に複雑な信号処理を適用して、無線通信システムの高性能化が実現されてきています。昨年度はデジタル方式のFMレシーバー回路を設計し、デジタルデータの伝送を行いました。しかしながら、実際のデジタル通信ではエラー訂正技術を用いて、伝送されたデジタルデータに対してエラー訂正処理を行い、データ転送の信頼性を向上させています。最近、シャノンの理論限界に迫る高性能を実現するエラー訂正方式としてターボ符号や低密度パリティ検査符号が注目され、一部で実用化が開始されています。ターボ符号では送信側(エンコーダ)の構成は単純ですが、受信側(デコーダ)では同じデータに対して繰り返し処理を行いエラー訂正能力を向上させています。
このコンテストは学生対象のコンテストですので、ターボ符号等は課題が大きすぎることもあり、今回はターボ符号デコーダと似通った繰り返し処理を用いる2次元積符号のデコーダ回路を設計します。送信情報はエンコーダにて2X2の2次元配列に並べられます。その2行2列のそれぞれに対してパリティビットを生成します。2行2列ですので、全部で4ビットのパリティが生成されます。したがって、送信情報4ビットにパリティ4ビットが付加されて、8ビットがひとつの処理単位となります。この8ビット情報がBPSK方式で変調され、送信されノイズの影響を受けます。受信側ではこのノイズの影響を受けた信号の復号、すなわちエラー訂正を行います。
学生対象のコンテストですので小さめのデジタル回路を設計することを念頭に、なるべく簡単な回路構成要素を組み合わせて繰り返し型のデコード行う回路を設計します。要求されている設計内容はHDL(VHDLもしくはVerilogHDL)による設計と論理合成です。特にシノプシス社の合成ツールを使用する必要はなく、FPGA等の合成ツールでも参加できます。HDL設計に興味のある学生はどしどし参加してください。また、余裕のある方はFPGA等で実装すれば、努力を認めて高い評価が得られると思います。FPGA等での実装もぜひトライしてみてください。

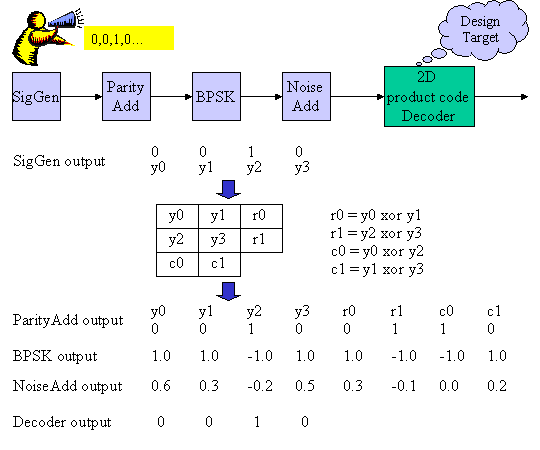
図1 システム図
図1に今回想定するシステムのブロック図を示します。システムは大きく分けて、送信情報生成部(SigGen)、そのSigGenの出力の情報ビットにパリティ検査ビットを付加するパリティ付加部(ParityAdd)、0もしくは1のデジタル値を、それぞれ 1.0, -1.0に変換するバイナリ−シフトキーイング変調部(BPSK)、そして実際のワイヤレス伝送時のノイズの印加に対応するノイズ印加部(NoiseAdd)、そしてそのノイズの印加されたBPSK信号を受信し、エラー訂正を行う2Dproduct code Decoderから構成されます。
図1をみてもわかりますが、送信情報4ビットに対して、さらに4ビットのパリティビットを付加して、8ビットに変換します。この8ビットはBPSKで8個の1.0もしくは-1.0なる実数値に変換され、通信路でのノイズの影響で、この8個の実数値は異なる値になります。受信Decoderでは8個の実数値を受け取り、これをもとにエラー訂正を行い送信情報ビット4ビットの復号を行います。
図2に2次元積符号の構成方法を示します。SigGen出力は4ビットごとにグループ分けされています。この4ビットを{y0, y1, y2, y3}とし、図のような2X2の正方行列を作成します。各行、各列に対して1ビットのパリティ検査ビットを付加します。行のパリティをそれぞれ、r0、r1、列のパリティをc0、c1とします。
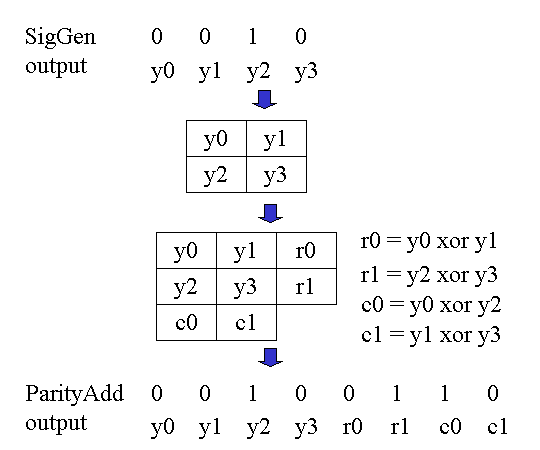
図2 2次元積符号
この4つのパリティビットをもとの4ビットの情報ビットに連結し、{y0, y1, y2, y3, r0, r1, c0, c1}なる8ビットの2次元積符号を生成します。余談ですが、4ビット情報に対して送信ビットは8ビットですので、このような符号をコードレイトR=1/2 (= 4bit/8bit) なる符号と言います。
実際に0、1なるデジタル情報を無線で送信する場合には、電波の波を使って情報を伝送することになります。BPSK変調は位相が0°と180°の異なる2種類の波を使って伝送することです。ここでは、BPSKの説明は省略しますが、cos(0 degree) = 1.0, cos(180 degree)=-1.0ですので、ここではデジタル情報”0”に対して実数1.0を、デジタル情報”1”に対して実数−1.0を伝送します。この様子を以下図3の上半分に示します。1.0と-1.0の中間値は0.0であるので、受信側では受信信号が0.0より上であれば、送信データは”0”、0.0より下であれば”1”と復調することができます。
このBPSK変調された信号は電波として伝送され、受信機側にとどく間にノイズが加えられます。ここでは最も一般的に用いられているランダムノイズ(加法性白色ガウスノイズ)を印加します。ランダムノイズには特徴があり、ノイズを長時間にわたって平均すると0となります。また、ノイズの振幅はガウス分布に従い、小振幅のノイズの出現頻度が高く、大振幅のノイズの出現頻度は低くなります。
一般的にBPSKのような送信信号と、ノイズの割合を定義するために、信号/ノイズパワー比(S/N比)が用いられますので、ここでもS/N比を用います。S/N比を定義するためには、信号パワーとノイズパワーを求め、その比を取る必要があります。信号パワーは信号振幅の2乗の平均で求められますので、今回のBPSKでは常に信号振幅は1.0もしくは-1.0ですので、その2乗は1.0であり、平均も1.0となり、信号パワーは1.0ということになります。
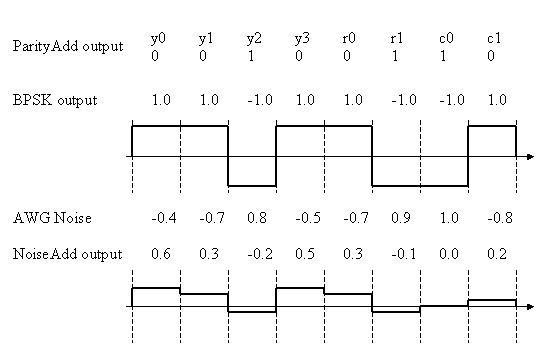
図3 BPSK変調とノイズ印加
また、図3のAWG Noiseがノイズ振幅であり振幅は{-0.4, -0.7, 0.8, -0.5, -0.7, 0.9, 1.0, -0.8}であるので、パワー平均は
Noise Power= 1/8*(0.16 + 0.49 + 0.64 + 0.25 + 0.49 + 0.81 + 1.0 + 0.64)=0.56 となり、
S/N比=1.0 / 0.56 = 1.78 となります。
一般にはこれを以下のようにでdb(デシベル)値に変換します。
S/N(dB) = 10*log10(1.78) = 2.5 dB (2005/9/30修正 1/1)
したがって、ここではS/N=2.5dBのノイズを印加したことになります。図3の最下段の波形はノイズ印加後の送信波形であり、この波形を受信側が復調します。受信信号{0.6, 0.3, -0.2, 0.5, 0.3, -0.1, 0.0, 0.2}と中間値0.0と比較することで、対応するデジタル情報を復元できますが、受信信号=0.0はちょうど中間値と同じですので、復元は困難です。しかしながら、この8つの受信信号はもとは4ビットの情報で、冗長性がありますので、エラー訂正処理を行えば正しく復調することが可能であり、今回の設計テーマとなります。
(3−1)事前確率と事後確率
今回は8個の受信した信号値 R={Ry0, Ry1, Ry2, Ry3, Rr0, Rr1, Rc0, Rc1}から、元の4ビットのデジタル情報値{y0, y1, y2, y3}を推定します。たとえば、y0は"0"か"1"の2つの場合しかなく、8個の信号値 Rを受信したとき、以下の2つの確率のどちらが大きいかを判断すればよいことになります。
1) あるRを受信したときの、送信情報 y0 が"0"である条件確率
![]()
2) あるRを受信したときの、送信情報 y0 が"1"である条件確率
![]()
Rを受信する以前は、P(y0=0) = P(y0=1) = 0.5で同じ確率であるが、
Rを受信したことにより、P(y0=0 | R)とP(y0=1 | R)の大小に差が生じたことになります。専門用語では、Rを受信する前のP(y0=0) や P(y0=1)を事前確率といい、Rを受信した後の P(y0=0 | R)やP(y0=1 | R)を事後確率といいます。
(3−2)対数事後確率比(事後値)
上記2つの事後確率の大小比較を行う別の方法として、対数事後確率比(事後値)Λ(y0)を定義します。
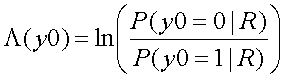
これは上記2つの事後確率の比の自然対数を取ったものです。これにより、確率の大小関係の判断の代わりに、事後値が正か負かで判断できることになります。すなわち、Λ(y0)>0であれば、P(y0=0 | R)>P(y0=1 | R)であり、Rを受信した時に、y0 = 0と判断することができます。
ベイズの公式より、
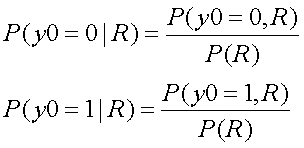
と変形できるので、
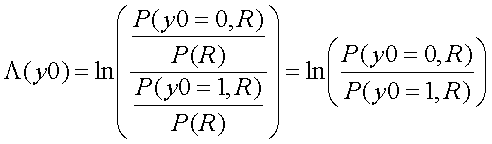
と変形することができます。
(3−3)事後値=通信路値+事前値+外部値の導出
ここで、P(y0=0, R)の意味を考えると、送信情報がy0=0でありかつ、あるR={Ry0, Ry1, Ry2, Ry3, Rr0, Rr1, Rc0, Rc1}を受信した確率です。ここで行方向のパリティの関係に注目すると、r0=y0 xor y1であるので、y0=r0 xor y1の関係が成立し、送信情報y0="0" ならば r0 xor y1="0"も成立していることになります。すなわち、以下のように変形可能です。(ここで、xorは排他的論理和です。)
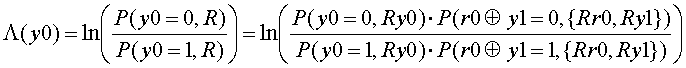
自然対数内の積は自然対数項の加算に変形できるので、
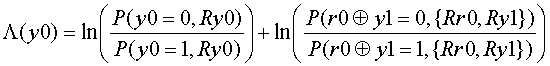
さらにこの1項目はベイズの公式により
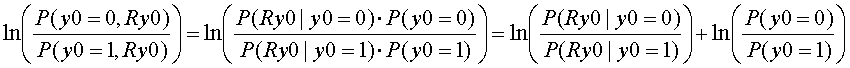
と変形できるので、
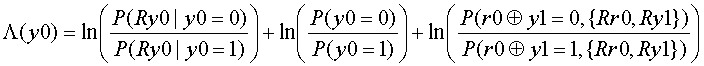
となります。これの意味を考えると、
1)第1項目はy0=0を送って、あるRy0受信する確率と、y0=1を送って、ある同じRy0受信する確率の対数比であり、これは送信チャネルのノイズの量すなわちS/N比によって決定される値です。したがって、この1項目を通信路値 Lch と呼びます。
2)第2項目は送信情報のy0が0である確率と1である確率の対数比であり、偏りのないデータを送信していると仮定すれば、第2項目は0です。これは、送信情報に関する項であり、事前値と呼びます。
3)第3項目はy0ではない、行のパリティで関連する他の部分の対数確率比に関する項であり、外部値 Le と呼びます。
すなわち、
事後値Λ = 通信路値Lch + 事前値 + 外部値Le
で事後値が計算可能となります。
(3−4)BPSK変調で白色ガウズノイズ印加時の通信路値の計算
BPSK変調すなわち、論理値"0"に対して信号1.0を、論理値"1"に対して信号-1.0を送出し、そこに白色ガウス雑音が加わると、図4上図に示すように1.0もしくは-1.0を中心に受信信号値が分散します。ガウス雑音ですので、受信信号の分布は正規分布に従い、式で表すと以下のようになります。
1)送信信号=1.0の場合
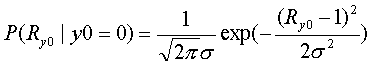
2)送信信号=-1.0の場合
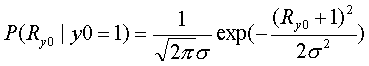
ここでσ2は雑音の分散です。
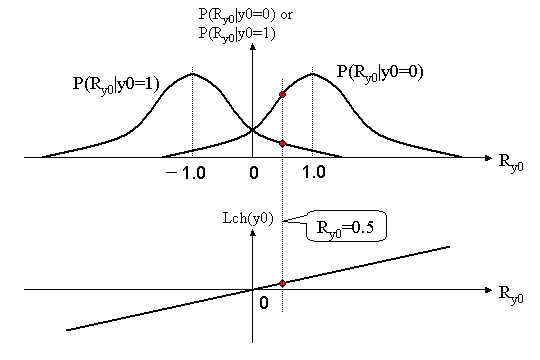
図4 白色ガウズノイズによる受信値の分散と通信路値
これより、通信路値Lchを求めると
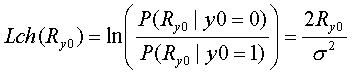
となり、Lchは受信信号Ry0に正に比例することになります。
(3−5)外部値の計算
3−3節で求めたように外部値は以下で表されます。
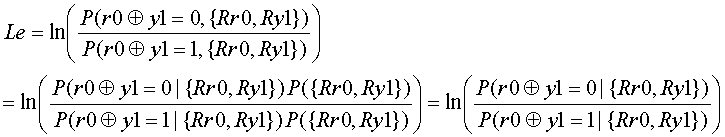
r0 xor y1=0 となるのは、r0=y1=0 もしくは r0=y1=1 となる場合であり、r0 xor y1=1となるのは r0=0, y1=1もしくはr0=1, y1=0 となる場合であるので、以下のように変形することができます。
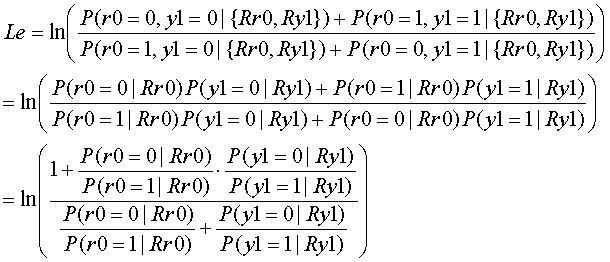
ここで、Λr0, Λy1を以下のように定義します。
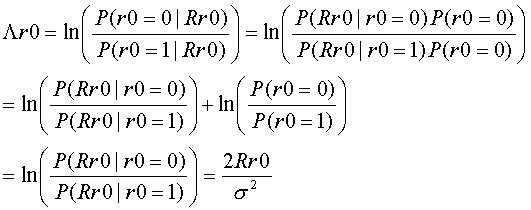
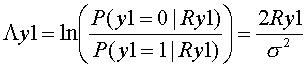
そうすると、以下のようになり、|Λr0|, |Λy1|の差が大きい場合には、
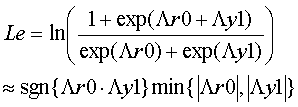
と近似することができます。sgn(Λr0* Λy1)はΛr0* Λy1の積の符号であり、正であれば1.0、負であれば-1.0を返す関数です。
min(|Λr0|, |Λy1|)はΛr0, Λy1の絶対値の小さい方を返す関数であす。
回路を構成するときは、Λr0, Λy1を変数として用いて、上記近似式を計算することになります。
3節で復号処理に関するアルゴリズムの基本式を導出しましたが、ここでは結果的にどのように復号するのかを説明します。
1)手順1: R={Ry0, Ry1, Ry2, Ry3, Rr0, Rr1, Rc0, Rc1}なる8つの実数値を受信
この8個の値から通信路値、外部値などを計算しますが、通信路値のLchは受信値に対して2/σ2を乗算し、外部値のΛの計算も同じく2/σ2を乗算する必要がありますが、結果的にすべての計算値に2/σ2が乗算され、最終的に事後値の正か負かの判断には影響しないので、ここでは2/σ2=1と簡単化して話を進めます。
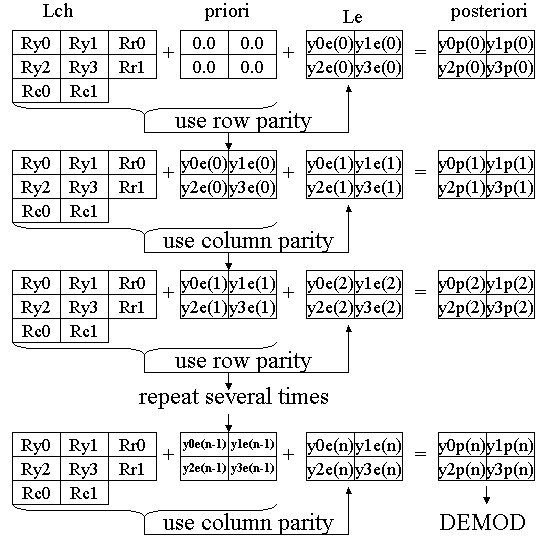
図5 繰り返し型の復号処理
2)手順2: 通信路値から行のパリティの性質を使って外部値を計算
図5の最上段に示すように、通信路値Lchと事前値prioriの加算を行う。ただし、初期であるので事前値はすべて0.0である。この和に対して、外部値Leを計算する。外部値LeはROWパリティの関係と、COLUMNパリティの関係から計算できますが、まずROWパリティの関係を用いて以下のように計算します。
y0e(0) = sgn(Ry1*Rr0) * min(|Ry1|, |Rr0|)
y1e(0) = sgn(Ry0*Rr0) * min(|Ry0|, |Rr0|)
y2e(0) = sgn(Ry3*Rr1) * min(|Ry3|, |Rr1|)
y3e(0) = sgn(Ry2*Rr1) * min(|Ry2|, |Rr1|)
sgn(Ry2* Rr1)はRy2* Rr1の積の符号であり、正であれば1.0、負であれば-1.0を返す関数である。
min(|Ry1|, |Rr0|)はRy1, Rr0の絶対値の小さい方を返す関数である。
実際にはこの外部値Leを次の繰り返しでの、事前値に使用するだけなので、事後値posterioriの計算は不要ですが、図のように事後値を毎回計算してもよい。
3)手順3: 上記外部値を次の繰り返しの事前値として使用し、列パリティの性質を使って外部値を計算する
図5の上から2段目に示すように、以下のように次の外部値Leを計算する。
y0e(1) = sgn( (Ry2+y2e(0)) * Rc0 ) * min(|Ry2+y2e(0)|, |Rc0|)
y1e(1) = sgn( (Ry3+y3e(0)) * Rc1) * min(|Ry3+y3e(0)|, |Rc1|)
y2e(1) = sgn( (Ry0+y0e(0)) * Rc0 ) * min(|Ry0+y0e(0)|, |Rc0|)
y3e(1) = sgn( (Ry1+y1e(0)) * Rc1) * min(|Ry1+y1e(0)|, |Rc1|)
4)手順4: 上記のように行パリティ、列パリティを用いた外部値計算を数回繰り返す
行パリティを用いた外部値の計算の一般式は
y0e(n-1) = sgn( (Ry1+y1e(n-2)) * Rr0 ) * min(|Ry1+y1e(n-2)|, |Rr0|)
y1e(n-1) = sgn( (Ry0+y0e(n-2)) * Rr0) * min(|(Ry0+y0e(n-2)|, |Rr0|)
y2e(n-1) = sgn( (Ry3+y3e(n-2)) * Rr1 ) * min(|Ry3+y3e(n-2)|, |Rr1|)
y3e(n-1) = sgn( (Ry2+y2e(n-2)) * Rr1) * min(|Ry2+y2e(n-2)|, |Rr1|)
列パリティを用いた外部値計算の一般式は
y0e(n) = sgn( (Ry2+y2e(n-1)) * Rc0 ) * min(|Ry2+y2e(n-1)|, |Rc0|)
y1e(n) = sgn( (Ry3+y3e(n-1)) * Rc1) * min(|Ry3+y3e(n-1)|, |Rc1|)
y2e(n) = sgn( (Ry0+y0e(n-1)) * Rc0 ) * min(|Ry0+y0e(n-1)|, |Rc0|)
y3e(n) = sgn( (Ry1+y1e(n-1)) * Rc1) * min(|Ry1+y1e(n-1)|, |Rc1|)
筆者の経験では、5,6回繰り返えせば十分のように思います。
5)手順5: 最後に事後値を計算し、復号を行う
事後値posterioriが正であれば、”0”であり、負であれば”1”に復号することができます。
これまで、復号アルゴリズムや繰り返しの復号処理を説明してきました。結構複雑に思われたかと思います。しかしながら、実際に回路にしてみると結構単純な回路構成で実現することができます。
以下にに繰り返し復号回路のある構成方法を説明します。図6は回路構成例で、図7はその動作タイミング図です。図では簡単のため、クロックCLK配線は省略されていますが、各フリップフロップに接続されます。
図7に示しめすように、4ビットの送信データsenddataに対して4ビットのパリティが後につなげられ、BPSK変調後送信され、ノイズの加えられた信号が8ビットのrxinに入力されます。送信単位(シンボル)の先頭を示すために、start信号も入力されます。8サイクルで、Ry0, Ry1, Ry2, Ry3, Rr0, Rr1, Rc0, Rc1}なる8つの実数値が受信されます。ここでは2の補数表現の8ビットを用いています。
Serial to Parallel変換回路で、8つの8ビット値がパラレル信号{y0[8], y1[8], y2[8], y3[8], r0[8], r1[8], c0[8], c1[8]}に変換されます。
start信号をリセット信号として用いて、外部値{y0e[8], y1e[8], y2e[8], y3e[8]}の初期値がリセットされます。各サイクルごとに行パリティを使った外部値を計算し、その外部値を事前値として列パリティを使った外部値が計算され、外部値が更新されます。
同時に事後値{y0p[8], y1p[8], y2p[8], y3p[8]}も更新され、8サイクル目の事後値のMSB(符号ビット)をstart信号で取り出すことにより、復号信号{y0d[1], y1d[1], y2d[1], y3d[1]}を出力します。
図中EXTVALブロックはこれまでも説明したように、入力A、Bに対して、
out = sgn(A*B) * min(|A|, |B|)
を計算する結構単純な組み合わせ回路ブロックです。
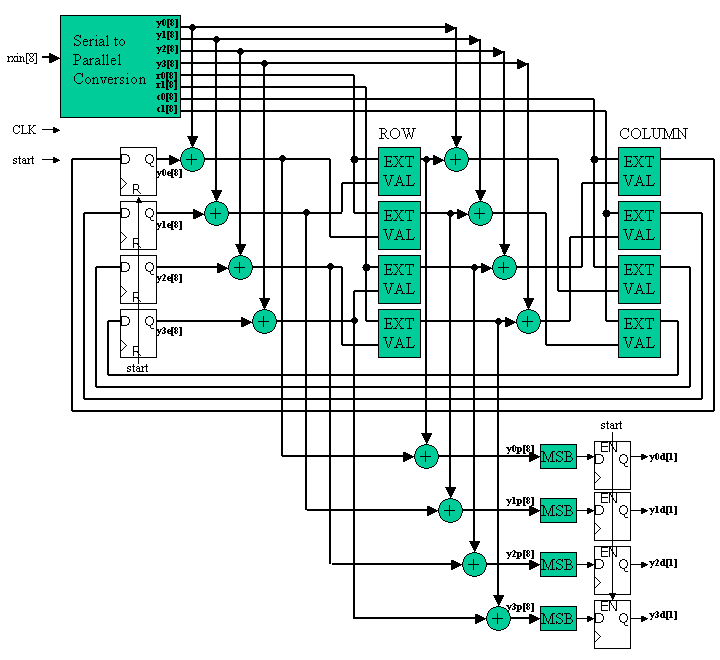
図6 回路構成例
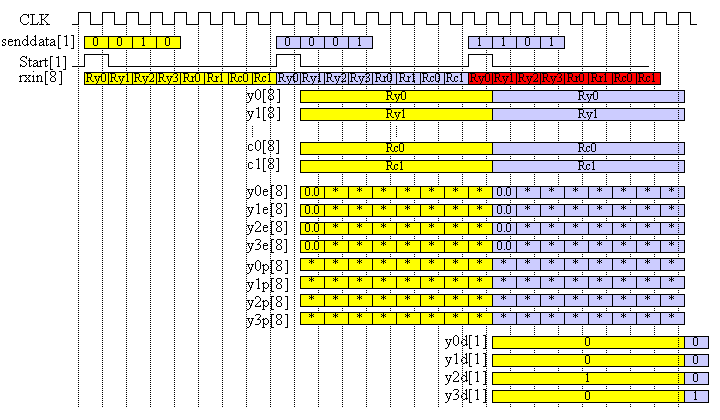
図7 回路構成例の復号動作タイミング
基本課題では図7に示すように、シリアルにやってくるrxinとstart信号をもとに復号出力{y0d[1], y1d[1], y2d[1], y3d[1]}を出力します。動作タイミングは図7は一つの例であり、同じにする必要はありません。自由に変更してください。
基本課題では、シリアルにやってくるrxinとstart信号から復号回路を設計し、S/N=0, 3, 6, 9dB条件での、10000ビットの送信データ中のエラー訂正に失敗したデータ数をレポートしてください。
表1 基本課題用ピンリスト
|
FMRX |
|||
| 信号名 | 入出力 | ビット幅 | 説明 |
| CLK | IN | 1 | クロック入力 |
| start | IN | 1 | ’1’でシンボルの先頭を示す |
| rxin | IN | 8 | 2の補数表現の送信信号 |
| y0d | OUT | 1 | 復調出力 |
| y1d | OUT | 1 | |
| y2d | OUT | 1 | |
| y3d | OUT | 1 | |
以下に、20000サイクル分のstart信号および、8ビットのrxin信号をリンクします。コードレイトが1/2なので、実際には10000ビットに対応する送信信号です。rxinに対しては S/N=0dB, 3dB, 6dB, 9dB, 100dBを用意しており、S/N=100dBはほとんどノイズのない送信波形です。
rxinは2の補数表現の8ビットデータですので、−128から127の数値を表現できます。ここでは、BPSKのノイズなしでの送信値を+32、−32としています。
それぞれに対して、復号動作を行い、10000ビットの送信信号に対して復号できなかったエラービット数を報告してください。正確な10000ビットの送信データsenddataも以下にリンクします。
start信号: start.txt
rxin信号(SN=0dB、ノイズ非常に大): rxin0DB.txt
rxin信号(SN=3dB、ノイズ大): rxin3DB.txt
rxin信号(SN=6dB、ノイズやや大): rxin6DB.txt
rxin信号(SN=9dB、ノイズ小): rxin9DB.txt
rxin信号(SN=100dB、ノイズなし): rxin100DB.txt
送信データ(10000ビット分): senddata.txt
初期の40サイクル程度の波形図を以下に示します。
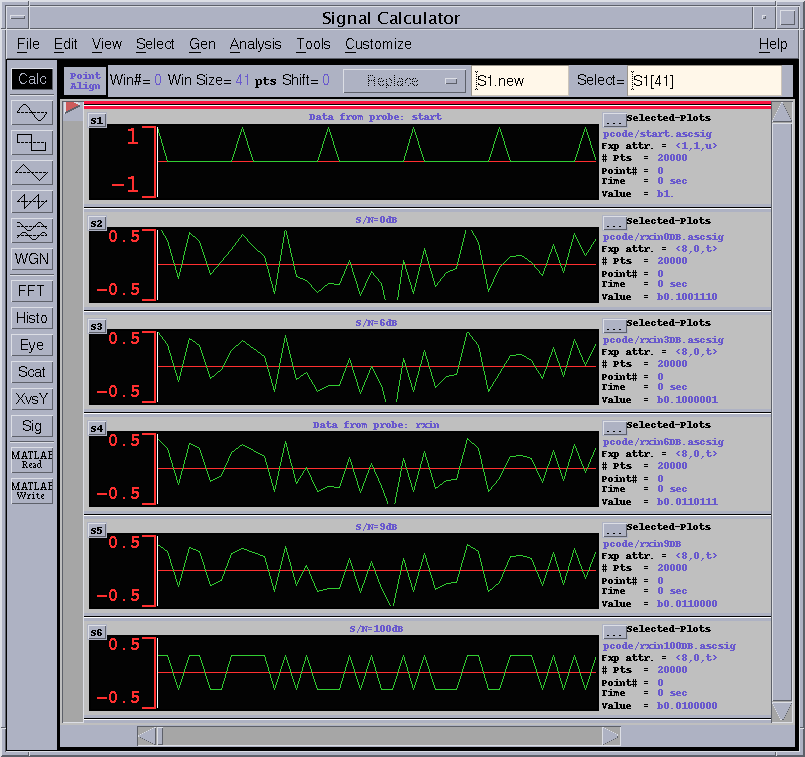
図8 入力波形図
最上段はstart信号であり、それ以下はSN=0dB, 3dB, 6dB, 9dB, 100dB条件でのrxin波形を示しています。
最下段はノイズのない信号であるので、BPSK信号を示しています。また、この表示では、8ビットの数を右へ7ビットシフトした値で表示しているので、BPSKの振幅は0.25、 -0.25と表示されています。
上級編では送信データとして、上記にリンクされている20000サイクル(送信データ10000ビット)の復号ができれば、どのような構成でもOKです。ユニークな方式を色々と考えてみてください。
案としては、
データは8ビットで与えられているが、回路としては8ビットすべてを使用する必要はなく、任意の精度で設計することにより高速化、省面積化を実現できるかも知れない。
データの入力がシリアルでなく、自由な構成にすることで、面白いアーキテクチャーを実現できるかもしれない。
EXTVALの計算を上記説明では、近似を行っているが、回路をつぎ込んで計算することで、エラー訂正能力を向上できるかもしれない。
また、今回繰り返し型のDECODE方式を説明しましたが、まったくこの方法を無視して、rxinの受信値から独自の方法で、DECODEする。
などです。
今回は回路面積、スピード(クロックサイクルタイム)以外に、エラー率も評価の対象になります。
琉球大学以外からの参加の場合、同一のシノプシスデザインコンパイラの論理合成用ライブラリを使用することが困難であるので、
とします。
具体的には、以下のような多段EXOR回路を例に従って合成し最適化し、その1段あたりの遅延時間を単位時間としてスピードの単位とします。
多段EXOR回路のVHDLソース例:50入力のEXOR回路
この例では6段のEXOR段が合成され、クリティカルパス遅延はreport_timingコマンドにより7.17であったので、7.17/6=1.195を単位(1UNIT_DELAY)とします。
例えば、ある遅延が20ならば、20/1.195=17.74UNIT_DELAYとします。
琉大情報のライブラリ使用者は上記値で換算すればよいです。
また、面積はreport_areaコマンドのtotal cell areaは147.0であり、EXORゲイト数は49個であるので、147.0/49=3.0を単位(1UNIT_AREA)とします。
レポートには以下の内容を含めるてください。また、ページ数を少なめにコンパクトにまとめてください。
| 表紙 | 1 | 代表者の氏名、チーム名、大学院修士/大学学部生/高専生の区別 |
| 2 | 共同設計者全員の名前(最高3名まで)、学籍番号、学年、学校名、住所、電話、email等連絡先 | |
| 3 | 全員のTシャツの希望サイズ(S,M,L,XLのいずれか) | |
| 4 | 取り組んだ課題(LEVEL1/LEVEL2) | |
| 内容 | 1 | 設計した回路ブロックの構成説明(ブロック図と説明) |
| 2 | 設計した回路ブロックの動作説明(動作波形図やパイプライン動作等の説明) | |
| 3 | 工夫した点、オリジナリティを出した点(アピールが重要!) | |
| 4 | クリティカルパスのスピード、論理合成後の回路規模、実現したS/N比とエラー数の関係 | |
| 5 | VHDLもしくはVerilogのコード | |
| 6 | 正常動作しているVHDL/Verilogシミュレーション波形 | |
| 7 | その他自由意見など |
レポートはPDFファイルにて下記にEMAILにて提出すること!
他の形式での提出希望あれば、相談してください。
締め切りは2006年1月27日(金)必着です。
萩原春生、トリケップス、”ターボ符号の基礎” 第3章
本LSI設計コンテストの学生部門の企画・実行、および沖縄での発表会は
主催:LSIコンテスト実行委員会
共催:琉球大学工学部情報工学科、株式会社沖縄産業振興センター、九州半導体イノベーション協議会
協賛: ソニーLSIデザイン株式会社
です。
ENJOY HDL! 沖縄で会いましょう!