琉球大学工学部情報工学科 和田 知久
今回はワイヤレスLANなどで使用される次期米国標準の128ビット共通鍵ブロック暗号AES(Advanced Encription Standard)のSubBytes変換回路の設計を行います。
AESの暗号化アルゴリズムは、128ビット(16バイト)の入力データに対し、4つの基本演算 ShiftRows / SubBytes / MixColumns / AddRoundKey を複数回繰り返し適用するものです。簡単に言えば、16枚のトランプがあったとして、それに対してシャッフルと、数字の変更を繰り返し行うことで、初期の16枚のトランプの数字の並びを暗号化してしまうものです。AESに関しては、下記fips-197に詳細が説明されています。
http://csrc.nist.gov/publications/fips/fips197/fips-197.pdf
学生対象のコンテストですので小さめのデジタル回路を設計することを念頭に、今回設計するのはAESの暗号化処理のすべてではなく、特に回路設計で楽しむことができるSubByte変換回路だけを設計します。機能は非常に単純であり、8ビットの情報を他の8ビットの並びに1対1の変換を行うだけです。したがって、256ワード×8ビットのROM(Read Only Memory)で変換テーブル(S-boxと呼ばれている)を構成するたけで、実現することも可能です。しかしながら、そのSubBytes変換は2の8乗のガロア体の逆元計算と簡単な行列変換であるので、そのような演算をアルゴリズミック実現することで小さく、高速で消費電力の小さい回路も実現できます。
要求されている設計内容はHDL(VHDLもしくはVerilogHDL)による設計と論理合成です。特にシノプシス社の合成ツールを使用する必要はなく、FPGA等の合成ツールでも参加できます。HDL設計に興味のある学生はどしどし参加してください。また、余裕のある方はFPGA等で実装すれば、努力を認めて高い評価が得られると思います。FPGA等での実装もぜひトライしてみてください。

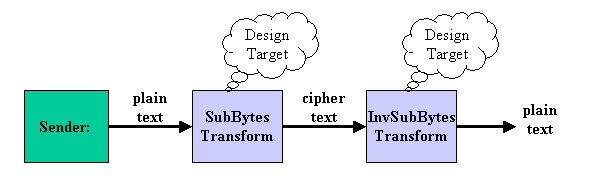
図1 システム図
図1に今回想定するシステムのブロック図を示します。システムは大きく分けて、8ビットすなわち、バイトデータ出力する送信部(Sender)、そのデータをリアルタイムで暗号化するSubBytes変換回路、その暗号化されたバイトデータを解読する逆SubBytes変換回路により構成されます。今回はモード切替によりSubBytes変換もしくは逆SubBytes変換の両方を実行できる変換回路を設計します。
今回の課題ではガロアの知識がなくても設計できるように、以下の仕様書でわかりやすく説明しています。設計すべきことは比較的単純ですので、デジタル設計の知識のある学生は自信を持って、課題に取り組んでください。
SubBytes変換は単に8ビットのバイナリ情報を他の8ビットのならびに変換するものです。
たとえば、00000000 なる全て0の8ビットの情報は 01100011 なる8ビットのビット列に変換されます。ここで重要なことは必ず異なる8ビットの数は異なる8ビットの数に変換されます。もし、2つの異なる8ビットの数が同一の8ビットの数に変換された場合には、変換後(暗号化後)の値からオリジナルの値に戻すことができなくなり暗号化システムには使用できません。
上記のような条件は
(1) 8ビットの数を変換しても8ビットの世界の中にいること(閉じている)、
(2) 一義的な逆変換ができること(逆元が存在する)
という特性があり、有限な数の世界の演算であるガロア体の性質を満たしています。後ほど、簡単にガロア体の説明もしてみます。
ということで、SubBytes変換は以下の2つの変換を直列に並べた変換により実現されます。
- 2の8乗のガロア体GF(28)の逆数に変換する (8ビットの数が異なる8ビットに変換される)
但し、00000000 (16進数表現{00})は 00000000 = {00}に変換されます。下記に逆数変換テーブルを示します。たとえば 01010011 なる8ビットの数は、16進表示で{53}となりますので、X=5, Y=3から表を引くと、{CA} なる16進表示が得られます。これを2進数に変換すると、11001010 となります。
Y
0 1 2 3 4 5 6 7 8 9 A B C D E F X 0 00 01 8D F6 CB 52 7B D1 E8 4F 29 C0 B0 E1 E5 C7 1 74 B4 AA 4B 99 2B 60 5F 58 3F FD CC FF 40 EE B2 2 3A 6E 5A F1 55 4D A8 C9 C1 0A 98 15 30 44 A2 C2 3 2C 45 92 6C F3 39 66 42 F2 35 20 6F 77 BB 59 19 4 1D FE 37 67 2D 31 F5 69 A7 64 AB 13 54 25 E9 09 5 ED 5C 05 CA 4C 24 87 BF 18 3E 22 F0 51 EC 61 17 6 16 5E AF D3 49 A6 36 43 F4 47 91 DF 33 93 21 3B 7 79 B7 97 85 10 B5 BA 3C B6 70 D0 06 A1 FA 81 82 8 83 7E 7F 80 96 73 BE 56 9B 9E 95 D9 F7 02 B9 A4 9 DE 6A 32 6D D8 8A 84 72 2A 14 9F 88 F9 DC 89 9A A FB 7C 2E C3 8F B8 65 48 26 C8 12 4A CE E7 D2 62 B 0C E0 1F EF 11 75 78 71 A5 8E 76 3D BD BC 86 57 C 0B 28 2F A3 DA D4 E4 0F A9 27 53 04 1B FC AC E6 D 7A 07 AE 63 C5 DB E2 EA 94 8B C4 D5 9D F8 90 6B E B1 0D D6 EB C6 0E CF AD 08 4E D7 E3 5D 50 1E B3 F 5B 23 38 34 68 46 03 8C DD 9C 7D A0 CD 1A 41 1C 表1 GF(28)の逆元テーブル
但し、ガロア体の性質は既約多項式で決定され、ここで用いられている既約多項式は以下で与えられます。
- 次に下記の行列変換を適用します。但し各係数の演算は2の1乗のガロア体GF(2)を想定するので、加算は排他的論理和EXORで計算されます。 00000000={00} は結果的に 01100011 = {63} に変換されます。
たとえば、{CA}= 11001010 を上記式に代入すると下記のようになり、
11101101 ={ED}に変換されます。
したがって、{53}は逆元計算で{CA}に変換され、行列計算により{ED}に変換されます。これがSubBytes変換となります。
逆SubBytes変換は上記の操作を逆に行う変換に対応しますので、以下の2つの変換を直列に並べた変換により実現できます。
- 行列の逆変換を行うのであるが、結果的に以下の行列変換式となります。
- そして、上記表1と同じ2の8乗のガロア体GF(28)の逆数に変換を行います。
したがって、SubBytes変換も逆SybBytes変換も同じ2の8乗のガロア体GF(28)の逆数計算を必要としています。
また、今回設計するのは切り替え信号により、SubBytes変換/逆SubBytes変換の機能切り替え可能な変換回路であるので、ガロア体の逆数回路を設計することで以下のようなアーキテクチャにより今回の設計課題を実現できることになります。
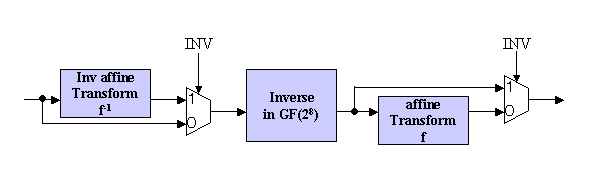
図2 課題アーキテクチャ例
INV信号が’0’の時は入力はガロア体の逆数計算回路に入り、その出力は行列変換計算回路に入り、逆にINV信号が’1’であれば、入力信号は先に行列の逆変換が計算され、その出力はガロア体の逆数計算回路に入力され逆数が計算されます。
行列計算は式からもわかるようにANDゲートとEXORゲートで実現できる単純な回路であるので、GF(28)の逆数計算をいかに巧くやるかがこの課題の設計のポイントとなります。以下にガロア体を簡単に説明します。
逆数計算を行うわけですが、結局のところ8ビット入力に対して表1に示される値を出力すればよく表をそのままHDLにて記述することにより逆数演算回路を実現することができます。
しかし、それではデザインコンテストで設計してもらうにはあまりにもつまらないので、1つの実装例を占めしておきます。
ある値 y の逆数 y-1 を求めるわけですが、GF(28)のガロア体の要素 y には
なる性質があります。したがって、
より、y254 を求めれば逆数が求まることになります。したがって、ガロア体の乗算器があればそれを繰り返し用いることで y254 を計算することができます。乗算器を多数用いた伊東・辻井による逆元演算回路の例を以下に示しておきます。
図3 伊東・辻井のアルゴリズムによる逆元計算回路
前のセクションで示したようにガロア体の乗算回路を繰り返し用いることで、逆元が計算できます。以下に、ガロア体の乗算回路の1つの実装例を示します。
ここで、2つの8ビットの数 A= (a7, a6, a5, a4, a3, a2, a1, a0)、B=(b7, b6, b5, b4, b3, b2, b1, b0) の乗算を考えます。2つの値は以下のような多項式で表すことができます。
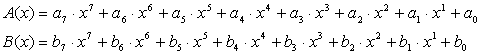
この多項式の乗算を行うと、
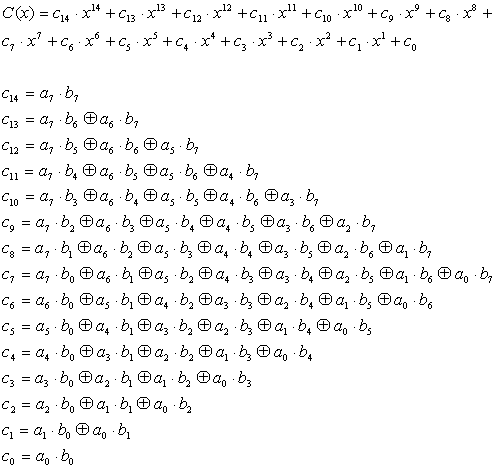
で与えられる14次の多項式となります。また各係数はGF(2)のガロア体の演算に従うので、乗算はAND演算、加算は排他的論理和EXOR演算となります。
ここで既約多項式=0とし、GF(2)では加算と減算は同じであるので、
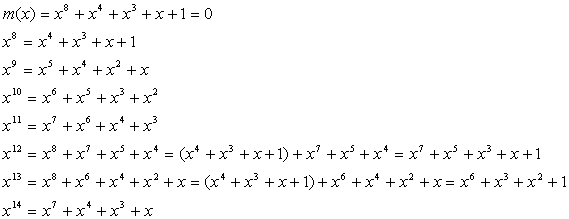
なる関係式を用いると上記C(X)は7次以下の多項式D(X)に変換することができます。
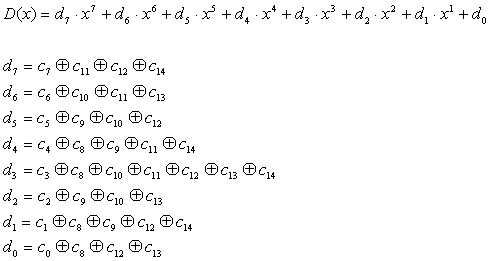
以上の計算により、2つの8ビットの数 A= (a7, a6, a5, a4, a3, a2, a1, a0)、B=(b7, b6, b5, b4, b3, b2, b1, b0) の乗算結果
D=(d7, d6, d5, d4, d3, d2, d1, d0) が得られます。
すなわち、実際の実装では多数のANDとEXORを用いることにより乗算器を実現することができます。
(注意)上記導出はデバッグをしてませんので、間違っている可能性はあります。
基本課題では以下の信号ビット幅とします。
|
SubBytes |
|||
| 信号名 | 入出力 | ビット幅 | 説明 |
| CLK | IN | 1 | クロック入力 |
| RESET | IN | 1 | ’1’でリセット |
| XIN | IN | 8 | 入力データ |
| INV | IN | 1 | ’0’でSubBytes変換、’1’で逆SubBytes変換 |
| YOUT | OUT | 8 | 変換されたデータ出力 |
表2 基本課題用ピンリスト
以下に送信機SENDER、ROMを用いて実装したSubBytes変換回路(SubBytesのみで逆SubBytesはできない)、全体シュミレーションのVHDLファイルをリンクします。必要に応じて修正して使用してください。
送信機: sender.vhd
SubBytes変換器: subbytes.vhd
全体テストベンチ: test_subbytes.vhd
以下にこのVHDLファイルを用いてシミュレーションを行った波形を示します。
SENDERが8ビットのPLAIN信号を出力し
その2サイクル遅れで、SUBBYTESがSubBytes変換値を出力しています。
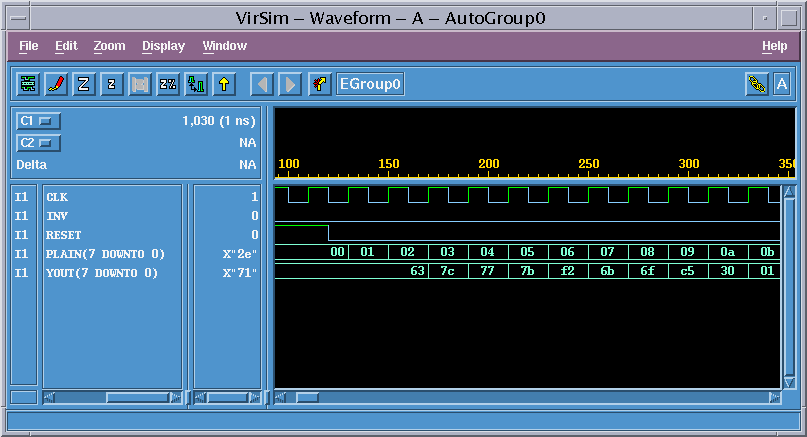
図4 シミュレーション波形
上記例では、SENDERが毎サイクル8ビットのPLAIN信号を出力していますが、回路削減のためにガロア体の乗算を複数サイクルかけて実行することも可能であり、必要に応じてPLAIN信号を数サイクルに1回出力するなど、自由に変更を行ってください。
LEVEL2では詳細な仕様は自由とします。
SubBytes変換と逆SubBytes変換ができればOKです。
琉球大学以外からの参加の場合、同一のシノプシスデザインコンパイラの論理合成用ライブラリを使用することが困難であるので、以下のような多段EXOR回路を例に従って合成し最適化して頂き、その1段あたりの遅延時間を単位時間としてスピードの単位とします。
多段EXOR回路のVHDLソース例:50入力のEXOR回路
この例では6段のEXOR段が合成され、クリティカルパス遅延はreport_timingコマンドにより7.17であったので、7.17/6=1.195を単位(UNIT)とします。
例えば、ある遅延が20ならば、20/1.195=17.74UNIT遅延とする。
琉大情報のライブラリ使用者は上記値で換算で換算すればよいです。
ちなみに面積はreport_areaコマンドのtotal cell areaにあります。
レポートには以下の内容を含めるてください。また、ページ数を少なめにコンパクトにまとめること。
| 表紙 | 1 | 代表者の氏名、チーム名、大学院修士/大学学部生/高専生の区別 |
| 2 | 共同設計者全員の名前(最高3名まで)、学籍番号、学年、学校名、住所、電話、email等連絡先 | |
| 3 | 全員のTシャツの希望サイズ | |
| 4 | 取り組んだ課題(LEVEL1/LEVEL2) | |
| 内容 | 1 | 設計した回路ブロックの構成説明(ブロック図と説明) |
| 2 | 設計した回路ブロックの動作説明(動作波形図やパイプライン動作等の説明) | |
| 3 | 工夫した点、オリジナリティを出した点(アピールが重要!) | |
| 4 | クリティカルパスのスピード、論理合成後の回路規模 | |
| 5 | VHDLもしくはVerilogのコード | |
| 6 | 正常動作しているVHDL/Verilogシミュレーション波形 | |
| 7 | その他自由意見など |
レポートはPDFファイルにて下記にEMAILにて提出すること!
他の形式での提出希望あれば、相談してください。
締め切りは2004年2月6日(金)必着です。
今回の課題を設計するのに非常に参考になる文献を紹介しておきます。
本LSI設計コンテストの学生部門の企画・実行、および沖縄での発表会は
主催:琉球大学工学部情報工学科
共催:株式会社沖縄産業振興センター
協賛: ソニーLSIデザイン株式会社
です。
ENJOY HDL! 沖縄で会おう!