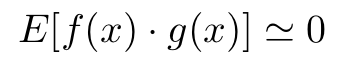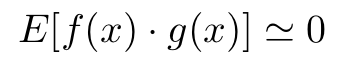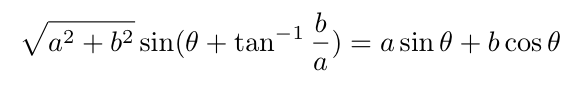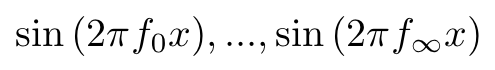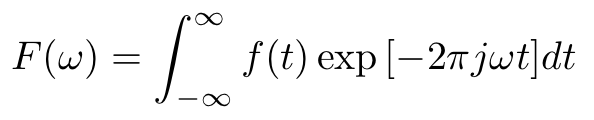フーリエ変換
これを読む前に、予備知識として以下の項目を熟読しておいて下さい。
直交基底関数
フーリエ変換は、ある関数をsinとcosの無限和で近似する際の、各周波数ごとの係数を求めるための変換である。
sin、cosの各周波数ごとの係数を求める事によって、周波数成分の分析に役立つ。
自己相関(Autocorrelation)の項で述べた通り、ある周期関数f(x)とg(x)があり、
それら二つの周期が異なれば、それらの関数の積の期待値は
となる。
f(x)とg(x)をそれぞれ三角関数として単純に考えれば非常に分かりやすい事と思う。
ただし、ここで、
とすれば、期待値は0になってしまう。
これはsinとcosが直交しているためであり、裏を返せばsinとcosを含む関数をg(x)とすれば、f(x)がどのような位相であろうとも期待値は0にはならないということである。関数が直交しているとは、まさに上記の式を満たす(正確には等号成立)ことであるが、簡単に述べれば「かけ算して積分をとれば0になる」ということである。
二次元の座標を表現するには、直交した二つの基底が必要であると言う事なのだが、例えば、2次元のデカルト座標は(x,y)のように、直交する二つの軸で空間の位置を全て記述出来るということである。
すなわち、三角関数の合成の公式
が示すように、任意に位相のずれた正弦波でもsinとcosの和で置き換える事ができるということを意味している。
つまり、sinとcosは直交基底関数であり、位相の情報を保持する事ができるということである。
ヒルベルト空間
次に、複数の異なる周波数を持つ三角関数を例にして、周波数の直交性を説明する。
上で述べた通り、関数f(x)とg(x)が直交であると言う事は、
を満たす事である。
ここで、f(x) = sin(2πx), g(x) = sin(4πx)としてその直交性を検証してみよう。
明らかに、期待値はゼロである(かけて積分するとゼロであるということ)。
このように、「二つの関数がともに正弦波であっても、周波数が違えば直交している」ということが言える。
もちろん、周波数の異なる正弦波
は、すべて直交している。(ただし、f_0は正の実数とする)
これで、我々は無限の直交基底関数を得た。このように、直交基底が無限に存在する空間を「ヒルベルト空間」とよぶ。
フーリエ変換
フーリエ変換とは何かを説明する前に、結論から述べる。
フーリエ変換とは、以下のようなヒルベルト空間への写像を行なう変換である。
f(t)を連続無限信号とすれば、
のようなF(ω)への写像をフーリエ変換という。
では、この式の意味を順を追って説明しよう。
オイラーの公式の項で説明したとおり、指数関数と三角関数は関係がある。その関係から、
であるから、以下のように変形するとF(ω)は複素数である事がわかる。
ここで、三角関数の合成の式を思い出してみよう。
sinとcosは直交基底関数なので、どのような位相の波であってもsinとcosの和でカバーできるというものであった。それらを考慮すると、フーリエ変換は位相を保持するためにsinとcosの両方の関数をそれぞれかけて面積を求め、直交性を検査しているということが分かる。
また、ωは周波数を表しており、フーリエ変換は無限に存在するの周波数から構成されるヒルベルト空間への写像を行なっているということがわかる。