21. 再帰関数¶
教科書4.3節。
21.1. 再帰関数とは¶
階乗を計算する関数について2つの実装を眺めてみよう。階乗関数とは、引数が1のときは1を返す。引数が2のときは2*1で2を返す。引数が3のときは \(3*2*1 = 6\) を返す。といった動作をする。つまり、引数が4ならば \(4*3*2*1 = 24\) を返すような関数だ。これまでの書き方であれば、for文もしくはwhile文を用いて、引数に合わせて1より大きな整数までを全て掛け合わせるようなコードを書くだろう。その例が左側のコード factl() だ。
これに対し、関数の中で自分自身を再帰的に呼び出す コード例 factR() を右に示している。ここに記述しているのは条件分岐とそれに伴うreturn文のみであり、2つ目のreturn文で自分自身 factR() を呼び出している。Stack frame を考えながら解読してみよう。
21.2. 実際の動作とスタックフレームの対応¶
factR 実行時のスタックフレームを書き出してみた。ここでは factR(3) を実行するものとし、この時点のスタックフレームを1番とする。
factRが呼び出されて内部に移動すると、新規にスタックフレーム2番「factR(3)」を生成する。このときの引数nは3であり、if文によりelseブロックが選択される。ここにはreturn文が記述されており「3 * factR(3-1)」、つまり「3 * factR(2)」を実行しようとする。factRは関数呼び出しのため新たにスタックフレームを呼び出してそこで処理を続ける。
factRが呼び出されて内部に移動すると、新規にスタックフレーム3番「factR(2)」を生成する。このときの引数nは2であり、if文によりelseブロックが選択される。ここにはreturn文が記述されており「2 * factR(2-1)」、つまり「2 * factR(1)」を実行しようとする。
factRが呼び出されて内部に移動すると、新規にスタックフレーム4番「factR(1)」を生成する。このときの引数nは1であり、if文によりTrueブロックが選択される。ここにはreturn文が記述されており「return 1」を実行する。ここで初めてスタックフレームの廃棄が始まり、スタックフレーム3番に戻る。
スタックフレーム3番「factR(2)」では「2 * factR(1)」の処理途中であった。factR(1)は1を返してきたため、2*1により2となり、これを返す。これによりスタックフレーム2番に戻る。
スタックフレーム2番「factR(3)」では「3 * factR(2)」の処理途中であった。factR(2)は2を返してきたため、3*2により6となり、これを返す。これによりスタックフレーム1番に戻る。
スタックフレーム1番は一番最初に「factR(3)」を呼び出した場所であり、先程の戻り値6が帰ってくる。
再帰関数の動作としては上記のとおりである。ではこれのどこが「類似したコード」なのだろうか。それは処理の手順にある。階乗関数ではnがどのぐらい大きくても「1まで遡って掛ける」という処理だ。これを「引数の値が1より大きいなら、1引いた値について同じ処理を実行しよう」という手順としてまとめたものが factR() となっている。
21.3. ループ処理 vs 再帰呼び出し¶
factRは、処理手順に共通点があることを利用して再帰関数として記述していた。このように「同じ構造」として処理手順を抽出できるなら、再帰関数としてシンプルに記述できることがある。シンプルに書けるということは読みやすいコードであり、潜在的なバグにも気づきやすくなる。一方で再帰関数にはデメリットもある。それはスタックフレームを積み上げている間は常にメモリを消費し続けているという点だ。あまりに膨大なスタックフレームを積み重ねると、StackOverFlowとなり、実行不可能となってしまうこともしばしばある。
21.4. 迷路探索の例¶
再帰関数の例をもう一つ紹介しよう。
maze_simple.py は、リストで用意された2次元格子空間を散策し、進むことができる空間を全て探索し尽くすためのプログラムである。探索方法にはいろいろあるが、例えば「現在地点から時計回りに確認。進めるなら先に進む。」ようにしてみよう。進める間は進み続けるため、後で戻ってきて未探索の場所を改めて探索し続ける必要がある。
上記に再帰関数として記述している主要部分を抜粋した。関数 walk_map_with_step_num は、現在地 map[y][x] について上右下左の順に移動可能かどうかを確認している。移動可能であればそこに移動し、改めて自分自身を呼び出すことで上右下左の順に処理を行う。つまり、移動可能ならばその都度スタックフレームを新規作成することでそれまでの状態を保存しておき、その後の処理をし終えたら(スタックフレームがここまで戻ってきたら)、その後の処理を継続することになる。
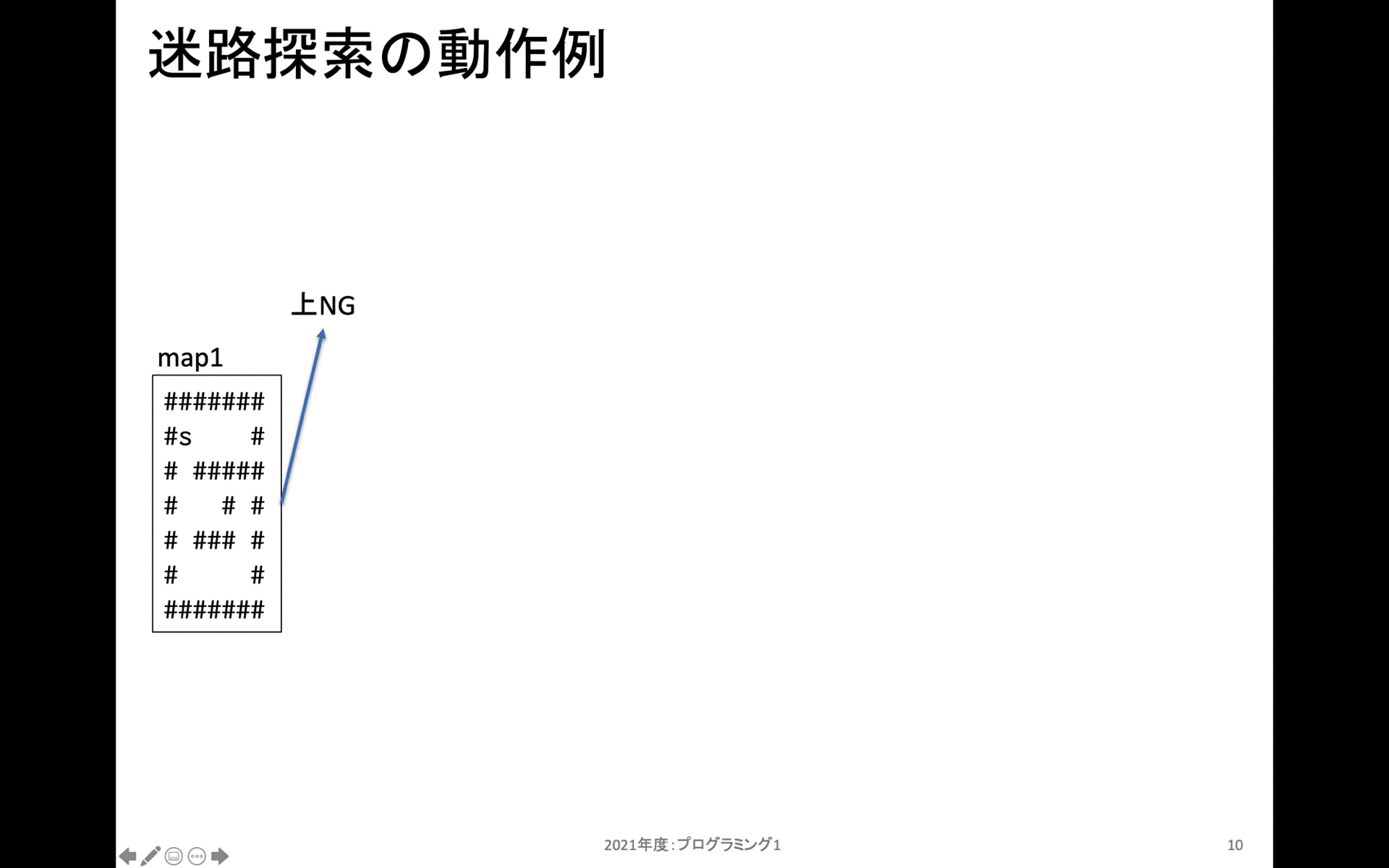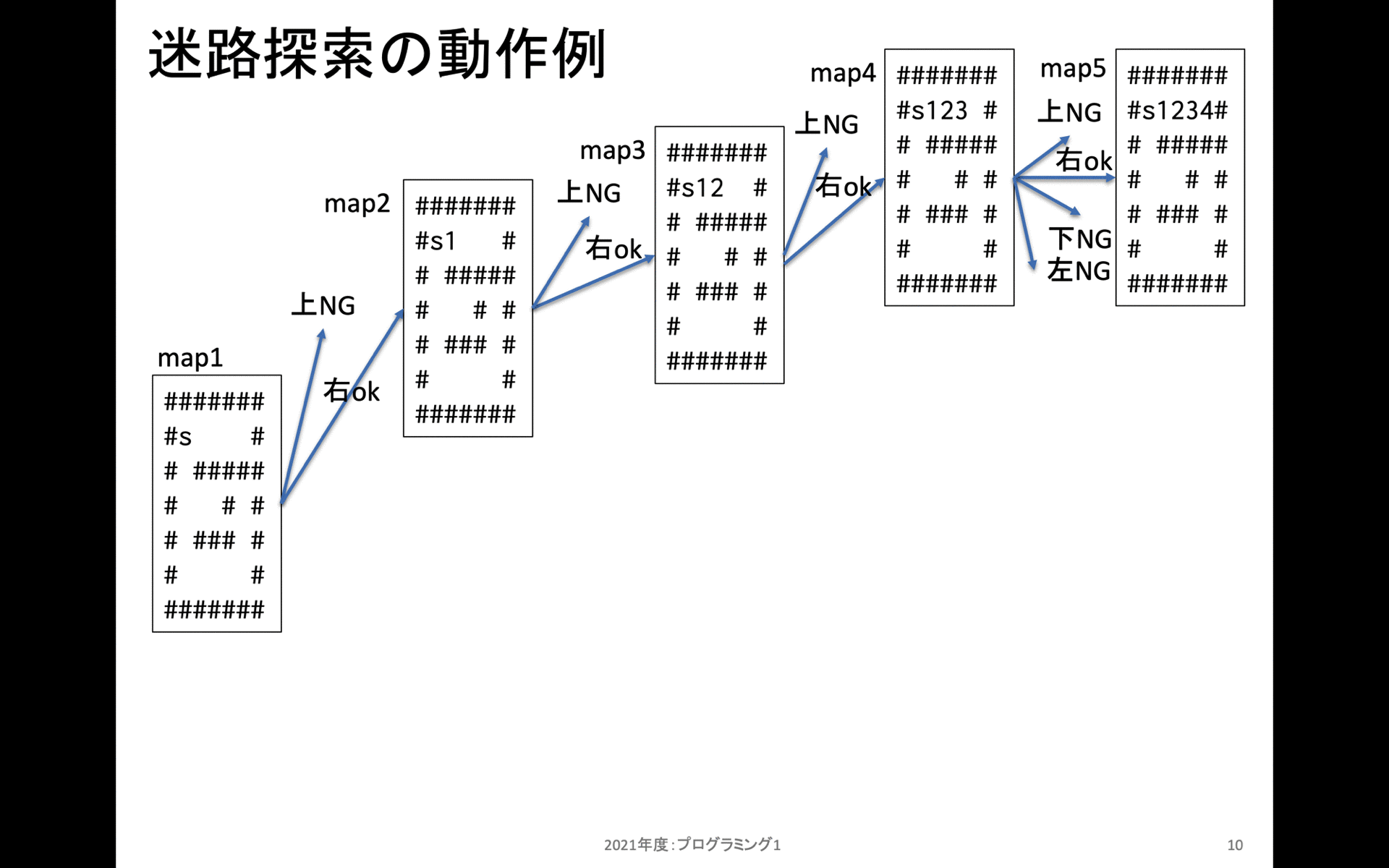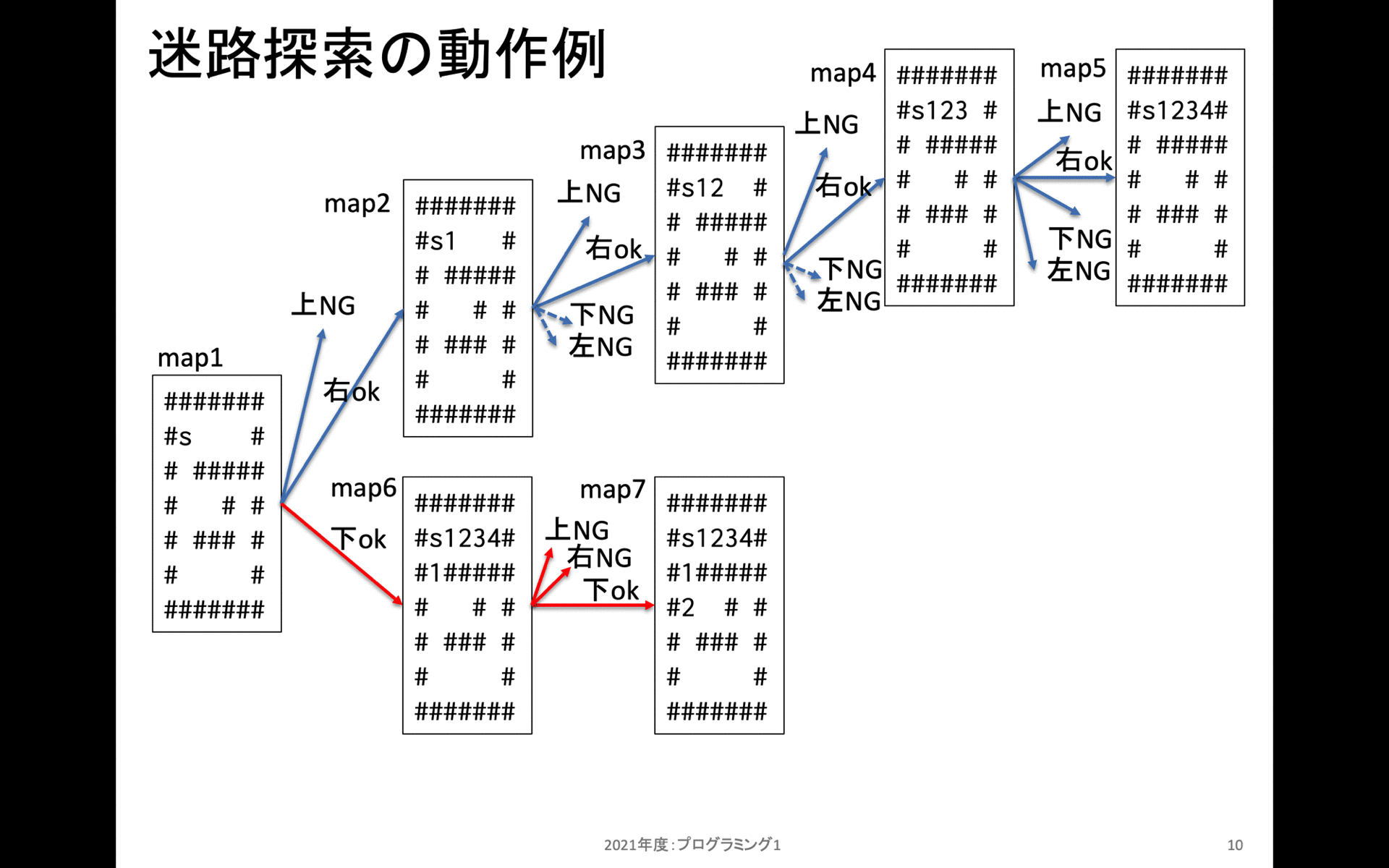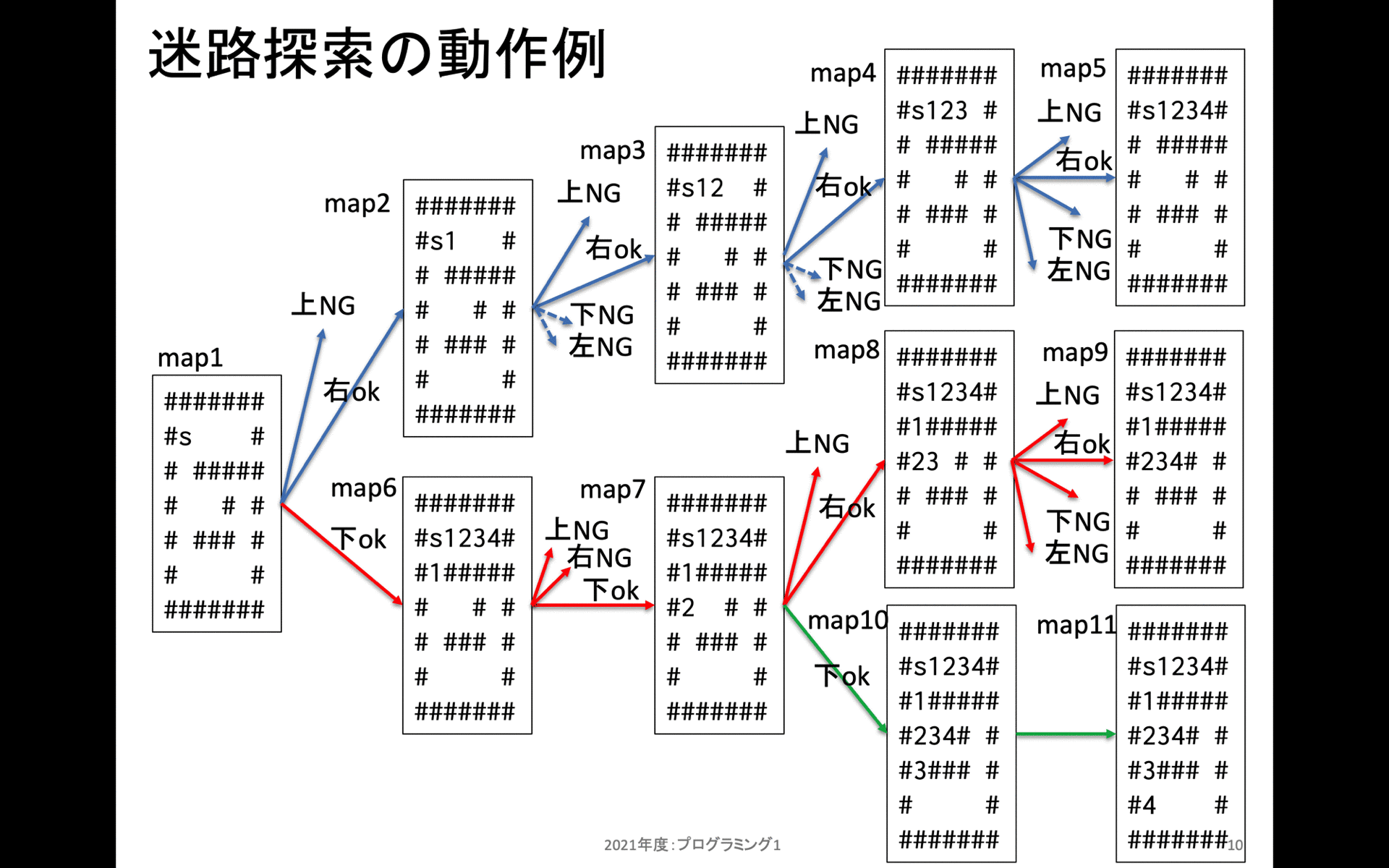
上記は walk_map_with_step_num の動作をスタックフレーム別に示している。一番最初は左側のmap1から始まる。map1の s がスタート地点だ。また # は移動できない場所だ。
map1の上には行くことができない。次に右方向には移動可能なので、右に移動してから新規にスタックフレームを作成する。
map2の上には行くことだけいない。次に右方向には移動可能なので、右に移動してから新規にスタックフレームを作成する。これを繰り返しmap5の状態までたどり着くと、上にも右にも下にも左にも移動することができない。(左は移動済みマーキングされているため、移動できないように処理している)。これでmap5のスタックフレームを処理し終えたので、この状態で一つ手前(map4)に戻る。
map4ではまだ上右の2箇所しか確認していなかったため、残り2箇所である下左を確認する。これらは移動できないため、この上阿智で一つ手前(map3)に戻る。
という具合に、全てのマスで「現在地点から時計回りに上右下左の順序で確認。進めるなら先に進む。」という処理を再帰処理として記述している。
21.5. 木構造¶
先程の考え方は木構造と呼ばれる構造を踏まえた探索方法である。全てのノードを処理するためにどの順番で処理していくか。それを深さ優先(先にすすめるならそこから処理する。処理し終えたら戻ってくる)という考え方で手順を整理した。
このように「類似したコード」における抽象化はとても難しい。抽象化した考え方はプログラミング1以外の授業も含めて少しずつ学んでいくため、今はそこまでやれる必要はない。プログラミング1としては、再帰関数の考え方を理解しよう。具体的には、再帰関数が出てきたとしても動作を理解できるようになろう。より詳しく確認したい場合には、maze_simple.py等のコード例を元に、breakpointを設定してデバッグ実行するといいだろう。