5. Example for Linear Regression#
story (Procedure of applied ML)
Preparation
Make the purpose (goal) clear.
Make the task concrete.
Check the possibilities to replace the existing services.
Prepare the dataset
Select a model
Continue learning, evaluation and tuning
ref.
# Prepare the dataset
# Load the diabetes dataset
# ref. https://scikit-learn.org/stable/datasets/index.html#diabetes-dataset
from sklearn import datasets
diabetes = datasets.load_diabetes()
orig_X = diabetes.data # get a feature matrix (input dataset)
print(type(orig_X)) # check the type
print(orig_X.shape) # check the size of feature matrix
print(orig_X[:5]) # display the first 5 samples
print(diabetes.feature_names) # display the name of each element of feature
<class 'numpy.ndarray'>
(442, 10)
[[ 0.03807591 0.05068012 0.06169621 0.02187235 -0.0442235 -0.03482076
-0.04340085 -0.00259226 0.01990842 -0.01764613]
[-0.00188202 -0.04464164 -0.05147406 -0.02632783 -0.00844872 -0.01916334
0.07441156 -0.03949338 -0.06832974 -0.09220405]
[ 0.08529891 0.05068012 0.04445121 -0.00567061 -0.04559945 -0.03419447
-0.03235593 -0.00259226 0.00286377 -0.02593034]
[-0.08906294 -0.04464164 -0.01159501 -0.03665645 0.01219057 0.02499059
-0.03603757 0.03430886 0.02269202 -0.00936191]
[ 0.00538306 -0.04464164 -0.03638469 0.02187235 0.00393485 0.01559614
0.00814208 -0.00259226 -0.03199144 -0.04664087]]
['age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6']
# convert np.ndarray to pd.dataframe for readability
import pandas as pd
df = pd.DataFrame(orig_X, columns=diabetes.feature_names)
df.head()
| age | sex | bmi | bp | s1 | s2 | s3 | s4 | s5 | s6 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.038076 | 0.050680 | 0.061696 | 0.021872 | -0.044223 | -0.034821 | -0.043401 | -0.002592 | 0.019908 | -0.017646 |
| 1 | -0.001882 | -0.044642 | -0.051474 | -0.026328 | -0.008449 | -0.019163 | 0.074412 | -0.039493 | -0.068330 | -0.092204 |
| 2 | 0.085299 | 0.050680 | 0.044451 | -0.005671 | -0.045599 | -0.034194 | -0.032356 | -0.002592 | 0.002864 | -0.025930 |
| 3 | -0.089063 | -0.044642 | -0.011595 | -0.036656 | 0.012191 | 0.024991 | -0.036038 | 0.034309 | 0.022692 | -0.009362 |
| 4 | 0.005383 | -0.044642 | -0.036385 | 0.021872 | 0.003935 | 0.015596 | 0.008142 | -0.002592 | -0.031991 | -0.046641 |
# Here, use just one feature 'bmi' for simple exercise
import numpy as np
X = diabetes.data[:, np.newaxis, 2]
print(X.shape)
print(X[:5])
(442, 1)
[[ 0.06169621]
[-0.05147406]
[ 0.04445121]
[-0.01159501]
[-0.03638469]]
y = diabetes.target
print(y.shape)
print(y[:5])
(442,)
[151. 75. 141. 206. 135.]
# split the dataset into training and testing set
num_of_training = 400
X_train = X[:num_of_training]
X_test = X[num_of_training:]
y_train = y[:num_of_training]
y_test = y[num_of_training:]
print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)
(400, 1)
(42, 1)
(400,)
(42,)
# Select a model
# => Linear Regression
from sklearn import linear_model
# Create linear regression object
regr = linear_model.LinearRegression()
# Train the model using the training set
regr.fit(X_train, y_train)
# Make predictions using the testing set
predicted = regr.predict(X_test)
# Check the predictions vs true answer
print(np.c_[predicted, y_test])
[[196.51241167 175. ]
[109.98667708 93. ]
[121.31742804 168. ]
[245.95568858 275. ]
[204.75295782 293. ]
[270.67732703 281. ]
[ 75.99442421 72. ]
[241.8354155 140. ]
[104.83633574 189. ]
[141.91879342 181. ]
[126.46776938 209. ]
[208.8732309 136. ]
[234.62493762 261. ]
[152.21947611 113. ]
[159.42995399 131. ]
[161.49009053 174. ]
[229.47459628 257. ]
[221.23405012 55. ]
[129.55797419 84. ]
[100.71606266 42. ]
[118.22722323 146. ]
[168.70056841 212. ]
[227.41445974 233. ]
[115.13701842 91. ]
[163.55022706 111. ]
[114.10695016 152. ]
[120.28735977 120. ]
[158.39988572 67. ]
[237.71514243 310. ]
[121.31742804 94. ]
[ 98.65592612 183. ]
[123.37756458 66. ]
[205.78302609 173. ]
[ 95.56572131 72. ]
[154.27961264 49. ]
[130.58804246 64. ]
[ 82.17483382 48. ]
[171.79077322 178. ]
[137.79852034 104. ]
[137.79852034 132. ]
[190.33200206 220. ]
[ 83.20490209 57. ]]
# Check the differences (errors)
print(y_test - predicted)
[ -21.51241167 -16.98667708 46.68257196 29.04431142 88.24704218
10.32267297 -3.99442421 -101.8354155 84.16366426 39.08120658
82.53223062 -72.8732309 26.37506238 -39.21947611 -28.42995399
12.50990947 27.52540372 -166.23405012 -45.55797419 -58.71606266
27.77277677 43.29943159 5.58554026 -24.13701842 -52.55022706
37.89304984 -0.28735977 -91.39988572 72.28485757 -27.31742804
84.34407388 -57.37756458 -32.78302609 -23.56572131 -105.27961264
-66.58804246 -34.17483382 6.20922678 -33.79852034 -5.79852034
29.66799794 -26.20490209]
# Check the sum of absolute error
print(sum(np.abs(y_test - predicted)))
# MAE (Mean Absolute Error)
print(sum(np.abs(y_test - predicted)) / len(X_test))
1890.1633693291935
45.00388974593318
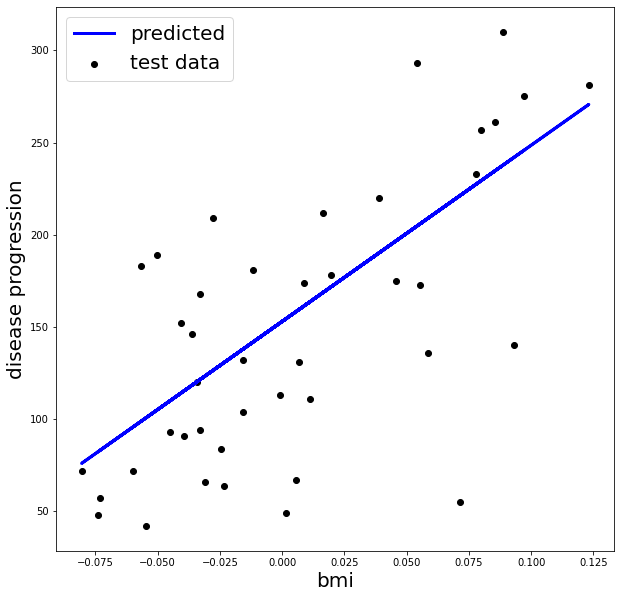
# Plot testing set and predictions
%matplotlib inline
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 1, figsize=(10, 10))
ax.scatter(X_test, y_test, color='black', label='test data')
ax.plot(X_test, predicted, color='blue', linewidth=3, label='predicted')
ax.legend(loc='best', fontsize=20)
ax.set_xlabel('bmi', fontsize=20)
ax.set_ylabel('disease progression', fontsize=20)
plt.show()
# Check the model (obtained parameters)
print('coefficients: ', regr.coef_)
print('intercept: ', regr.intercept_)
coefficients: [955.70303385]
intercept: 153.00018395675963