Example for Linear Regression
5. Example for Linear Regression¶
story (Procedure of applied ML)
Preparation
Make the purpose (goal) clear.
Make the task concrete.
Check the possibilities to replace the existing services.
Prepare the dataset
Select a model
Continue learning, evaluation and tuning
ref.
# Prepare the dataset
# Load the diabetes dataset
# ref. https://scikit-learn.org/stable/datasets/index.html#diabetes-dataset
from sklearn import datasets
diabetes = datasets.load_diabetes()
orig_X = diabetes.data # get a feature matrix (input dataset)
print(type(orig_X)) # check the type
print(orig_X.shape) # check the size of feature matrix
print(orig_X[:5]) # display the first 5 samples
print(diabetes.feature_names) # display the name of each element of feature
<class 'numpy.ndarray'>
(442, 10)
[[ 0.03807591 0.05068012 0.06169621 0.02187235 -0.0442235 -0.03482076
-0.04340085 -0.00259226 0.01990842 -0.01764613]
[-0.00188202 -0.04464164 -0.05147406 -0.02632783 -0.00844872 -0.01916334
0.07441156 -0.03949338 -0.06832974 -0.09220405]
[ 0.08529891 0.05068012 0.04445121 -0.00567061 -0.04559945 -0.03419447
-0.03235593 -0.00259226 0.00286377 -0.02593034]
[-0.08906294 -0.04464164 -0.01159501 -0.03665645 0.01219057 0.02499059
-0.03603757 0.03430886 0.02269202 -0.00936191]
[ 0.00538306 -0.04464164 -0.03638469 0.02187235 0.00393485 0.01559614
0.00814208 -0.00259226 -0.03199144 -0.04664087]]
['age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6']
# convert np.ndarray to pd.dataframe for readability
import pandas as pd
df = pd.DataFrame(orig_X, columns=diabetes.feature_names)
df.head()
| age | sex | bmi | bp | s1 | s2 | s3 | s4 | s5 | s6 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.038076 | 0.050680 | 0.061696 | 0.021872 | -0.044223 | -0.034821 | -0.043401 | -0.002592 | 0.019908 | -0.017646 |
| 1 | -0.001882 | -0.044642 | -0.051474 | -0.026328 | -0.008449 | -0.019163 | 0.074412 | -0.039493 | -0.068330 | -0.092204 |
| 2 | 0.085299 | 0.050680 | 0.044451 | -0.005671 | -0.045599 | -0.034194 | -0.032356 | -0.002592 | 0.002864 | -0.025930 |
| 3 | -0.089063 | -0.044642 | -0.011595 | -0.036656 | 0.012191 | 0.024991 | -0.036038 | 0.034309 | 0.022692 | -0.009362 |
| 4 | 0.005383 | -0.044642 | -0.036385 | 0.021872 | 0.003935 | 0.015596 | 0.008142 | -0.002592 | -0.031991 | -0.046641 |
# Here, use just one feature 'bmi' for simple exercise
import numpy as np
X = diabetes.data[:, np.newaxis, 2]
print(X.shape)
print(X[:5])
(442, 1)
[[ 0.06169621]
[-0.05147406]
[ 0.04445121]
[-0.01159501]
[-0.03638469]]
y = diabetes.target
print(y.shape)
print(y[:5])
(442,)
[151. 75. 141. 206. 135.]
# split the dataset into training and testing set
num_of_training = 400
X_train = X[:num_of_training]
X_test = X[num_of_training:]
y_train = y[:num_of_training]
y_test = y[num_of_training:]
print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)
(400, 1)
(42, 1)
(400,)
(42,)
# Select a model
# => Linear Regression
from sklearn import linear_model
# Create linear regression object
regr = linear_model.LinearRegression()
# Train the model using the training set
regr.fit(X_train, y_train)
# Make predictions using the testing set
predicted = regr.predict(X_test)
# Check the predictions vs true answer
print(np.c_[predicted, y_test])
[[196.51241167 175. ]
[109.98667708 93. ]
[121.31742804 168. ]
[245.95568858 275. ]
[204.75295782 293. ]
[270.67732703 281. ]
[ 75.99442421 72. ]
[241.8354155 140. ]
[104.83633574 189. ]
[141.91879342 181. ]
[126.46776938 209. ]
[208.8732309 136. ]
[234.62493762 261. ]
[152.21947611 113. ]
[159.42995399 131. ]
[161.49009053 174. ]
[229.47459628 257. ]
[221.23405012 55. ]
[129.55797419 84. ]
[100.71606266 42. ]
[118.22722323 146. ]
[168.70056841 212. ]
[227.41445974 233. ]
[115.13701842 91. ]
[163.55022706 111. ]
[114.10695016 152. ]
[120.28735977 120. ]
[158.39988572 67. ]
[237.71514243 310. ]
[121.31742804 94. ]
[ 98.65592612 183. ]
[123.37756458 66. ]
[205.78302609 173. ]
[ 95.56572131 72. ]
[154.27961264 49. ]
[130.58804246 64. ]
[ 82.17483382 48. ]
[171.79077322 178. ]
[137.79852034 104. ]
[137.79852034 132. ]
[190.33200206 220. ]
[ 83.20490209 57. ]]
# Check the differences (errors)
print(y_test - predicted)
[ -21.51241167 -16.98667708 46.68257196 29.04431142 88.24704218
10.32267297 -3.99442421 -101.8354155 84.16366426 39.08120658
82.53223062 -72.8732309 26.37506238 -39.21947611 -28.42995399
12.50990947 27.52540372 -166.23405012 -45.55797419 -58.71606266
27.77277677 43.29943159 5.58554026 -24.13701842 -52.55022706
37.89304984 -0.28735977 -91.39988572 72.28485757 -27.31742804
84.34407388 -57.37756458 -32.78302609 -23.56572131 -105.27961264
-66.58804246 -34.17483382 6.20922678 -33.79852034 -5.79852034
29.66799794 -26.20490209]
# Check the sum of absolute error
print(sum(np.abs(y_test - predicted)))
# MAE (Mean Absolute Error)
print(sum(np.abs(y_test - predicted)) / len(X_test))
1890.1633693291935
45.00388974593318
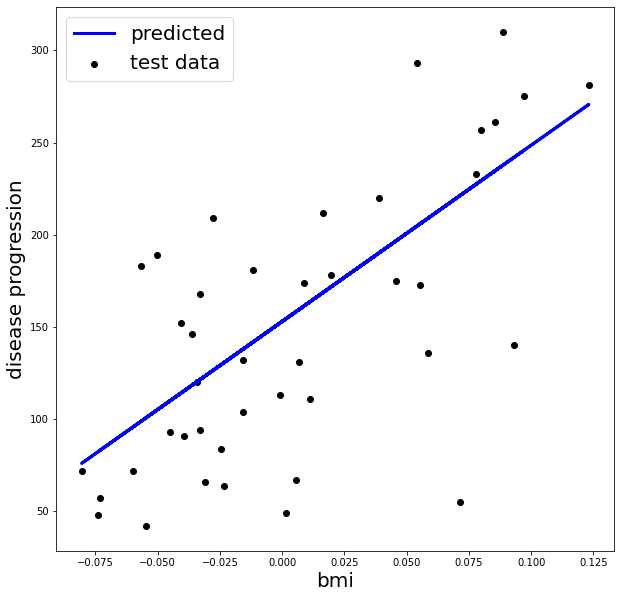
# Plot testing set and predictions
%matplotlib inline
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 1, figsize=(10, 10))
ax.scatter(X_test, y_test, color='black', label='test data')
ax.plot(X_test, predicted, color='blue', linewidth=3, label='predicted')
ax.legend(loc='best', fontsize=20)
ax.set_xlabel('bmi', fontsize=20)
ax.set_ylabel('disease progression', fontsize=20)
plt.show()
# Check the model (obtained parameters)
print('coefficients: ', regr.coef_)
print('intercept: ', regr.intercept_)
coefficients: [955.70303385]
intercept: 153.00018395675963